基于结构张量的图像修复

基于结构张量边缘强度模型的图像修复

摘要

在基于示例的图像修复方法中，通常存在两个主要问题：优先级计算不合理，以及块查找策略中仅考虑颜色特征。本文提出了一种基于结构张量边缘强度模型的图像修复方法。首先，我们采用渐进扫描修复方法，避免填充顺序受优先级函数的影响；然后，利用边缘强度模型构建块相似性函数，以正确识别局部图像结构；最后，使用平衡算子限制结构信息的过度传播，确保正确的结构重建。实验结果表明，我们的方法可与一些最先进的修复算法相媲美，甚至更优。

关键词 ：基于示例的技术，图像修复，结构张量，边缘强度模型，结构传播，平衡算子。

1 引言

图像恢复（即图像去噪、非盲去模糊和图像修复）[1]有助于恢复各种类型的图像。其中，图像修复是指利用图像中保留的可靠信息来恢复目标区域（缺失或损坏的部分）。修复技术依赖于图像中的颜色和结构信息，确保重建后的图像在视觉上合理。随着数字图像已成为我们生活的一部分，人们对图像的要求越来越高，例如修复因不当存储而受损的图像以及去除不必要的部分。该技术在视频和电影的后期处理中也发挥着重要作用，例如去除水印和恢复受损的老电影 [2, 3]。由于图像修复具有广泛的应用，这一技术已引起大量研究人员的关注，也是计算机视觉领域的一项重要任务。

近年来，图像修复取得了巨大进展，使用了基于偏微分方程（PDEs）、基于示例的技术以及基于稀疏表示的方法。偏微分方程图像修复算法[4]是一种基于热扩散的方法，其中曲率驱动扩散（CDD）模型[5]和全变分（TV）模型[6]是两种典型方法。李等人[7]提出了一种证明了TV算法，其中扩散系数的计算由目标区域内的像素与定义域内像素之间的距离和方向决定。然而，基于扩散的方法更适合修复无纹理区域，因为随着信息的扩散，纹理信息会被模糊。Yang等人[8]将结构张量应用于PDE算法以改进这一缺陷。基于偏微分方程的算法[4]的优点是能够处理小面积损伤区域（例如划痕）。对于大面积损伤区域或具有丰富结构信息的图像，该算法通常无法得到预期结果。因此，提出了一种基于范例的图像修复方法。在基于范例的图像修复算法中，确定图像边缘的修复顺序和块查找策略是通用步骤。这种修复方法擅长处理具有大面积损伤的图像。但是，基于范例的图像修复算法存在两个主要问题：优先级函数失效以及匹配块搜索策略不完整。针对这些问题，已提出了多种修复算法，并在[9]中介绍了这些算法的细节。Li等人[10]从置信项中减去一个常数，以避免优先级函数失效。Wang等人[11]通过引入正则化因子来调整优先级函数，提高了算法的鲁棒性，并采用结合改进的平方差之和（SSD）与归一化互相关（NCC）的方法来调整匹配块的搜索策略。Liu等人[12]利用结构张量构建局部度量函数以优化先验性和提出的匹配块搜索策略。方法在[12]有助于提高图像修复结果的结构保真度。在[13],中，匹配块的大小通过结构张量计算，更适用于各种纹理结构图像的修复。张等人[14]提出了一种基于非局部块张量的视觉数据补全算法，真实世界数据集上的实验结果表明该方法具有更优性能。此外，张量理论被广泛应用。其在目标识别中的应用见于1988[15]。矩阵半张量积被用于判断超网络化进化博弈（HNEG）是否具有势函数以及如何计算该势函数[16]。为了考虑图像的整体结构轮廓，部分文献[17]采用图像金字塔和Patch-Match算法[18]来解决图像中纹理与结构的正确重建问题。刘等人[19]将图像金字塔与克里米尼西算法相结合[20]，利用金字塔上层的修复结果指导下层的修复过程。该方法利用上层的修复结果改进优先级函数，从而获得更可靠的修复顺序。此外，研究发现图像的目标区域与已知区域之间存在相同的稀疏性，因此也出现了基于稀疏表示的修复方法[21, 22]。近年来，深度学习日益流行，在许多领域得到广泛应用，并取得了大量令人鼓舞的成果。姚等人[23]广泛介绍了深度学习在医疗保健中的应用。哈等人[1]综述了基于深度学习的模型和方法在单幅图像超分辨率任务中的最新进展。王等人[24]提出了一种针对大规模不规则掩码的图像修复方法。

在基于示例的图像修复算法中，修复质量受到边缘填充优先级和块查找策略的共同影响。随着填充的进行，数据项和置信项都会逐渐趋近于零，导致优先级函数失效。此外，块查找策略依赖单一的颜色特征来搜索匹配块。对于具有复杂纹理与结构的图像，容易在修复过程中匹配到错误的匹配块。因此，针对上述两个问题，无论其中哪一部分出现轻微误差，都会直接影响后续的填充效果。该算法的修复过程依赖于先前已填充的信息，当先前的修复出现错误时，后续的修复信息也会随之改变，从而在后续修复中引发连锁反应，导致结果不一致。此外，该算法还容易受到目标区域形状的影响，当所选目标区域发生微小变化时，边缘处的像素会发生显著变化。因此，本文提出一种基于结构张量边缘强度模型的图像修复技术，采用渐进扫描修复方法，以避免计算边缘填充块的优先级。当找到目标区域后，即开始搜索匹配块。为了准确识别图像中的结构信息，使用构建的边缘强度模型来搜索匹配块，以确保准确找到匹配块。提出的算法框架如图 1 所示。

2 相关工作

2.1 符号定义

如图2所示，Ω是源区域，Φ是目标区域，Ψx（以像素x为中心的方形块，大小为9×9像素）是扫描块，Ψp（大小为6×6像素）是待填充块。区域Ψz是与块Ψp相邻的源区域。如图2(a)所示，区域Ψz被分为两部分：A（块Ψp左侧的蓝色框）和B（块Ψp上方的绿色框）。当扫描块Ψx处于图2(b)状态时，块Ψx是待匹配块，块Ψy是最佳匹配块，块Ψq是最佳填充块。

在图2(c)中，ĥ是整个目标区域Φ的长度，ŵ是整个目标区域Φ的宽度，h是块底部到目标区域Φ下边界的距离，w是块Ψx右侧到目标区域Φ右边界的距离。令ĥ - h为值Lh，令ŵ - w为值Lw。待填充块Ψp左侧和上方相邻的方形块分别记为ΨA_p和ΨB_p（大小为6×6像素）。

2.2 边缘强度模型

为了定义结构张量，设图像的梯度为
∇I = [Ix, Iy]^T (1)
其中，Ix 和 Iy 分别是像素在x方向和y方向上的偏导。

图像的结构张量E可定义为
E = ∇I∇I^T = [Ix², IxIy; IxIy, Iy²] (2)

E是一个对称的二维半正定矩阵，它具有两个非负特征值λ₁和λ₂。边缘强度使用λ₁和λ₂来定义图像数据的一致性。像素处的边缘强度为
H(i, j) = (λ₁ - λ₂)² (3)

特征值λ₁和λ₂可用于分析局部图像结构。当两个特征值都接近零时，表示灰度值在各个方向上的变化很小，它们位于平坦区域。当一个特征值远大于另一个特征值（趋近于零）时，表示图像具有明显的边缘结构。当两个特征值均大于零且其中一个特征值远大于另一个时，表示存在角点区域。

在传统的基于范例的图像修复算法中，仅使用颜色特征来搜索匹配块。因此，无法正确识别目标区域周围的结构信息。如图3所示，待匹配块Ψx的源区域已经存在直线结构和部分角点结构。如果仅使用单一的颜色特征来寻找最佳匹配块，则容易遗漏待匹配块Ψx附近的角点信息。因此，会找到错误的匹配块Ψy₂，而错过正确的匹配块Ψy₁。结果，直线结构被修复，但角点信息丢失，导致图像修复失败。

结构张量能够识别图像中不同纹理结构的特征。通过计算块Ψx和Ψy（由中心像素y(i, j)处的边缘强度表示）以及块Ψx和Ψy的边缘强度x(i, j)，提高了识别目标图像中结构信息的准确性。这两个边缘强度分别记为H(iy, jy)和H(ix, jx)。为了判断待匹配块与匹配块Ψy之间的相干性，构建了图像的边缘强度模型：
H(x, y) = (H(ix, jx) + H(iy, jy)) / 2 × ω (4)
其中ω是一个常数（ω = 0.001）。从(3)式及结构张量特征值的特性可知，当H(x, y)的值趋近于零或等于零时，意味着Ψx和Ψy的相干性较低，且像素位于平坦区域。如果H(x, y)的值远大于零，则表示Ψx和Ψy具有高度相干性，且像素周围存在结构信息。

3 算法

基于示例的图像修复方法通常存在两个主要问题：优先级函数容易失效，以及块查找策略不够完善。本文提出了一种基于结构张量边缘强度模型方法的图像修复技术。其实现步骤如下。

3.1 渐进扫描

在基于示例的图像修复算法中，优先级由数据项和置信项的乘积决定。然而，随着填充的进行，数据项和置信项都会逐渐接近零，导致优先级函数失效。结果，无法确定边缘填充的顺序，容易引起填充误差。

为了避免受到优先级函数的影响，该算法在修复过程中采用渐进扫描方法。算法使用扫描块Ψx对图像进行渐进式扫描，每次移动一个像素长度。当扫描块Ψx找到目标区域Φ时，继续移动扫描块Ψx，直到Ψx和Φ具有最大的重合区域。

当满足(5)时，便开始搜索匹配块。
Ψz ∩ Φ = ∅ (5)

3.2 准确识别局部结构信息

传统上仅考虑单一颜色特征的一种块查找策略。它忽略了图像的结构信息。本文引入边缘强度模型来识别局部图像结构特征。块相似性函数定义为
D(Ψx, Ψy) = D(Ψx, Ψy) + α × H(x, y) (6)
其中，α为强度调整因子（经验值α = 10），H(x, y)为待匹配块Ψx与匹配块Ψy之间的边缘强度，D(Ψx, Ψy)表示为
D(Ψx, Ψy) = Σ√((RΨx - RΨy)² + (GΨx - GΨy)² + (BΨx - BΨy)²) (7)
D(Ψx, Ψy)是源区域中每个块Ψy与块Ψx之间的SSD距离，其中R、G和B代表各通道对应的像素值。

Ψx在本文中，扫描块还为边缘强度的计算提供了H(ix, jx)基础。在图2(b)中，区域Ψz包含更多可靠信息，能够准确识别待填充块周围的纹理与结构Ψp，然后根据(6)在整个图像中搜索最佳匹配块Ψy。为了提高匹配块的准确性，定义了一种过滤策略为
Ψŷ < arg min_{Ψy ∈ Ω} D(Ψx, Ψy) × err (8)
其中err是待匹配块Ψx与匹配块Ψy之间的相似度，err = λ + β × H(ix, jx)为误差调整因子，λ = 1.3，β = 10为经验值，H(ix, jx)是待匹配块Ψx的边缘强度。

过滤后，匹配的块可能存在三种情况Ψy。区域Ψz被划分为两个区域A和B（如图2(a)所示）。

1) 匹配块Ψy与对应的区域A和区域B的图像信息相匹配，则该匹配块为具有最佳填充性能的最佳匹配块。
2) 匹配块Ψy与对应区域A或区域B的图像信息相匹配，因此其中一些具有可靠的填充信息。
3) 匹配块Ψy与对应区域A和区域B的部分图像信息匹配，但并非全部完全匹配。

如果在1)中不存在经过滤波的匹配块Ψy，则需要从2)和3)中进一步匹配最佳匹配块。通过分析，如果两个匹配块之间存在匹配差异，则这两个区域之一将包含结构信息。这表明区域A和B的图像信息（如图2(a)）所示，应具有较大的差异。结构信息是图像信息的骨架，因此在这两个区域中优先选择具有结构信息的方向进行修复。

3.3 平衡因子

如果允许结构信息过度传播，则修复将失败。因此，我们定义一个平衡因子来限制结构的过度扩展。该平衡因子基于图像梯度和图像修复程度。首先确定当前目标区域的Φ修复程度如图2(c)所示，计算待匹配块Ψx在垂直和水平方向上的修复程度。设Lh和Lw分别表示待匹配块Ψx在这两个方向上的修复程度。记Ψp的相邻块（如图2(c)所示）的梯度模值分别为|I|A和|I|B。梯度模值越大，图像中包含的结构信息越强。因此，优先修复结构信息较强的区域。

平衡因子决定了待匹配块Ψx进行优先匹配的方向。如图2(a)所示，它根据区域A或区域B中的匹配信息进行优先匹配。平衡因子可表示为
V = |I| / L (9)
其中|I|为|I|A或|I|B，L为Lh或Lw。

最后，使用(7)计算图2(c)中Ψq的ΨA_p或ΨB_p（A或B）与已填充块之间的SSD距离。将这些距离的平均值作为平均值Ave：
Ave = Σ_{i=1}^{n} D(Ψr_p, Ψq) / n (10)
其中n为匹配块的总数（由公式(8)筛选出的匹配块）。两个块之间的距离越大，其相似性越小；距离越小，相似性越高。因此，在距离小于平均值Ave的候选块中，我们选择与块Ψp最相似的匹配块作为最佳填充块Ψq，以及块Ψq中的像素被复制到块Ψp的对应位置。

本文算法的伪代码如算法1所示。图4展示了Sill在图像修复过程中四组匹配块的搜索过程。在图4(a)状态1中，白色块表示经过公式(8)过滤后剩余的匹配块。在图4(b)状态2中，蓝色块表示利用平衡因子V对白色匹配块进一步过滤的结果。在图4(c)状态3中，红色块为最佳匹配块。从这四组匹配块搜索过程图可以看出，无论是在平坦区域还是结构区域，匹配块的搜索都是正确的，表明我们的搜索策略在寻找最佳匹配块方面是有效的。Sill的完整图像修复过程见动画（在线资源1）。

算法1. 基于结构张量边缘强度模型的图像修复

输入：目标图像，标记颜色
输出：修复后的图像

1) 使用9×9扫描块Ψx作为基本块进行扫描。从上到下、从左到右逐步扫描目标图像，当扫描块Ψx找到目标区域Φ时，继续移动扫描块Ψx；
2) while Ψz ∩ Φ = ∅ do
i) 使用patch similarity(6)对图像进行全局搜索，并为待匹配块Ψx搜索匹配块；
ii) 使用(8)过滤步骤i）中的匹配块；
iii) 通过计算待匹配块Ψx的平衡因子V来确定优先匹配方向；
iv) 使用(7)计算块ΨA_p或ΨB_p填充块Ψq之间的SSD距离，并使用(10)对这些距离进行平均；
v) 在距离小于平均值Ave的匹配块中，与待填充块Ψp最相似的匹配块即为最佳填充块Ψq。然后，将最佳填充块Ψq中的像素相应地复制到待填充块Ψp的对应位置。
3) end while
4) 重复上述步骤，直到图像被修复完成。

4 实验结果

视觉感知通常用于评估图像修复的结果。此外，还可以通过结构相似性指数度量（SSIM）、峰值信噪比（PSNR）值以及图像修复所需时间来加以说明。该算法通过与 [20]、[11] 和 [10] 中的方法进行比较，验证了本文实验的有效性。

为了测试我们的方法，我们检查了它在各种场景图像中的修复能力，如图5−8所示。其中，(a)列是目标图像，(b)、(c)和(d)列分别是[20]、[11]和[10]这些方法的修复结果，而(e)列是我们的方法的修复结果。

4.1 受损图像修复

图5和图6显示了受损图像的修复结果，分别为围栏、窗户、楼梯、岛屿、山和高速公路图像。

在图5中，存在一些具有复杂纹理和结构的图像。在图5(b)−5(d)中，我们可以看到方法在[20]、[11]和[10]中的结果显示出错误的信息。这是因为未能考虑图像结构周围的特征，导致修复失败。例如，在围栏和窗户图像的修复中，[20]和[11]的方法破坏了线性结构和交叉结构。而[10]的方法无法恢复围栏和楼梯的线性结构，但重建了窗户的交叉结构。在楼梯的修复中，[20]和[10]的方法在重建台阶的线性结构时是不正确的。

然而，我们的方法恢复了围栏、窗户和楼梯图像中的错误结构。

有三幅场景图像在图6中。在对岛屿和山的图像进行修复时，[20]中的方法将错误信息复制到了天空区域，而[11]和[10]中的方法在重建树木和山脉时出现错误。在这种情况 下，我们的方法能够重建树木和天空。我们的方法以及[20]、[11]和[10]中的方法在高速公路图像的修复中取得了良好结果。

表1和表2是对上述六组实验使用峰值信噪比和结构相似性指标进行的实验评估。这两个指标可以反映不同方法的修复效果。结果表明，我们的方法在[20]、[11]和[10]方面优于其他方法。

4.2 物体移除

移除物体后的修复图像如图7和图8所示。这些是使用高纹理不规则图案进行修复的图像，分别为女孩、女人、狐狸、人物、游客和船的图像。物体移除是指去除图像中的额外物体，即女孩和女人图像中的人物，狐狸躺在木头上，人物和汽车分别位于人物和游客图像中，以及船图像中的航行中的船。

表3列出了几种方法的时间对比。从表3可以看出，与[20]、[11]和[10]中的三种方法相比，我们的方法不仅可以节省修复时间，而且还能确保修复结果满足视觉要求。

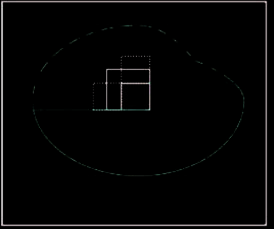
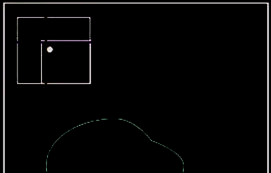
表1 峰值信噪比不同算法对图像修复的性能比较（dB）

图像（尺寸）	方法在[20]	方法在[11]	方法在[10]	我们的方法
围栏 (227×227)	26.4567	27.4238	27.9668	33.6871
窗户 (202×256)	32.4223	31.8532	34.8220	38.1820
楼梯 (392×258)	30.8778	32.3194	29.9823	32.9061
岛屿 (128×128)	23.3554	25.6930	26.4080	30.1055
山 (300×200)	22.1677	21.9778	25.6218	27.9696
高速公路 (240×212)	30.8553	30.6990	29.8945	31.6898

表2 结构相似性不同算法对修复图像的性能比较

图像（尺寸）	方法在[20]	方法在[11]	方法在[10]	我们的方法
围栏 (227×227)	0.8843	0.8426	0.8739	0.9026
窗户 (202×256)	0.9201	0.9059	0.9319	0.9468
楼梯 (392×258)	0.9139	0.9221	0.9066	0.9280
岛屿 (128×128)	0.8444	0.8568	0.8788	0.8879
山 (300×200)	0.8102	0.7875	0.8547	0.8592
高速公路 (240×212)	0.8446	0.8401	0.8290	0.8545

表3 图像（尺寸）恢复时间由不同方法（s）

图像（尺寸）	方法在[20]	方法在[11]	方法在[10]	我们的方法
围栏 (227×227)	41.1230	695.4319	43.5683	40.5685
窗户 (202×256)	12.3578	139.3616	13.0398	12.2736
楼梯 (392×258)	15.1306	272.1375	17.8500	14.1943
岛屿 (128×128)	15.2993	112.6544	15.8441	14.0476
山 (300×200)	38.9698	540.8811	50.8185	36.0710
高速公路 (240×212)	35.1901	758.2118	45.1673	34.0085
女孩 (384×256)	54.5084	1861.6	66.0055	43.5231
女人 (128×128)	8.6212	71.90.85	9.2783	8.3218
狐狸 (128×128)	4.8411	42.8257	4.7980	4.7057
人物 (128×128)	4.8405	34.4488	4.9118	4.6854
游客 (240×180)	21.7440	371.8106	22.0711	20.6946
船 (128×128)	10.8383	62.3569	11.7175	10.1854

5 结论

本文提出了一种基于结构张量边缘强度模型的图像修复算法。该算法采用渐进扫描方法，以避免边缘填充顺序受到优先级函数的影响。在块查找策略中引入了边缘强度模型。同时，结合了结构信息和颜色信息。在图像的匹配块选择中考虑了这些区域，以确保匹配块的正确性。该算法的有效性通过在Matlab中进行的多次仿真实验得以验证。我们的实验是在Intel核心i5 CPU @ 1.6GHz上进行的。

对于受损图像的重建和物体去除，修复结果是视觉上合理的。此外，采用峰值信噪比和结构相似性指标与不同算法进行比较。实验表明，我们提出的算法在不同类型结构的图像修复中表现令人满意。此外，通过比较几种算法的修复时间，也说明了我们的算法具有高效率。