最短路径-Dijkstra

原创于 2024-09-27 21:15:11 发布 · 1.1k 阅读

23 ·

CC 4.0 BY-SA版权

文章标签：

#算法

算法设计

解决2个问题

如何存放最短路径长度:

用一维数组dist[j]存储!源点v默认， dist[j]表示源点中顶点j的最短路径长度。如dist[2]=12表示源点中顶点2的最短路径长度为12。

如何存放最短路径:

从源点到其他顶点的最短路径有n-1条，一条最短路径用一个一维数组表示，如从顶点0中5的最短路径为0、2、3、5.表示为

path[5]={0,2.3,5}.

所有n-1条最短路径可以用二维数组path[]存储。

例：

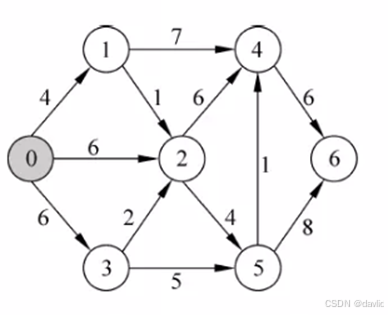
转为矩阵形式

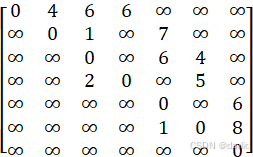
手工计算过程：

Path表示：存放最短路径顶点-1 表示源点0到顶点i没有路径0 从源点0的最短路径，且最短路径上顶点i的前一个顶点是源点0，即path[0]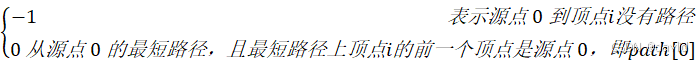

计算过程

- 初始化：S{0},U={1,2,3,4,5,6}

dist={0,4,6,6,∞,∞,∞}path[]={0,0,0,0,-1,-1,-1}

- U 找到最小顶点1（权重最小），加入s{0,1}, U={2,3,4,5,6},顶点1出发有2，4顶点，

dis2=mindis2,dis1+1=min6,5=5dis4=mindis4,dis1+7=min4+7,6+6=11

修改

dis=[{0,4,5,6,11,∞,∞}]

path[]={0,,0,1,0,1,-1,-1}

- U 找到最小顶点2（权重最小），加入s{0,1,2}, U={3,4,5,6},顶点2出发有4,5顶点，

dis4=mindis4,dis2+6=min11,5+6=11dis5=mindis5,dis2+4=min9,5+4=9

修改

dis=[{0,4,5,6,11,9,∞}]

用顶点2代替

path[]={0,,0,1,0,1,2,-1}

- U 找到最小顶点3，加入s{0,1,2,3}, U={4,5,6},顶点3出发有2,5顶点，

dis2 考查过，不必修改dis5=mindis5,dis3+5=min9,6+5=9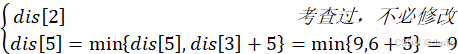

修改

dis=[{0,4,5,6,11,9,∞} 没有修改

path[]={0,,0,1,0,1,2,-1} 没有修改

- U 找到最小顶点5（权重最小），加入s{0,1,2,3,5}, U={4,6},顶点5出发有4,6顶点，

dis4=mindis4,dis5+1=11,10=10 dis6=mindis6,dis5+8=min4+1+4+8,9+8=17

修改

dis={0,4,5,6,10,9,17}

path[]={0,,0,1,0,5,2,5}

- U 找到最小顶点4（权重最小），加入s{0,1,2,3,5,4}, U={6},顶点4出发有6顶点，

dis6=mindis6,dis4+6=min17,10+6=16

修改

dis={0,4,5,6,10,9,16}

path[]={0,,0,1,0,5,2,4}

- U 找到最小顶点6（权重最小），加入s{0,1,2,3,5,4,6}, U={},顶点6出发没有任何顶点S包括路径，

dis={0,4,5,6,10,9,16}

path[]={0,,0,1,0,5,2,4}

- 找出最短路径：16

Path[6]=4, Path[4]=5, Path[5]=2, Path[2]=1, Path[1]=0

反推最短路径：0→1→2→5→4→6

代码（java)

public class DijkstraAlgorithm {

    private static final int MAXV = 7;
    private static final int INF = Integer.MAX_VALUE / 2;

    public static void main(String[] args) {
        MatGraph g = new MatGraph(MAXV);
        g.edges = new int[MAXV][MAXV];

        // 初始化图
        g.edges[0][1] = 4;
        g.edges[0][2] = 6;
        g.edges[0][3] = 6;
        g.edges[0][4] = INF;
g.edges[0][5] = INF;
        g.edges[0][6] = INF;

        g.edges[1][0] = INF;
        g.edges[1][1] = 0;
        g.edges[1][2] = 1;
        g.edges[1][3] = INF;
        g.edges[1][4] = 7;
        g.edges[1][5] = INF;
        g.edges[1][6] = INF;

        g.edges[2][0] = INF;
        g.edges[2][1] = INF;
        g.edges[2][2] = 0;
        g.edges[2][3] = INF;
        g.edges[2][4] = 6;
        g.edges[2][5] = 4;
        g.edges[2][6] = INF;

        g.edges[3][0] = INF;
        g.edges[3][1] = INF;
        g.edges[3][2] = 2;
        g.edges[3][3] = 0;
        g.edges[3][4] = INF;
        g.edges[3][5] = 5;
        g.edges[3][6] = INF;

        g.edges[4][0] = INF;
        g.edges[4][1] = INF;
        g.edges[4][2] = INF;
        g.edges[4][3] = INF;
        g.edges[4][4] = 0;
        g.edges[4][5] = INF;
        g.edges[4][6] = 6;

        g.edges[5][0] = INF;
        g.edges[5][1] = INF;
        g.edges[5][2] = INF;
        g.edges[5][3] = INF;
        g.edges[5][4] = 1;
        g.edges[5][5] = 0;
        g.edges[5][6] = 8;

        g.edges[6][0] = INF;
        g.edges[6][1] = INF;
        g.edges[6][2] = INF;
        g.edges[6][3] = INF;
        g.edges[6][4] = INF;
        g.edges[6][5] = INF;
        g.edges[6][6] = 0;

        // 对角线元素设为0
        for (int i = 0; i < MAXV; i++) {
            g.edges[i][i] = 0;
        }

        // 其他位置设为INF
        for (int i = 0; i < MAXV; i++) {
            for (int j = 0; j < MAXV; j++) {
                if (g.edges[i][j] == 0 && i != j) {
                    g.edges[i][j] = INF;
                }
            }
        }

        int v = 0; // 源点
        int[] dist = new int[MAXV];
        int[] path = new int[MAXV];
        boolean[] S = new boolean[MAXV];

        Dijkstra(g, v, dist, path, S);
        Dispath(g, dist, path, S, v);
    }

    public static void Dijkstra(MatGraph g, int v, int[] dist, int[] path, boolean[] S) {
        for (int i = 0; i < g.n; i++) {
            dist[i] = g.edges[v][i];
            S[i] = false;
            if (g.edges[v][i] < INF) {
                path[i] = v;
            } else {
                path[i] = -1;
            }
        }
        S[v] = true;
        path[v] = 0;

 for (int i = 0; i < g.n - 1; i++) {
            int u = findMinDistanceVertex(dist, S);
            S[u] = true;

            for (int j = 0; j < g.n; j++) {
                if (!S[j] && g.edges[u][j] < INF && dist[u] + g.edges[u][j] < dist[j]) {
                    dist[j] = dist[u] + g.edges[u][j];
                    path[j] = u;
                }
            }
        }
    }

    private static int findMinDistanceVertex(int[] dist, boolean[] S) {
        int minDistance = INF;
        int minIndex = -1;
        for (int j = 0; j < dist.length; j++) {
            if (!S[j] && dist[j] <= minDistance) {
                minDistance = dist[j];
                minIndex = j;
            }
        }
        return minIndex;
    }

    public static void Dispath(MatGraph g, int[] dist, int[] path, boolean[] S, int v) {
        for (int i = 0; i < g.n; i++) {
            if (S[i] && i != v) {
                System.out.printf("从顶点%d 到顶点%d 的路径长度为: %d 路径为: ", v, i, dist[i]);
                printPath(path, v, i);
            }
        }
    }

    private static void printPath(int[] path, int v, int i) {
        if (path[i] == -1) {
            System.out.println("无路径");
            return;
        }
        int[] apath = new int[MAXV];
int d = 0;
        apath[d++] = i;
        int k = path[i];
        while (k != v) {
            apath[d++] = k;
            k = path[k];
        }
        apath[d++] = v;

        System.out.print(apath[d - 1]);
        for (int j = d - 2; j >= 0; j--) {
            System.out.print(" -> " + apath[j]);
        }
        System.out.println();
    }

    static class MatGraph {
        int n;
        int[][] edges;

        public MatGraph(int n) {
            this.n = n;
        }
    }
}

结果：

*从顶点0 到顶点1 的路径长度为: 4 路径为: 0 -> 1
* 从顶点0 到顶点2 的路径长度为: 5 路径为: 0 -> 1 -> 2
* 从顶点0 到顶点3 的路径长度为: 6 路径为: 0 -> 3
* 从顶点0 到顶点4 的路径长度为: 10 路径为: 0 -> 1 -> 2 -> 5 -> 4
* 从顶点0 到顶点5 的路径长度为: 9 路径为: 0 -> 1 -> 2 -> 5
* 从顶点0 到顶点6 的路径长度为: 16 路径为: 0 -> 1 -> 2 -> 5 -> 4 -> 6