6.10.单源最短路径问题-Dijkstra算法

---

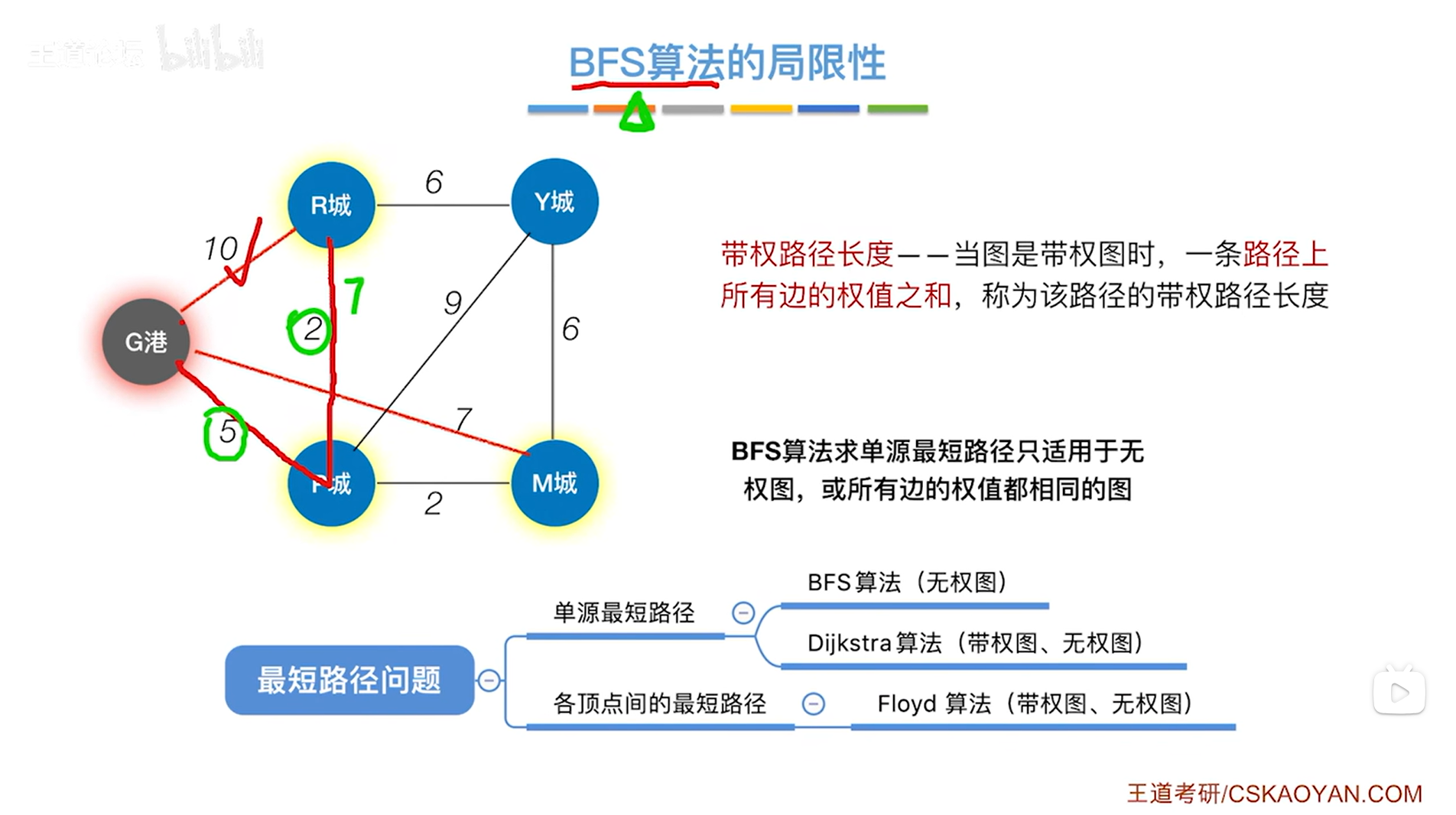
一.BFS算法的局限性：

如上图，BFS算法可以解决无权图的单源最短路径问题，

如果是解决带权图的单源最短路径问题，BFS算法就不适用了，如下图：

如上图，比如求G港到其他顶点的最短路径，

按照BFS算法，找到的G港到R城的最短路径就是从G港直接到R城的这条边即权值为10的边，因为G港的邻接顶点有一个R城，如下图：

如上图，实际上从G港到R城有一条更短的路径，就是G港->P城->R城，路径总长度只有7，

但如果按照BFS算法的话，R城就不会被第二次访问，也就不会得出G港->P城->R城这条更短的路径，如下图：

如上图，因此BFS算法不适用于带权图的单源最短路径问题，带权图的单源最短路径就需要用到Dijkstra算法，如下图：

---

二.回顾：带权路径长度->本章把带权路径长度简称为路径长度

---

三.Dijkstra算法：

1.前言：

以上述图片为例来解释Dijkstra算法，其中的图是有向图，

之所以不使用无向图，是因为无向图与有向图的原理一致，无向图的一条无向边就对应有向图的两条有向边，

因此解决了有向图的问题，无向图的问题也就迎刃而解了，如下图：

2.实例：

以上述图片的有向图为例，假设找出从顶点v0到达其他顶点的最短路径，如下图：

如上图，需要初始化三个数组final、dist、path（这3个数组中数据的内容都依次对应v0顶点、v1顶点、v2顶点、v3顶点、v4顶点）->

1.final数组表示目前为止是否找到从起点v0出发到达其他顶点的最短路径：

对于v0顶点，v0顶点对应的final值初始化为true，因为起点是v0，从起点v0到v0的最短路径就是0，意味着一开始就可以确定到达v0的最短路径，

对于v1、v2、v3、v4顶点，v1、v2、v3、v4对应的final值都初始化为false，因为一开始都无法确定从起点v0出发到达这些顶点的最短路径；

2.dist数组表示目前为止能够找到的最短路径的总长度：

对于v0顶点，起点v0到v0的最短路径长度为0，因此v0对应的dist数组的值为0，

对于v1顶点，一开始能找到一条v0直达v1的边，所以目前来看v0到v1的最短路径是10，因此v1对应的dist数组的值为10，

对于v4顶点，一开始能找到一条v0直达v4的边，所以目前来看v0到v4的最短路径是5，因此v4对应的dist数组的值为5，

对于v2和v3顶点，v2顶点和v3顶点并不存在从v0顶点直达的路径，所以把v2、v3对应的dist数组的值都初始化为无穷，表示目前还没有找到能够通往v2和v3的最短路径；

3.path数组用于记录每一个顶点在最短路径上的直接前驱：

对于v0顶点，v0顶点对于起点v0而言不存在最短路径，也就不存在直接前驱，所以v0对应的path值为-1，

对于v1顶点，目前能够确定的从起点v0到达v1的最短路径就是从v0直达v1，因此v1对应的path值初始化为0（0就是v0在path数组里的索引），

对于v4顶点，目前能够确定的从起点v0到达v4的最短路径就是从v0直达v4，因此v4对应的path值初始化为0，

对于v2和v3顶点，v0到达v2、v3顶点还没有相关的最短路径，因此也就没有直接前驱，所以v2、v3对应的path值都初始化为-1；

如下图：

如下图，开始第一轮的处理：

如上图，循环遍历三个数组final、dist、path全部的信息，从中找到还没确定最短路径的顶点即对应的final值为false、dist值最小的顶点，

显然在final值为false、dist值最小的顶点中找到的是v4顶点，开始处理v4顶点，

此时把v4顶点对应的final值设为true，表示现在已经可以确定对于v4顶点来说，从起点v0到v4的最短路径长度就是5，并且它的直接前驱是0索引上的顶点即v0，因此就确定了v0到v4的最短路径，

（这里之所以能确定从起点v0到v4的最短路径就是v0->v4且长度是5，是因为起点v0只指向v1和v4，如果不直接达到v4而是经过v1再到达v4，那么一定会经过v0到v1之间权值为10的边，10已经比v0直达v4之间的边的权值5大了，因此经过v1再到达v4显然不是最短路径，那么从v0直达v4就是最短路径）

如下图：

如上图，还需要继续检查v4指向的顶点即v1、v2、v3，最后只会修改对应的final值为false即目前还没有确定最短路径的顶点的dist和path信息，因此需要修改v1、v2、v3顶点对应的dist和path信息，

此时就需要检查到达v1、v2、v3，如果经过v4的话，那么有没有可能在之前找到的路径外存在更短的路径呢？

对于v1，在之前找到的路径中从v0到达v1的比较好的一条路径是长度为10，路径信息是v0->v1，但现在可以确定从起点v0到v4有一条长度为5的路径，而从v4到v1有一条长度为3的路径，因此如果v1顶点是v0->v4->v1过来的话，那么就可以找到一条总长度为5加3即8的路径，这条路径显然要比刚开始找到的长度为10的路径更好，所以要把v1对应的dist值修改为8，同时把v1对应的path值修改为4即前驱是v4（v4在path数组中的索引为4）；

对于v2，之前就没有找到能够从v0直达v2的路径，但是现在如果经过v4再到达v2的话，那么就可以找到一条总长度为5加9即14的路径，路径信息为v0->v4->v2，所以要把v2对应的dist值修改为14，同时把v2对应的path值修改为4即前驱是v4（v4在path数组中的索引为4）；

对于v3，之前就没有找到能够从v0直达v3的路径，但是现在如果经过v4再到达v3的话，那么就可以找到一条总长度为5加2即7的路径，路径信息为v0->v4->v3，所以要把v3对应的dist值修改为7，同时把v3对应的path值修改为4即前驱是v4（v4在path数组中的索引为4）；

如下图：

如下图，开始第二轮的处理：

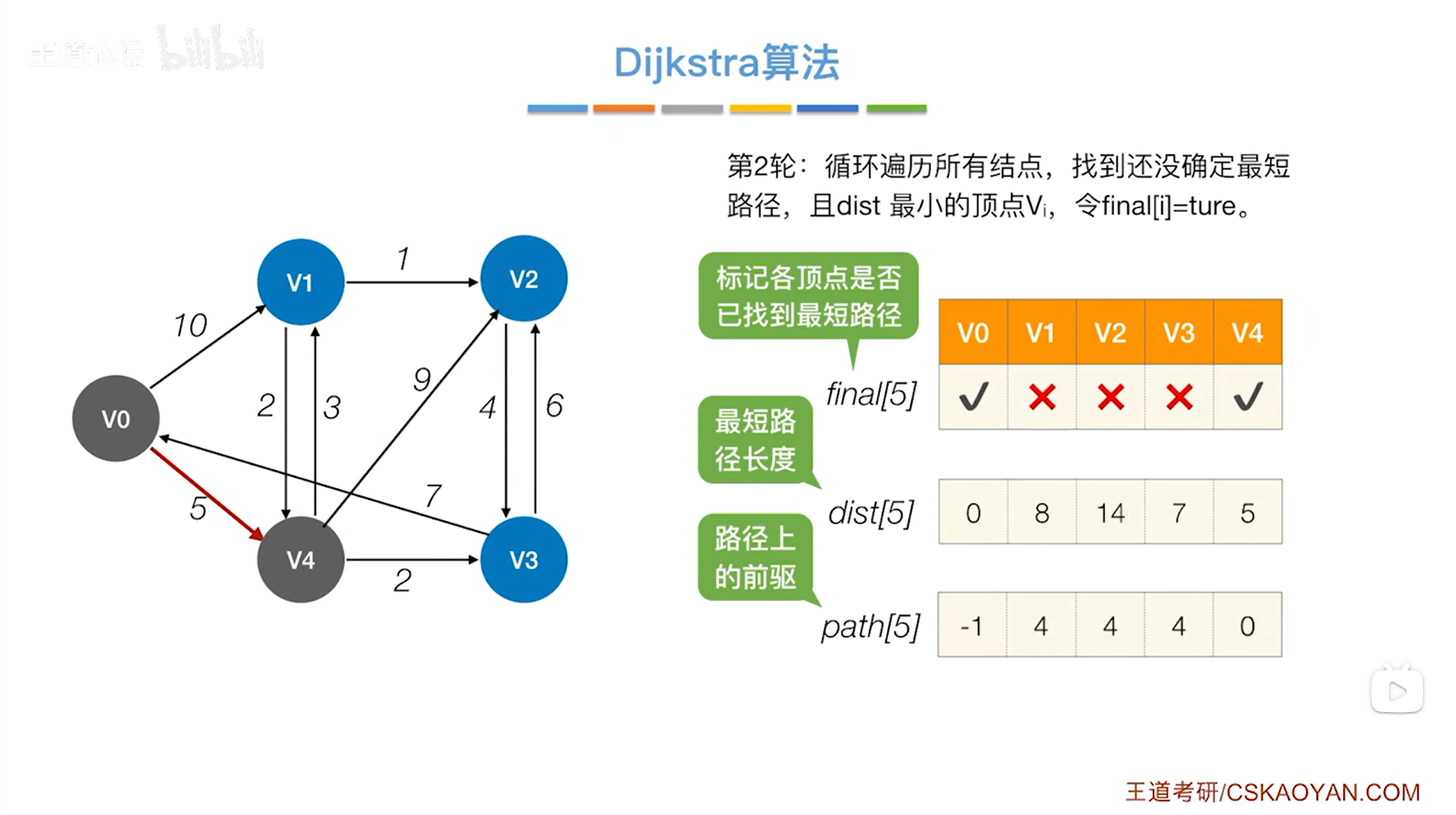
如上图，循环遍历三个数组final、dist、path全部的信息，从中找到还没确定最短路径的顶点即对应的final值为false、dist值最小的顶点，

显然在final值为false、dist值最小的顶点中找到的是v3顶点，开始处理v3顶点，

此时把v3顶点对应的final值设为true，表示现在已经可以确定对于v3顶点来说，从起点v0到v3的最短路径长度就是7，并且它的直接前驱是4索引上的顶点即v4，因此就确定了v0到v3的最短路径，

（这里之所以能确定从起点v0到v3的最短路径就是v0->v4->v3且长度是7，是因为直达v3的顶点只有v4和v2，从起点v0出发，到达v4的成本要比v2小，因此从v4到v3比从v2到v3更好，从起点v0到v4的最短路径是v0->v4，因此从起点v0到v3的最短路径为v0->v4->v3）

如下图：

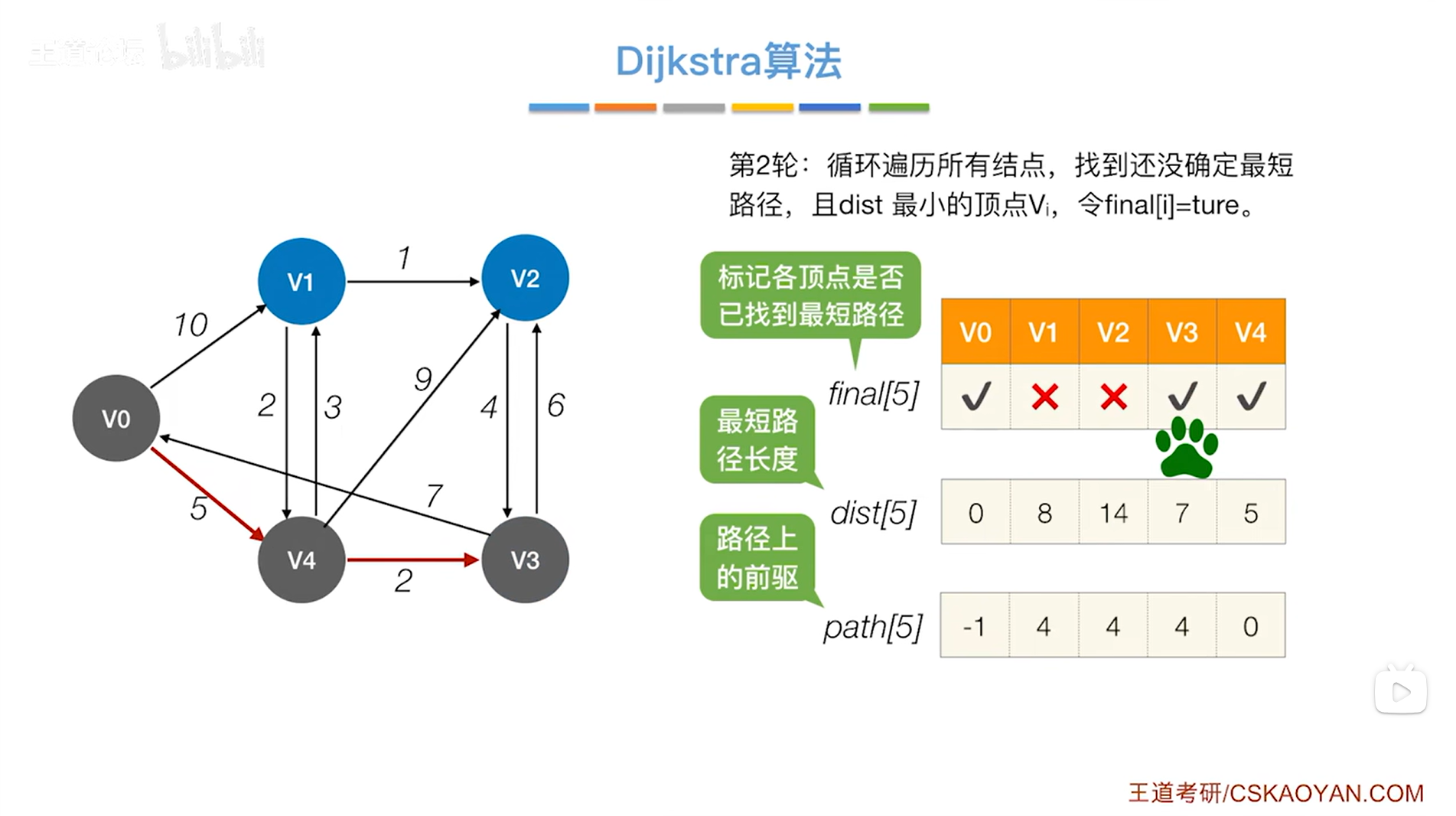
如上图，还需要继续检查v3指向的顶点即v0、v2，最后只会修改对应的final值为false即目前还没有确定最短路径的顶点的dist和path信息，因此需要修改v2顶点对应的dist和path信息，

此时就需要检查到达v2，如果经过v3的话，那么有没有可能在之前找到的路径外存在更短的路径呢？

对于v2，之前找到的从v0到达v2的最短路径长度为14，路径信息是v0->v4->v2，该路径最终是从v4直达v2的，但是现在如果从v3直达v2，那么就可以找到一条总长度为5加2加6即13的路径，路径信息是v0->v4->v3->v2，这个路径显然比v0->v4->v2更优秀（因为路径总长度更短），所以要把v2对应的dist值修改为13，同时把v2对应的path值修改为3即前驱是v3（v3在path数组中的索引为3）；

如下图：

如下图，开始第三轮的处理：

如上图，循环遍历三个数组final、dist、path全部的信息，从中找到还没确定最短路径的顶点即对应的final值为false、dist值最小的顶点，

显然在final值为false、dist值最小的顶点中找到的是v1顶点，开始处理v1顶点，

此时把v1顶点对应的final值设为true，表示现在已经可以确定对于v1顶点来说，从起点v0到v1的最短路径长度就是8，并且它的直接前驱是4索引上的顶点即v4，因此就确定了v0到v1的最短路径，

（这里之所以能确定从起点v0到v1的最短路径就是v0->v4->v1且长度是8，是因为直达v1的顶点只有v0和v4，v0->v1的成本要比v0->v4->v1高，所以v0->v4->v1是最优解）

如下图：

如上图，还需要继续检查v1指向的顶点即v2、v4，最后只会修改对应的final值为false即目前还没有确定最短路径的顶点的dist和path信息，因此需要修改v2顶点对应的dist和path信息，

此时就需要检查到达v2，如果经过v1的话，那么有没有可能在之前找到的路径外存在更短的路径呢？

对于v2，之前找到的从v0到达v2的最短路径长度为13，路径信息是v0->v4->v3->v2，该路径最终是从v3直达v2的，但是现在如果从v1直达v2，可以找到一条总长度为5加3加1即9的路径，路径信息为v0->v4->v1->v2，该路径要比v0->v4->v3->v2的成本更低，所以要把v2对应的dist值修改为9，同时把v2对应的path值修改为1即前驱是v1（v1在path数组中的索引为1）；

如下图：

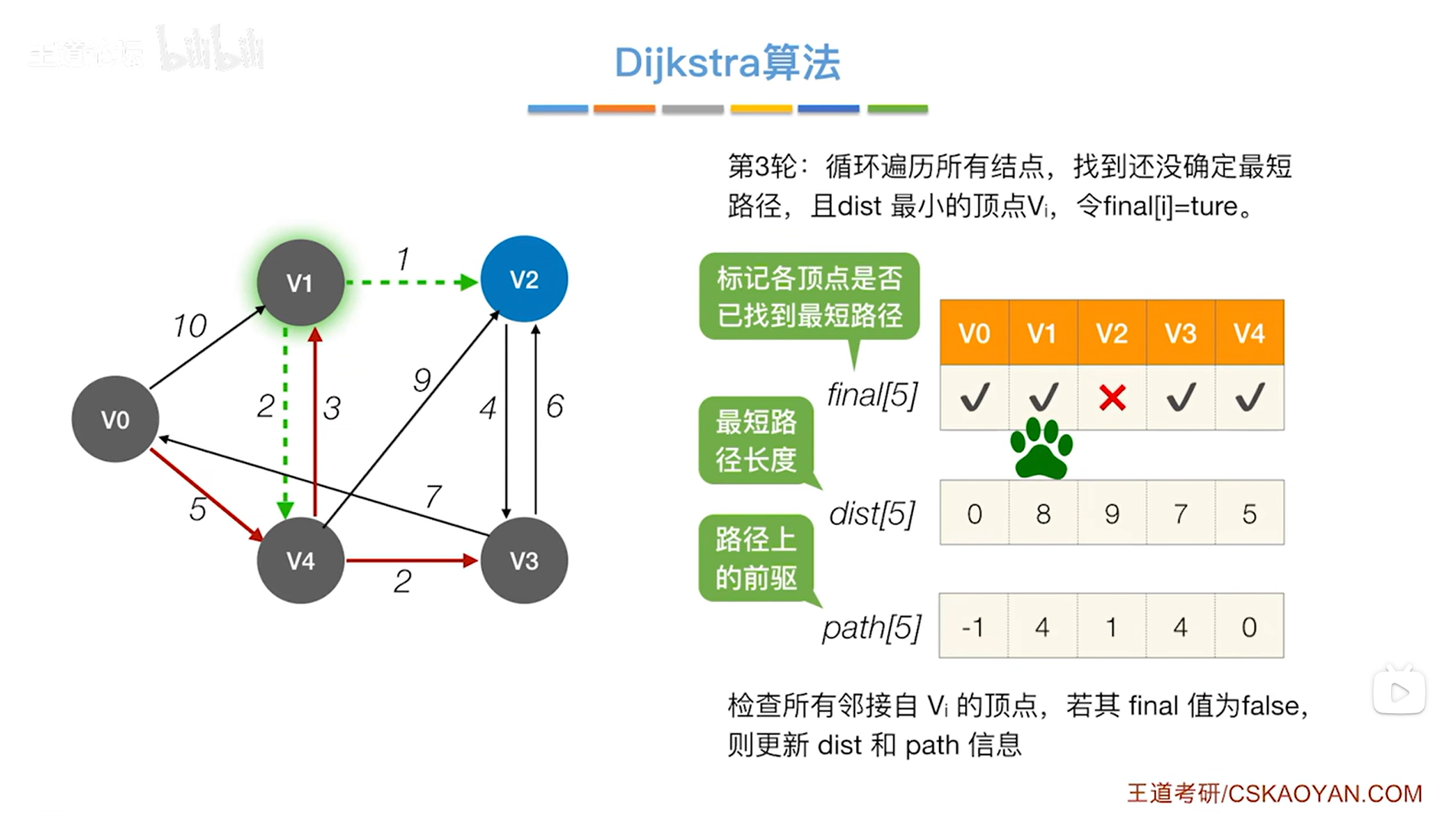
如下图，开始第四轮的处理：

如上图，循环遍历三个数组final、dist、path全部的信息，从中找到还没确定最短路径的顶点即对应的final值为false、dist值最小的顶点，

显然在final值为false、dist值最小的顶点中找到的是v2顶点，开始处理v2顶点，

此时把v2顶点对应的final值设为true，表示现在已经可以确定对于v2顶点来说，从起点v0到v2的最短路径长度就是9，并且它的直接前驱是1索引上的顶点即v1，因此就确定了v0到v2的最短路径，

如下图：

如上图，还需要继续检查v2指向的顶点即v3，最后只会修改对应的final值为false即目前还没有确定最短路径的顶点的dist和path信息，由于v3对应的final值为true，因此v3不会作任何处理，

至此v2处理完毕，如下图：

如上图，所有顶点对应的final值都为true即所有顶点都被处理完毕，

至此，Dijkstra算法结束。

3.对于本例如何使用数组信息？

对于最终得出的三个数组final、dist、path，

比如此时要找到起点v0到v2的最短路径的信息，

通过dist数组可知v0到v2的最短路径的总长度为9（就是dist[2]），

通过path数组可以得知该最短路径的内容，path数组中v2是从1索引上的顶点即v1过来的，v1是从4索引上的顶点即v4过来的，v4是从0索引上的顶点即v0过来的，此时找到了起点v0，因此可知该最短路径的内容为v0->v4->v1->v2。

4.时间复杂度：

假设图中的顶点的编号从0开始（第一个顶点记作v0，第二个顶点记作v1，以此类推），

现在要找到从v0到达其他顶点的最短路径，

初始化数组final、dist、path，

对于起点v0，

v0的final值设为true，因为一开始就可以确定从起点v0到v0的最短路径长度为0，意味着一开始就可以确定到达v0的最短路径，

v0的dist值为0，因为从起点v0到v0的最短路径长度为0，

v0的path值为-1，表示v0没有前驱顶点，因为v0本身就是起点，

对于其他顶点，

final值都设为false，因为一开始无法确定起点v0到达其他顶点的最短路径，

dist值都设为arcs[0] [k]，arcs[0] [k]表示的是从起点v0直达其他顶点的弧的长度，如果不存在弧（即无法直达）那么就设为无穷，

需要把起点v0指向的顶点的path值设为0（因为v0在path数组的0索引上，此时就代表前驱为v0），v0没有指向的顶点的path值设为-1（因为前驱不是v0）。

假设图中有n个顶点，接下来需要进行n-1轮处理，因为每一轮的处理都能够确定一个新顶点的最短路径，所以在刚开始只有n-1个顶点没有确定最短路径的情况下，由于每一轮可以确定一个，所以需要n-1轮处理，

在每一轮的处理当中都需要循环遍历所有的顶点找到一个final值为false、dist值最小的顶点，也就是说每一轮的处理都需要把final、dist数组扫描一遍，这些数组的总长度都为n（和顶点个数一样），也就是从final、dist数组中找出final值为false、dist值最小的顶点需要O(n)的时间复杂度（遍历final数组和dist数组是先后关系，不是同时进行的），

除了找到final值为false、dist值最小的顶点之外，还需要检查这一轮中选中的顶点它所指向的顶点，

如果图采用邻接矩阵存储，要找到某一个顶点指向的所有顶点，就需要扫描和这个顶点相关的那一整行（这是有向图，邻接矩阵不对称，就不能扫描列了），扫描邻接矩阵的一整行需要O(n)的时间复杂度即每一轮循环要遍历2n个顶点，所以每一轮的处理总共需要O(2n)的时间复杂度，等价于O(n)，

如果图采用邻接表存储，那么找到某一个顶点指向的所有顶点就不需要O(n)的时间复杂度了，因为邻接表中某一个顶点对应的链表已经把该顶点指向的所有顶点的信息都列出来了，不需要遍历所有顶点来找指向的顶点了，但由于从final、dist数组中找出final值为false、dist值最小的顶点无论怎样都需要扫描一遍数组，所以总的时间复杂度为O(n)，

由于需要n-1轮处理，所以整个算法的时间复杂度就是O( n * (n-1) )，等于O( n * n - n )，等价于O( n * n )，

若图中有V个顶点，总的时间复杂度就是O( |V| * |V| )。

---

四.Dijkstra算法 V.S. Prim算法的实现思想：

Dijkstra算法，如下图：

Prim算法，如下图：

对于Prim算法，lowCost数组记录的是图中顶点加入到目前组建的生成树里的最小代价，

而Dijkstra算法，dist数组记录的是当前顶点到达某一个指定顶点的最短路径的值，

但实际上Dijkstra算法里的dist数组和Prim算法里的lowCost数组作用类似，

假设图中有V个顶点，由于Prim算法和Dijkstra算法的执行过程类似，所以Prim算法和Dijkstra算法的时间复杂度也是相同的，都是O( |V| * |V| )。

---

五.Dijkstra算法不适用于负权值带权图：

如果带权图里存在权值为负数的边，那么Dijkstra算法就有可能会失效，找不到最短的带权路径，

如下图的例子，假设找出从顶点v0到达其他顶点的最短路径，

需要初始化三个数组final、dist、path（这3个数组中数据的内容都依次对应v0顶点、v1顶点、v2顶点）->

1.final数组表示目前为止是否找到从起点v0出发到达其他顶点的最短路径：

对于v0顶点，v0顶点对应的final值初始化为true，因为起点是v0，从起点v0到v0的最短路径就是0，意味着一开始就可以确定到达v0的最短路径，

对于v1、v2顶点，v1、v2对应的final值都初始化为false，因为一开始都无法确定从起点v0出发到达这些顶点的最短路径；

2.dist数组表示目前为止能够找到的最短路径的总长度：

对于v0顶点，起点v0到v0的最短路径长度为0，因此v0对应的dist数组的值为0，

对于v1顶点，一开始能找到一条v0直达v1的边，所以目前来看v0到v1的最短路径是10，因此v1对应的dist数组的值为10，

对于v2顶点，一开始能找到一条v0直达v2的边，所以目前来看v0到v2的最短路径是7，因此v2对应的dist数组的值为7，

3.path数组用于记录每一个顶点在最短路径上的直接前驱：

对于v0顶点，v0顶点对于起点v0而言不存在最短路径，也就不存在直接前驱，所以v0对应的path值为-1，

对于v1顶点，目前能够确定的从起点v0到达v1的最短路径就是从v0直达v1，因此v1对应的path值初始化为0（0就是v0在path数组里的索引），

对于v2顶点，目前能够确定的从起点v0到达v2的最短路径就是从v0直达v2，因此v2对应的path值初始化为0，

如下图：

如上图，开始第一轮的处理：

循环遍历三个数组final、dist、path全部的信息，从中找到还没确定最短路径的顶点即对应的final值为false、dist值最小的顶点，

显然在final值为false、dist值最小的顶点中找到的是v2顶点，开始处理v2顶点，

此时把v2顶点对应的final值设为true，表示现在已经可以确定对于v2顶点来说，从起点v0到v2的最短路径长度就是7，并且它的直接前驱是0索引上的顶点即v0，因此就确定了v0到v2的最短路径，

如下图：

如上图，开始第二轮的处理：

循环遍历三个数组final、dist、path全部的信息，从中找到还没确定最短路径的顶点即对应的final值为false、dist值最小的顶点，

显然在final值为false、dist值最小的顶点中找到的是v1顶点，开始处理v1顶点，

此时把v1顶点对应的final值设为true，表示现在已经可以确定对于v1顶点来说，从起点v0到v1的最短路径长度就是10，并且它的直接前驱是0索引上的顶点即v0，因此就确定了v0到v1的最短路径，

如下图：

如上图，所有顶点对应的final值都为true即所有顶点都被处理完毕，

至此，Dijkstra算法结束。

但事实上，如果是从v0->v1->v2这条路径到达v2，由于v1与v2之间的边的权值是负数，所以该条带权路径长度总和为10加-5即5，显然比Dijkstra算法找到的最短路径长度为7的路径v0->v2成本更低，

因此对于v2，使用Dijkstra算法找到的最短路径并不是最优的，

所以Dijkstra算法不适合有负权值边的带权图。

（图什么时候会用到带负权值的边呢？

例一：比如吃鸡游戏，会有一个毒圈，比如此时站在毒圈内，就会一直掉血，以上图为例，假设站在毒圈内v0的位置，现在可以选择直接跑到毒圈外v2的位置，整个跑毒的过程会掉7点血，第二个方案是毒圈内v1这个地方有一个血包，可以先到v1处捡到血包，再跑出毒圈，到达v1会掉10滴血，再捡血包，跑出毒圈之后通过血包可以恢复5点血，总体来看用第二个方案来跑毒的话掉血的代价更小，所以这种场景下就会用到带负权值的边的图。

例二：以上图为例，此时有v0、v1、v2三个地方，可以选择从v0直接开车到v2，开的是电动车，要消耗7格电，还有一种方案可以先从v0开到v1，需要消耗10格电，但是从v1到v2这一段路由于都是下坡，因此可以不费电的让车滑下去，车在往下滑的过程中又可以利用轮子的转动来自己发电，那整个下滑的过程中又可以恢复5格电，所以用第二种方案来走到v2，总的耗电量更低）。

---