VSLAM系列原创04讲 | 四叉树实现ORB特征点均匀化分布：原理+代码

本文系ORB-SLAM2原理+代码实战系列原创文章，对应的视频课程见：

如何真正搞透视觉SLAM？

大家好，从今天开始我们陆续更新ORB-SLAM2/3系列的原创文章，以小白和师兄对话的形式阐述背景原理+代码解析，喜欢的点个赞分享，支持的人越多，更新越有动力！如有错误欢迎留言指正！

代码注释地址：

https://github.com/electech6/ORB_SLAM2_detailed_comments

VSLAM系列原创01讲 | 深入理解ORB关键点提取：原理+代码

VSLAM系列原创02讲 | ORB描述子如何实现旋转不变性？原理+代码

VSLAM系列原创03讲 | 为什么需要ORB特征点均匀化？

接上回继续。。。

四叉树实现特征点均匀化分布

师兄：四叉树实现特征均匀化分布的方法是重点，也是一个难点，我先讲一下步骤和原理：

第1步：首先确定初始的节点（node）数目。根据图像宽高比取整来确定，所以一般的VGA () 分辨率图像刚开始的时候只有一个节点，也是四叉树的根节点。

下面我们用一个具体的例子来分析四叉树是如何帮助我们均匀化选取特定数目的特征点的。假设初始节点只有1个，那么所有的特征点都属于该节点。我们目标是均匀的选取 25 个特征点，那么后面我们就需要分裂出25个节点，然后从每个节点中选取一个代表性的特征点。

第2步：节点第1次分裂，1个根节点分裂为4个节点。如下图所示，分裂之后根据图像的尺寸划分节点的区域，对应的边界为 ，分别对应左上角、右上角、左下角、右下角的四个坐标。有些坐标会被多个节点共享，比如图像中心点坐标就同时被  四个点共享。落在某个节点区域范围内的所有特征点都属于该节点的元素。

然后统计每个节点里包含特征点的数目，如果某个节点里特征点数目为 0，则删掉该节点，如果某个节点里特征点数目为 1，则该节点不再进行分裂。判断此时的节点总数是否超过设定值 25，如果没有超过则继续对每个节点分裂。

 

这里需要注意的是一个母节点分裂为 4 个子节点后，需要在节点链表里删掉原来的母节点，所以实际上一次分裂净增加了 3 个节点。所以下次分裂后节点的总数我们是可以提前预估的，计算方式为：（当前节点总数 + 即将分裂的节点总数  3 ），对于图示来说，下次分裂最多可以得到  个节点，显然还是没有达到 25 的要求，需要继续分裂。

第3步：对上一步得到的 4 个节点分别进行一分为四的操作，然后统计分裂后的每个节点里包含特征点的数目，我们可以看到已经有 2 个节点里的特征点数目为 0，于是在节点链表里删掉这 2 个节点（下图中标记为 ）。如果某个节点里特征点数目为 1，则该节点不再进行分裂。此次分裂总共得到 14 个节点。

 

第4步：上一步得到的 14 个节点继续进行一分四的操作。预计这次分裂最多可以得到  个节点，已经超过我们需要提取 25 个特征点数目的需求。此时需要注意了，我们不需要把所有的节点都进行分裂，我们只需要在分裂得到的所有节点数目刚刚达到 25 时，即可停止分裂，这样操作的目的一方面是可以避免多分裂后再删除而做无用功，另一方面，因为是指数级分裂，所以也大大加速了四叉树分裂的过程。

那么，如何选取分裂的顺序呢？源码里采用的策略是对所有节点按照内部包含的特征点数目进行排列，优先分裂特征点数目多的节点，这样做的目的是使得特征密集的区域能够更加细分。对于包含特征点较少的节点，有可能因为提前达到要求而不再分裂。下图中绿色方框内的节点就是因为包含的特征点数目太少（这里包括只有 1 个也不再分裂的情况），分裂的优先级很低，最终在达到要求的节点数目前没有再分裂。

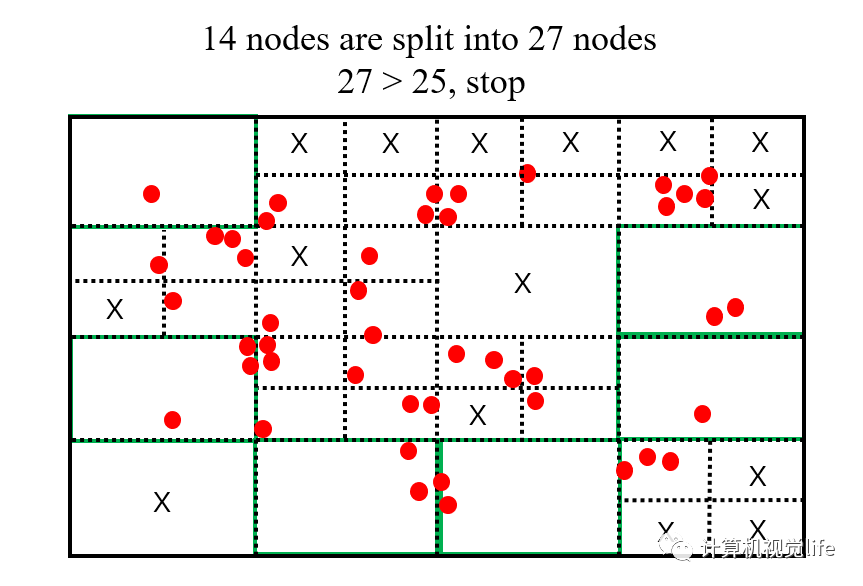
第5步：上一步中我们已经得到了所需要的 25 个节点，只需要从每个节点中选出角点响应值最高的特征点，作为该节点的唯一特征点，该节点内其他低响应值的特征点全部删掉。这样我们就得到了均匀化后的、需要数目的特征点。

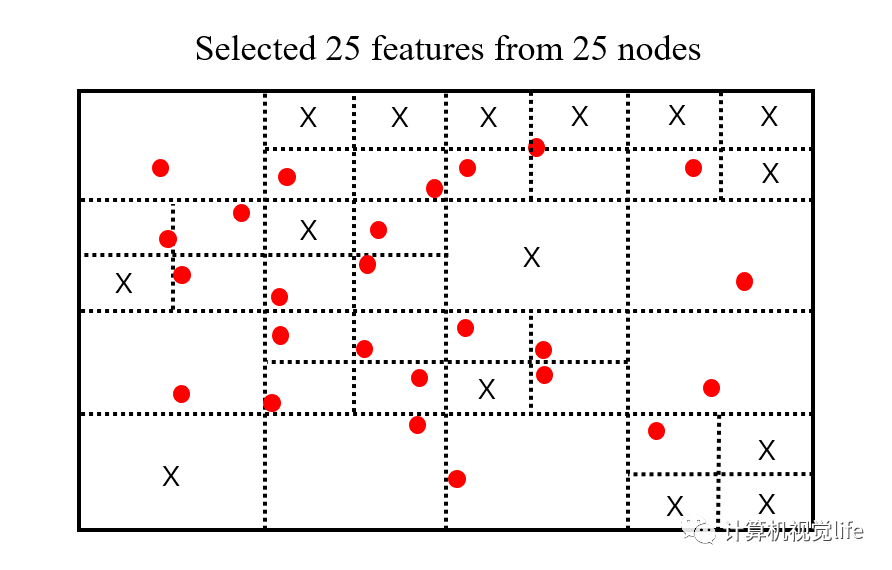
以上就是使用四叉树对图像特征点进行均匀化的原理，详细注释代码见：

/**
 * @brief 使用四叉树法对一个图像金字塔图层中的特征点进行平均和分发
 * 
 * @param[in] vToDistributeKeys     等待进行分配到四叉树中的特征点
 * @param[in] minX                  当前图层的图像的边界
 * @param[in] maxX 
 * @param[in] minY 
 * @param[in] maxY 
 * @param[in] N                     希望提取出的特征点个数
 * @param[in] level                 指定的金字塔图层
 * @return vector<cv::KeyPoint>     已经均匀分散好的特征点容器
 */
vector<cv::KeyPoint> ORBextractor::DistributeOctTree(const vector<cv::KeyPoint>& vToDistributeKeys, const int &minX,
                                       const int &maxX, const int &minY, const int &maxY, const int &N, const int &level)
{
    // Step 1 根据宽高比确定初始节点数目
 //计算应该生成的初始节点个数，根节点的数量nIni是根据边界的宽高比值确定的，一般是1或者2
    // ! bug: 如果宽高比小于0.5，nIni=0, 后面hx会报错
    const int nIni = round(static_cast<float>(maxX-minX)/(maxY-minY));

 //一个初始的节点的x方向有多少个像素
    const float hX = static_cast<float>(maxX-minX)/nIni;

 //存储有提取器节点的链表
    list<ExtractorNode> lNodes;

 //存储初始提取器节点指针的vector
    vector<ExtractorNode*> vpIniNodes;

 //重新设置其大小
    vpIniNodes.resize(nIni);

 // Step 2 生成初始提取器节点
    for(int i=0; i<nIni; i++)
    {      
  //生成一个提取器节点
        ExtractorNode ni;

  //设置提取器节点的图像边界
        ni.UL = cv::Point2i(hX*static_cast<float>(i),0);    //UpLeft
        ni.UR = cv::Point2i(hX*static_cast<float>(i+1),0);  //UpRight
  ni.BL = cv::Point2i(ni.UL.x,maxY-minY);          //BottomLeft
        ni.BR = cv::Point2i(ni.UR.x,maxY-minY);       &nb