正反馈增强CMOS放大器增益

亚100纳米多千兆赫CMOS放大器设计中用于增益增强的正反馈

1. 引言

低于100nm的MOS器件沟道长度缩放已开始对模拟集成电路设计领域带来重大问题。数字电路通常从缩放中受益，因为器件速度更快且功耗更低。近年来，片上系统（SOC）设计趋势推动了数字和模拟子系统共存于同一单片基板上，使得许多模拟设计进入这些缩放工艺。通常，这些SOC中的模拟电路采用高电压输入/输出器件来实现所需的电路性能。这增加了成本，并因引入多电压域及其接口而使设计更加复杂。理想情况下，模拟电路应使用与数字设计相同的低压器件进行设计。然而，缩放的影响已导致这些器件的低压模拟性能下降。

一个例子是最大本征增益（MIG）的降低。MIG 是单个晶体管 [1–3] 的小信号跨导 gm 与小信号输出阻抗 ro 的乘积。广义缩放理论 [4] 无法预测这种 MIG 的退化，也无法预测在亚100纳米技术中设计的模拟电路所观察到的 MIG 退化的影响。此外，按比例缩小的器件通常针对数字性能进行优化，这意味着在 CMOS 技术缩放过程中，MIG 并不是晶圆厂考虑因素中的关键指标。

从模拟设计师的角度来看，对于缩放限制几乎无能为力，因此电路解决方案是补偿 MIG退化的唯一可行选择。本文提出利用正反馈作为解决本征增益退化问题的一种方案。正反馈此前已在其他文献中讨论过[6–8]。本研究是对该方法的扩展，通过测量正反馈对CMOS放大器频率响应的影响，扩展了我们之前的工作[5]。正反馈以通用方式进行了分析，因此只要增加一个小的反馈因子，便可应用于任何满足所述条件的电路拓扑。该方法不要求电路必须包含在负反馈环路中以保持稳定性。

本工作提出了一种用于推导采用正反馈放大器基本行为的模型。基于该模型推导出的理论被应用于标准差分放大器级，并通过制造的硅实验数据进行了验证。

2. 改进型放大器模型

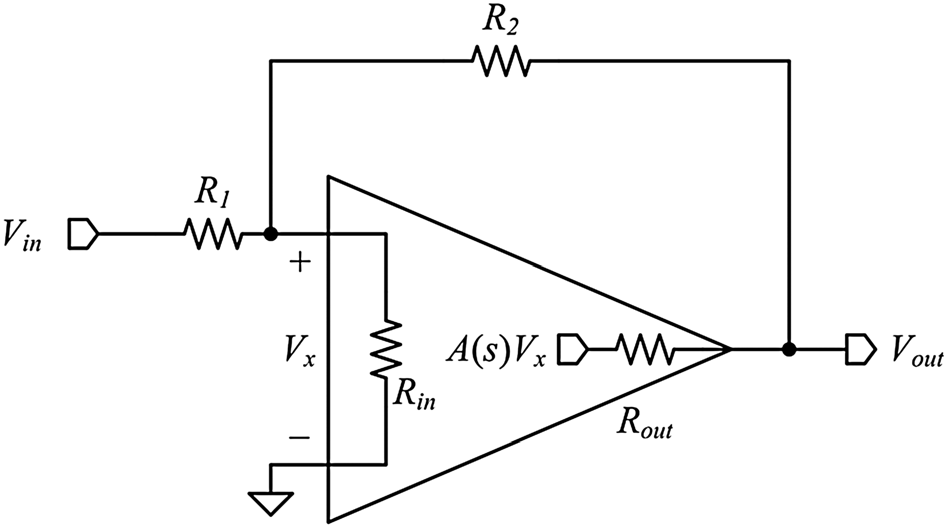
图1所示的放大器包含有限的输入和输出阻抗。该模型的输出是输入端子处的电压Vx乘以放大器增益传递函数A(s)，并通过电阻Rout实现。由于Rin、Rout和A(s)是基准放大器的函数，R1和R2则是用于优化放大器性能的设计参数。

对该模型的节点分析表明，得到的传递函数为

$$
H \left( s \right) = \frac{G_1 G_2 + A \left( s \right) G_{out}}{G_2 + G_{out}} \cdot \frac{1}{1 - \frac{G_2}{G_1 + G_2 + G_{in}} \cdot \frac{G_2 + A \left( s \right) G_{out}}{G_2 + G_{out}}}
\tag{1}
$$

其中Gin、Gout、G1和G2分别是Rin、Rout、R1和R2的电导。在传统反馈形式中，(1)式可写为

$$
H \left( s \right) = \frac{A_{OL} \left( s \right)}{1 - A_{OL} \left( s \right) b_{OL}}
\tag{2}
$$

其中

$$
A_{OL} \left( s \right) = \frac{G_1}{G_1 + G_2 + G_{in}} \cdot \frac{G_2 + A \left( s \right) G_{out}}{G_2 + G_{out}}
\tag{3}
$$

and

$$
b_{OL} = \frac{G_2}{G_1}
\tag{4}
$$

将A(s)的单极点模型代入(1)，其直流增益为A_DC，−3dB带宽为p1，可得H(s)

$$
H \left( s \right) = \frac{\frac{G_1 G_2}{(G_1 + G_2 + G_{in})(G_2 + G_{out}) - G_2^2}}{s + p_1 \left(1 + \frac{A_{DC} G_{out}}{G_2}\right)} \cdot \frac{1}{s + p_1 \left[\frac{(G_1 + G_2 + G_{in})(G_2 + G_{out}) - G_2^2 - A_{DC} G_2 G_{out}}{(G_1 + G_2 + G_{in})(G_2 + G_{out}) - G_2^2}\right]}
\tag{5}
$$

具有直流增益

$$
H_{DC} = \frac{G_1 (G_2 + A_{DC} G_{out})}{(G_1 + G_2 + G_{in})(G_2 + G_{out}) - G_2^2 - A_{DC} G_2 G_{out}} \equiv \frac{\Phi}{\Psi};
\tag{6}
$$

和 −3dB带宽的

$$
p_{1H} = p_1 \cdot \frac{\Psi}{\Psi + A_{DC} G_2 G_{out}};
\tag{7}
$$

其中 Φ 和 Ψ 为了方便起见，分别定义为 (6) 的分子和分母。

这里的分析涉及寻找一组R2值，这些值能够提高增益但不会产生右半平面（RHP）极点。产生RHP极点的R2边界值，同时也是导致分母为零、使闭环增益趋近于无穷大的R2值。满足这些条件的解得出了以下有效的R2范围

$$
R_2 > -\frac{(G_1 + G_{in} + G_{out})(1 - A_{DC})}{G_{out}(G_1 + G_{in})};
\tag{8}
$$

$$
R_2 < \frac{G_1 (1 - A_{DC}) - G_{in} A_{DC} - G_{out} (1 - A_{DC}) A_{DC}}{A_{DC} G_{in} G_{out}};
\tag{9}
$$

方程(8)和(9)给出了基于稳定性和增益提升的反馈电阻有效范围。然而，方程(8)表明可能存在一个最小所需增益，以确保R2范围的下限为正值。在此条件下，开环增益必须至少达到

$$
A_{DC} > 1 + \frac{G_1 + G_{in}}{G_{out}} \approx 1 + \frac{R_{out}}{R_1};
\tag{10}
$$

(10) 中的近似基于输入阻抗远大于 R1 和 Rout ——这对于基于MOSFET的输入级来说是合理的预期。可以对 A_DC 施加一个附加约束，使得 (5) 不具有右半平面极点

$$
A_{DC} < 1 + \frac{(R_2 + R_{out}) \cdot (G_1 + G_{in})}{1} \approx \frac{R_2 + R_{out}}{R_1};
\tag{11}
$$

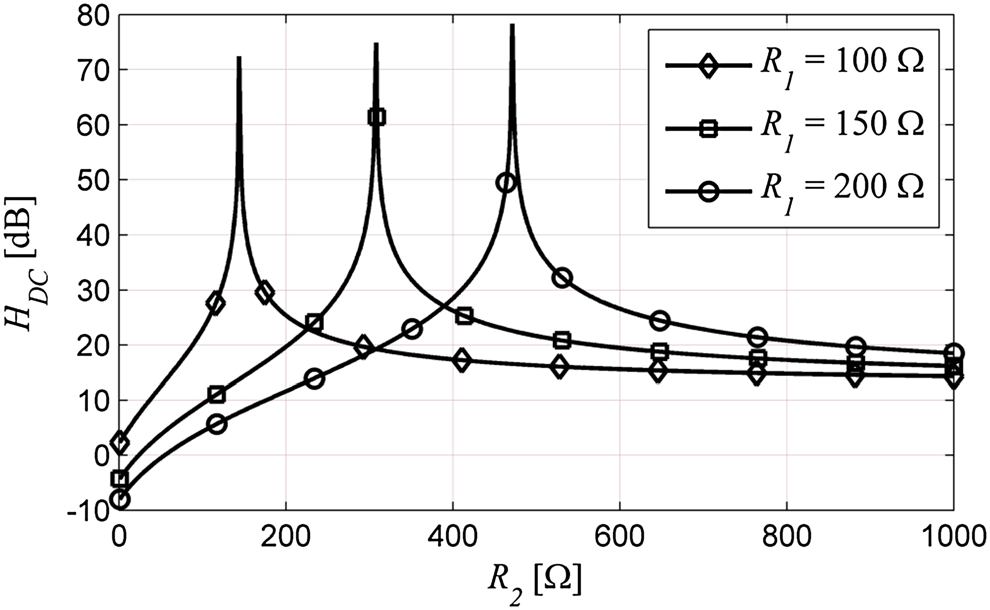
方程(8)和(9)有助于在给定开环增益或反馈因子的情况下，为设计者对R2的取值设定限制。方程(10)和(11)有助于定义开环放大器设计的限制。这四个方程的结合使得该通用架构能够实现正反馈回路。图2显示了H_DC 随R2 和R1 变化的幅度。在H_DC 趋近于无穷大的点（由方程(8)描述的边界）左侧，系统变得不稳定。

3. 正反馈的扩展分析

以这种方式在放大器中应用正反馈会增加增益，但代价是带宽减小。设计人员通常还需要考虑其他电路参数要求，本节将在本文定义的模型背景下探讨其中一些因素。以下分析重点对比了常用的负反馈与所提出的正反馈之间的差异。

3.1. 增益带宽积

对正反馈结构的理想分析表明，施加反馈后增益带宽积（GBP）保持不变。然而，当存在非理想阻抗时，这一结论不再成立。两者之间的关系可以表示为

$$
GBPr = \frac{GBP_{CL}}{GBPO_L} = \frac{\Phi}{A_{DC} \cdot [\Psi + A_{DC} G_2 G_{out}]};
\tag{12}
$$

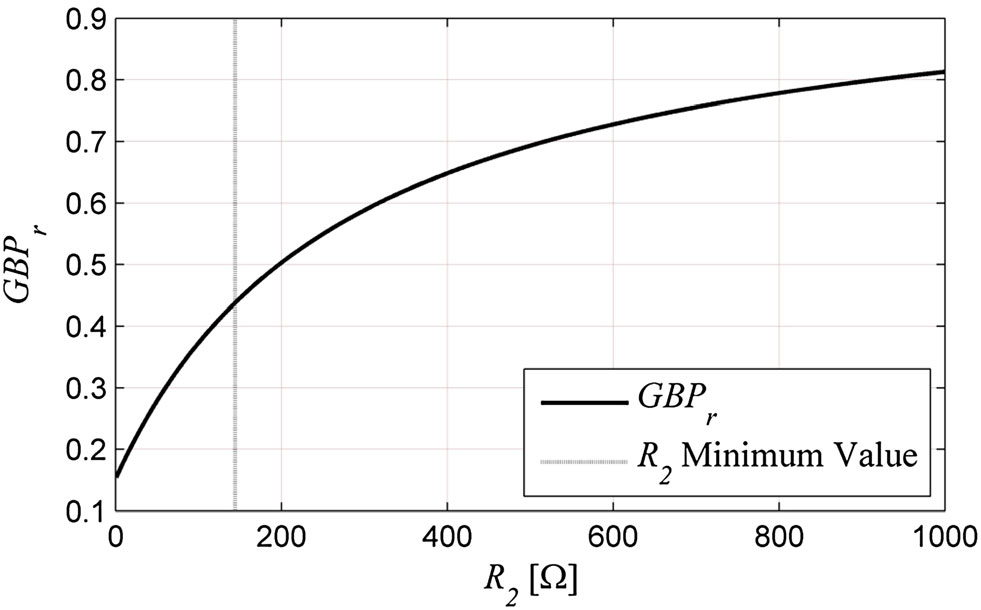
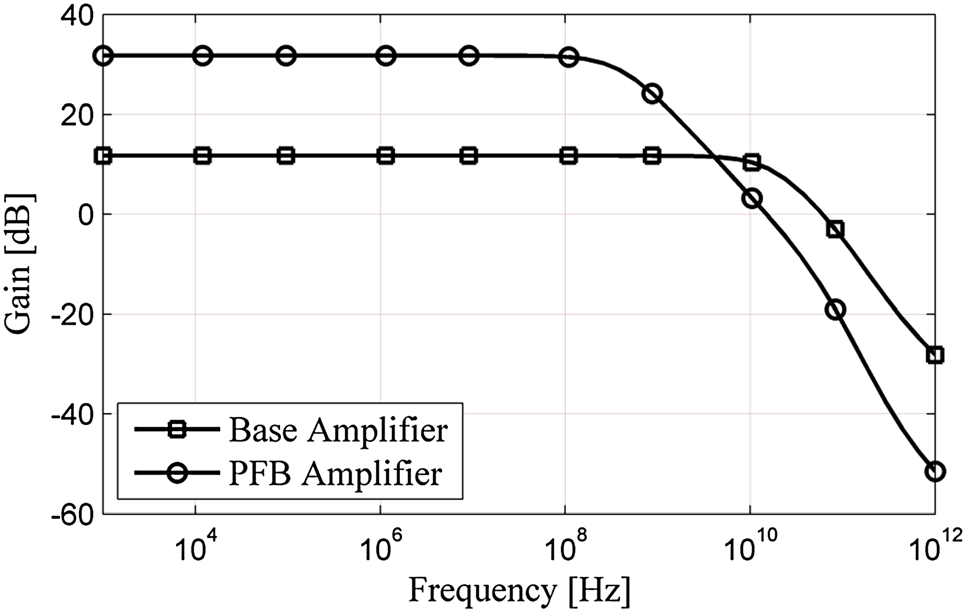
其中，GBPr为增益带宽积比率，GBPCL为闭环放大器的增益带宽积，GBPOL为开环放大器的增益带宽积。理想情况下，该比值应为1。然而，图3显示，随着R2的增大，GBPr也随之增加。这与增益分析结果相反，因为较小的R2能带来更大的闭环增益提升。这种增益带宽积退化在图4的交流仿真图中也清晰可见，其中正反馈情况下的单位增益频率（约等于增益带宽积）有所降低。

3.2. 输入和输出阻抗

与负反馈类似，施加正反馈会导致放大器的输入阻抗发生变化。这种变化可以被描述为

$$
Z_{in} \left( s \right) = \left[ G_1 \left( 1 - \frac{G_1 (G_2 + G_{out})}{(G_1 + G_2 + G_{in})(G_2 + G_{out}) - G_2 (G_2 + A \left( s \right) G_{out})} \right) \right]^{-1};
\tag{13}
$$

遵循前一节提出的稳定性条件的设计会导致放大器的输入阻抗降低。有趣的是，在特定的增益和阻抗条件下，该参数可能变为负值。这在设计过程中应予以充分考虑。

闭环放大器的输出阻抗也因应用正反馈而发生变化。放大器的最终输出阻抗可以表示为

$$
Z_{out} \left( s \right) = \frac{G_1 + G_2 + G_{in}}{(G_1 + G_2 + G_{in})(G_2 + G_{out}) - G_2 (G_2 + A \left( s \right) G_{out})};
\tag{14}
$$

应用本文的稳定性条件，正反馈有助于提高放大器的输出阻抗。这些结果与负反馈的情况相反。

3.3. 输入参考失调

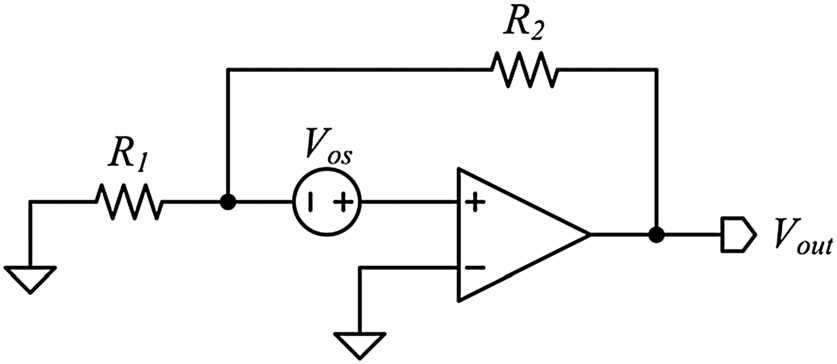
正反馈还会影响基本放大器的输入参考偏移。为了便于说明，忽略输入和输出阻抗，图5显示了一个具有输入参考偏移Vos的正反馈放大器。该结构的闭环增益可以表示为

$$
A_v = \frac{V_{out}}{V_{in}} = \frac{A_f}{1 - A_f b_f}
\tag{15}
$$

其中

$$
A_f = A_{DC} \cdot \frac{R_2}{R_1 + R_2}
\tag{16}
$$

and

$$
b_f = \frac{R_1}{R_2}
\tag{17}
$$

偏移增益可以计算为

$$
A_{os} = \frac{V_{out}}{V_{os}} = \frac{A_{DC}}{1 - A_{DC} \cdot \frac{R_1}{R_1 + R_2}} = \frac{A_f (1 + b_f)}{1 - A_f b_f}
\tag{18}
$$

产生一个输入参考偏移

$$
V_{os,in} = \frac{A_{os}}{A_v} \cdot V_{os} = (1 + b_f) \cdot V_{os}
\tag{19}
$$

与负反馈的情况类似，正反馈中的bf大于零，因此放大器的失调比开环放大器略有增加。

虽然这一效应与负反馈相似，但在将正反馈嵌入更大的负反馈环路中时，应考虑失调的增加。这一点在[8]中未被考虑。

3.4. 输入参考噪声

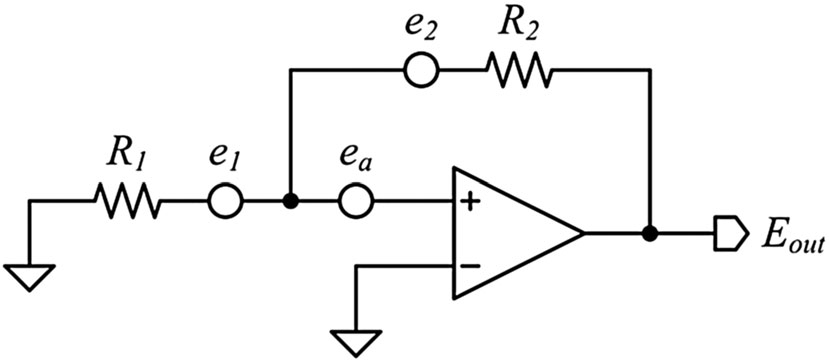
通过评估图6中的结构，可以对正反馈放大器进行输入参考噪声分析，其中ea为基准放大器输入参考噪声，e1和e2分别为反馈电阻R1和R2产生的热噪声。该结构的总输出均方根噪声为

$$
E^2_{out} = e^2_a \left[ \frac{A_f (1 + b_f)}{1 - A_f b_f} \right]^2 + e^2_1 \left[ \frac{A_f}{1 - A_f b_f} \right]^2 + e^2_2 \left[ \frac{A_f b_f}{1 - A_f b_f} \right]^2
\tag{20}
$$

因此，输入参考噪声是

$$
E^2_{in} = e^2_a (1 + b_f)^2 + \frac{4kT\Delta f}{R_1} (1 + b_f)
\tag{21}
$$

与输入参考偏移的情况类似，基准放大器输入参考噪声被bf所增加。由于电阻热噪声引起的噪声贡献既取决于bf，也取决于R1的绝对值。同样地，对于输入参考偏移而言，对类似负反馈结构的分析得出完全相同的行为。尽管bf、R1和R2的值会有显著差异，但正反馈相对于传统反馈设计并不会以一种根本不同的方式劣化噪声性能。

3.5. 共模抑制比

最后，正反馈会改变基本放大器的共模抑制比（CMRR），即CMRROL。典型的CMRR分析将共模增益Ac定义为差分增益Ad由于差分对尾电流源阻抗的源极退化而被某个因子降低后的结果。因此，共模增益可以定义为

$$
A_c = \frac{A_d}{CMRROL}
\tag{22}
$$

将源极退化概念应用于正反馈放大器，可以计算共模增益

$$
A_c = \frac{A_f / CMRROL}{1 - A_f b_f / CMRROL}
\tag{23}
$$

因此CMRR为

$$
CMRR = \frac{A_d}{A_c} = \frac{A_f (1 - A_f b_f)}{1 - A_f b_f / CMRROL} \cdot \frac{CMRROL}{A_f} = CMRROL - \frac{A_f b_f}{1 - A_f b_f}
\tag{24}
$$

由于正反馈设计方法要求Af bf必须介于零和一之间，(24)式表明正反馈放大器的 CMRR实际上得到提高，因而性能更优。

该结果与负反馈CMRR进行比较

$$
CMRR_{NFB} = \frac{CMRROL + A_f b_f}{1 + A_f b_f}
\tag{25}
$$

在这种情况下，负反馈设计要求Af bf >> 1，因此

$$
CMRR_{NFB} \approx \frac{CMRROL}{A_f b_f} + 1
\tag{26}
$$

这意味着负反馈实际上会降低CMRR。

3.6. 灵敏度分析

随着工艺尺寸缩小，MIG的性能逐渐退化，利用正反馈作为一种稳定的技术来以带宽为代价提升直流增益的能力变得更加可行。开环增益退化——作为MIG退化导致反馈因子b的范围增大且更具实用性。正反馈元件可以选择为能够实现直流增益的极大提升；然而，这种增益的提升是以对正反馈元件和开环放大器参数变化的敏感性为代价的。

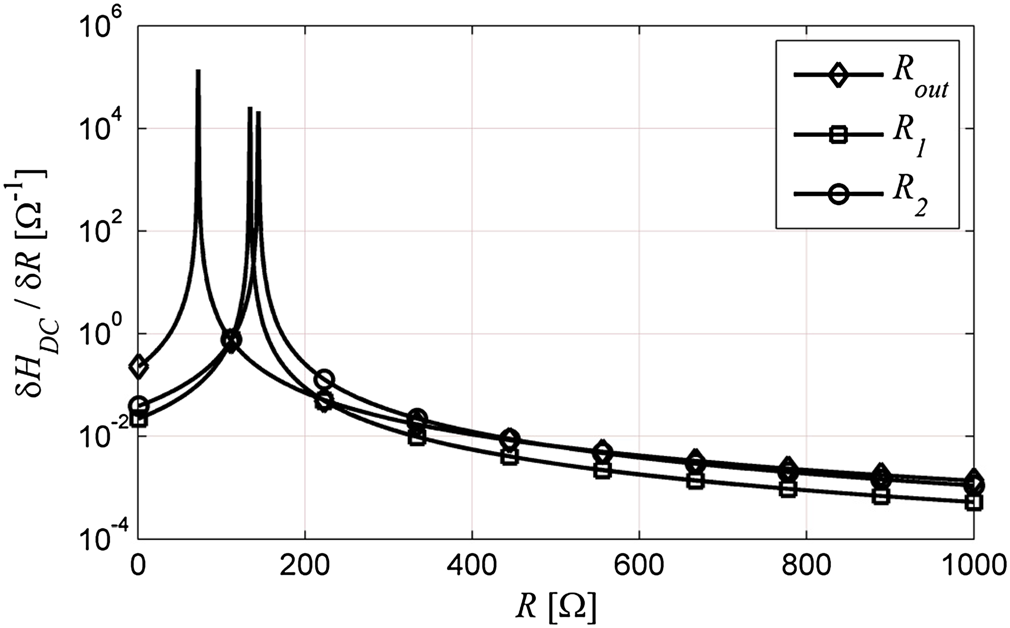
利用(6)，可以定义HDC的灵敏度。HDC对每个变量的偏导数是衡量闭环增益对该变量灵敏度的简单指标。该分析得到以下五个方程：

$$
\frac{\partial H_{DC}}{\partial A_{DC}} = \frac{G_{out} (G_1 + H_{DC} G_2)}{\Psi}
\tag{27}
$$

$$
\frac{\partial H_{DC}}{\partial R_{in}} = \frac{G^2_{in} (G_2 + G_{out}) H_{DC}}{\Psi}
\tag{28}
$$

$$
\frac{\partial H_{DC}}{\partial R_{out}} = -\frac{G^2_{out} [A_{DC} G_1 - H_{DC} (G_1 + G_{in} + G_2 (1 - A_{DC}))]}{\Psi}
\tag{29}
$$

$$
\frac{\partial H_{DC}}{\partial R_1} = -\frac{G^2_1 [G_2 + A_{DC} G_{out} - H_{DC} (G_2 + G_{out})]}{\Psi}
\tag{30}
$$

$$
\frac{\partial H_{DC}}{\partial R_2} = -\frac{G^2_2 [G_1 - H_{DC} (G_1 + G_{in} + G_{out} (1 - A_{DC}))]}{\Psi}
\tag{31}
$$

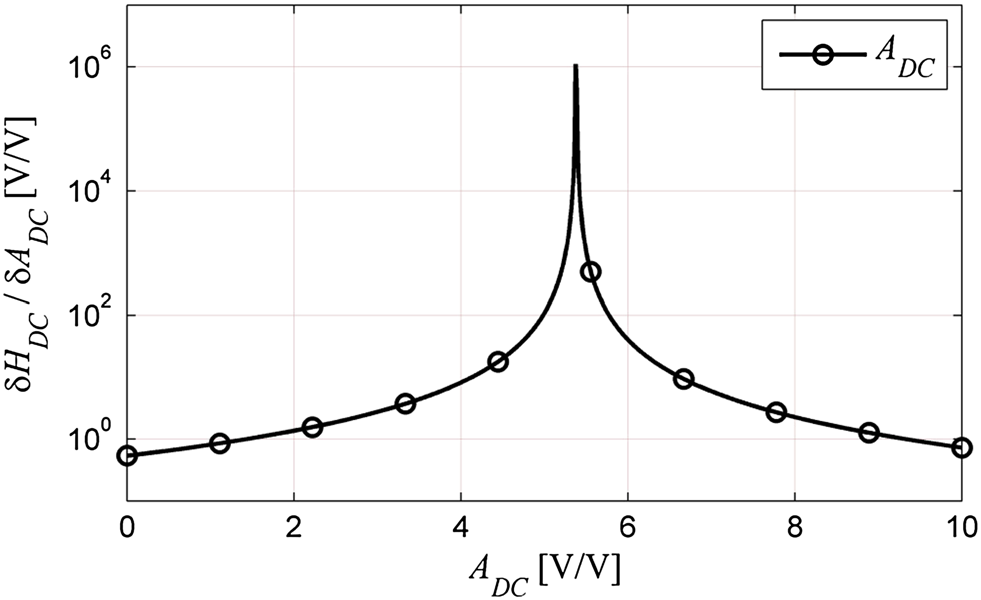
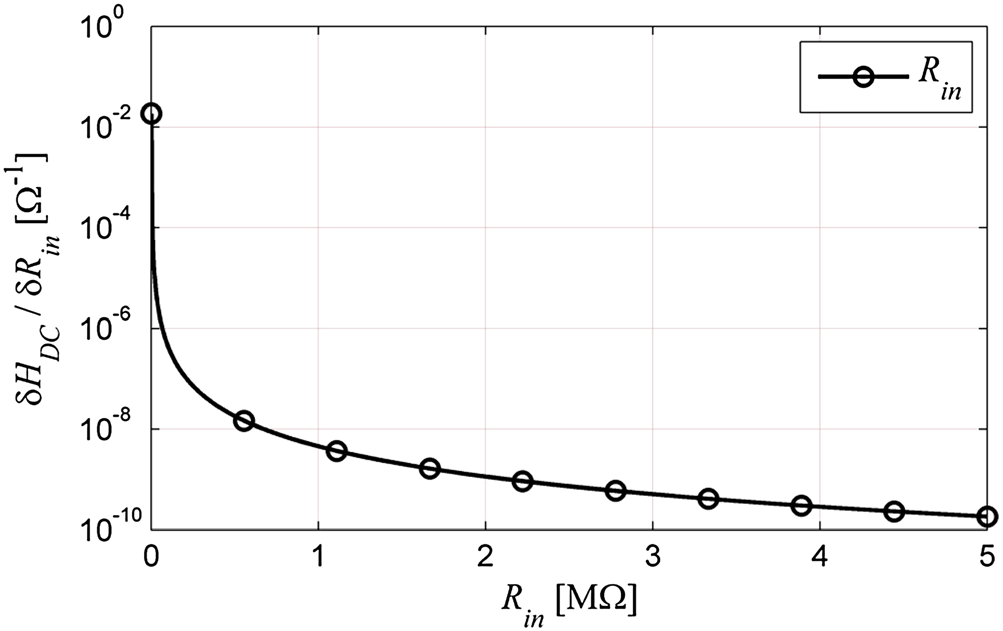
当 Ψ趋近于零时，(27)至(31)达到最大值。在与正反馈方法一致的设计点处进行评估时，(27)至(31)得到的结果如图7、图8和图9所示。这些图形使用参数ADC= 4.271、Rin= 3.76 MΩ、Rout= 182.9 Ω、R1= 100 Ω和R2= 255 Ω绘制而成，并显示出在Ψ= 0附近的灵敏度增强。由于 Rin的幅值相对于其他阻抗较大，因此对该参数的灵敏度很小。然而，其他灵敏度的幅值相近，在实现鲁棒放大器设计时必须给予同等关注。

4. 应用

此处描述的正反馈方法最适用于直流增益较小且带宽较高的放大器。所提出的技术应应用于满足这些条件的电路。基本差分放大器级满足这些条件，并且具有可同时访问正输出和负输出以用于反馈的额外优势。图10(a)显示了基本差分级，图10(b)显示了带有差分正反馈的基本差分级。该放大器采用台积电65纳米逻辑工艺设计和制造，仅使用薄氧化层标准阈值电压器件。设计了无反馈的基准放大器以及两个正反馈放大器。正反馈通过多晶硅电阻实现，其中 R1= 100 Ω固定，R2= 255 Ω和 305 Ω采用两个不同值。采用1 V电源电压的基准放大器的仿真特性为A_DC= 4.271，Rin= 3.76 MΩ，Rout= 182.9 Ω，以及p1= 4.08 GHz。

4.1. S参数测试平台

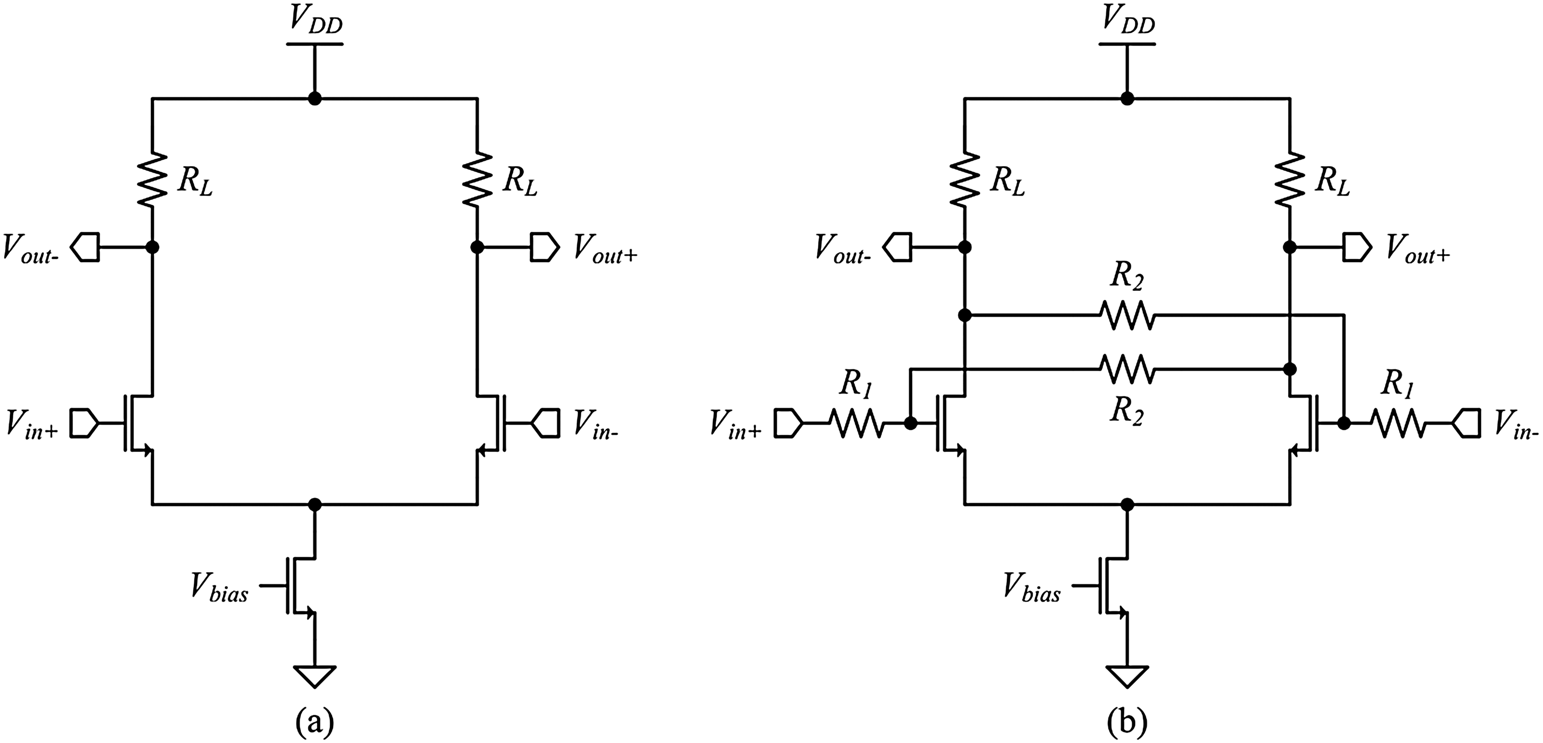差分级 (b) 带正反馈的差分级。)

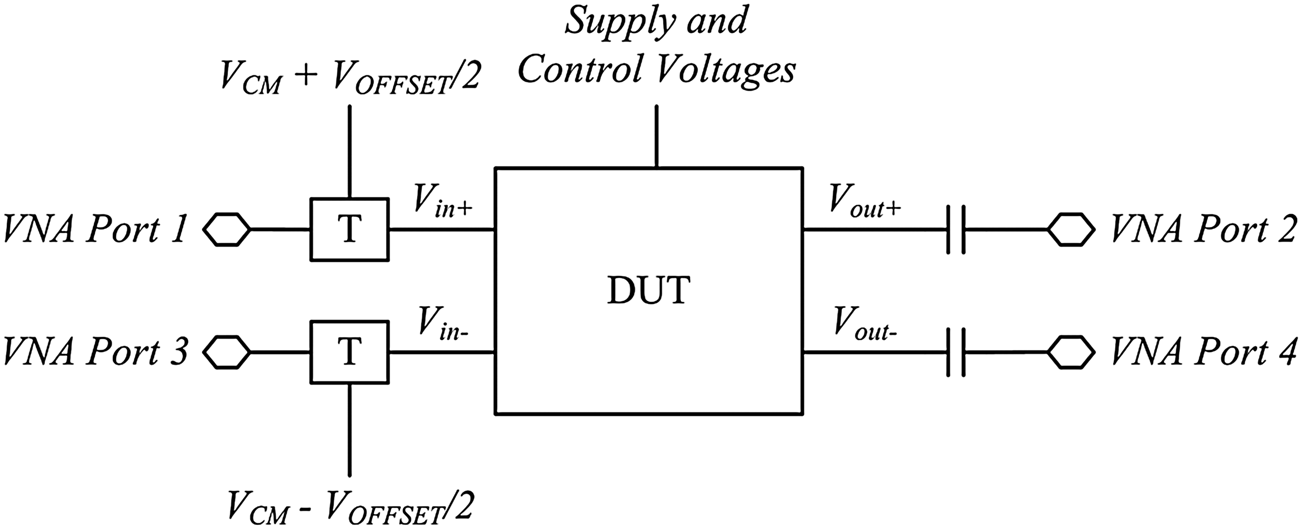
图11 是本研究中使用的S参数测量测试平台的框图。采用安捷伦E5071C四端口矢量网络分析仪(VNA)进行并采集S参数数据。电源电压和控制信号通过HP4156A精密半导体参数分析仪提供。HP11612A偏置T型接头用于向放大器输入端提供直流共模电压V_CM，而SD3244 0.1–18GHz直流隔离块则用于放大器输出端以防止矢量网络分析仪对放大器输出端产生 50 Ω——这种 50 Ω负载效应会影响放大器在阻性正反馈配置下的输入VCM。

四端口S参数测量是在对数尺度下，使用E5071C在50兆赫至8.5吉赫范围内采集的。为了从这些四端口参数中获得有意义的放大器数据，需将其转换为混合模式S参数，如[9]所示。

混合模式参数通过差分和共模输入输出来描述放大器的行为。差分‐差分混合模式S参数Sdd被用于通过关系式[10]评估放大器的电压增益。

$$
A_V = \frac{S_{21} (1 + \Gamma_L)}{1 - S_{22} \Gamma_L} + \frac{S_{11} (1 - S_{22} \Gamma_L) + S_{21} \Gamma_L S_{12}}{}
\tag{32}
$$

其中，AV为电压增益，S11, S12,S21, S22为混合模式S参数， ΓL为负载反射系数，在本分析中假设为0（无负载）。这些测量是在一系列VCM值范围内进行的。图11中的测试平台还具备通过在放大器输入端添加固定偏移来手动补偿因器件失配引起的输入参考偏移的能力，从而进一步优化增益测量结果。为了保持规定的VCM，将偏移电压VOFFSET的一半以相反方向分别施加到两个端子上。

除了放大器结构外，还创建了开路和短路结构，以去嵌入测试设置、焊盘和布线寄生参数。这是一种常用且众所周知的技术[11]，用于将测试设置与被测器件的行为解耦。

4.2. 硅基测量与结果

在台积电65纳米技术下制造的放大器的显微照片如图12所示。该放大器的分析过程包括以下步骤：

1. 测量并存储“开路”结构的S参数
2. 测量并存储“短路”结构的S参数
3. 在给定的VCM和VOFFSET值下，测量四端口S参数
4. 去嵌入寄生参数
5. 将被测器件S参数转换为混合模式S参数
6. 计算电压增益AV

对多个VCM和VOFFSET值重复此分析，以找到放大器的最大增益工作点，如下所示：

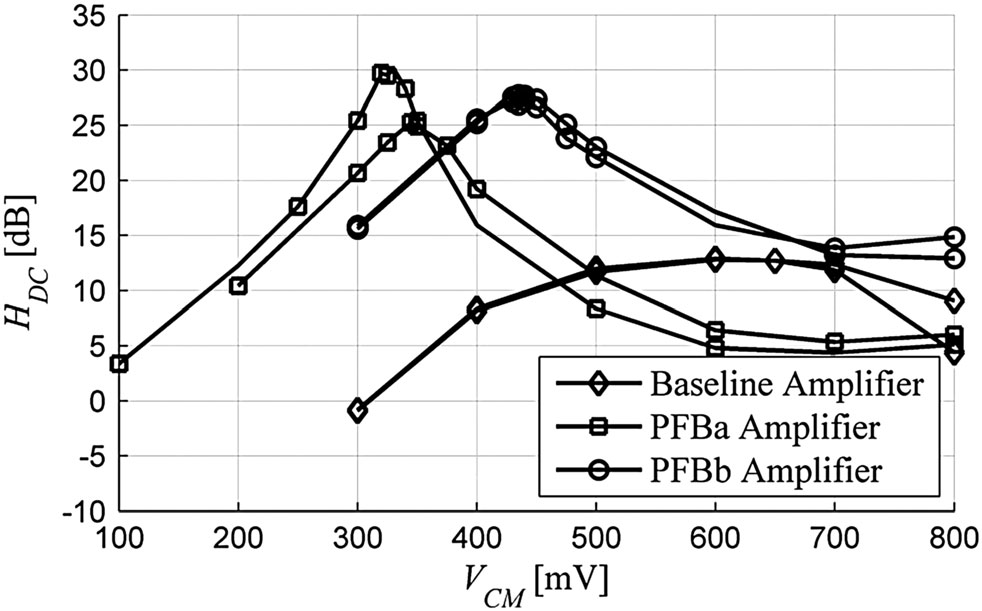
1. 进行了VCM扫描，并分析数据以确定在给定放大器下使直流增益最大化的VCM电压。参见图13作为参考。
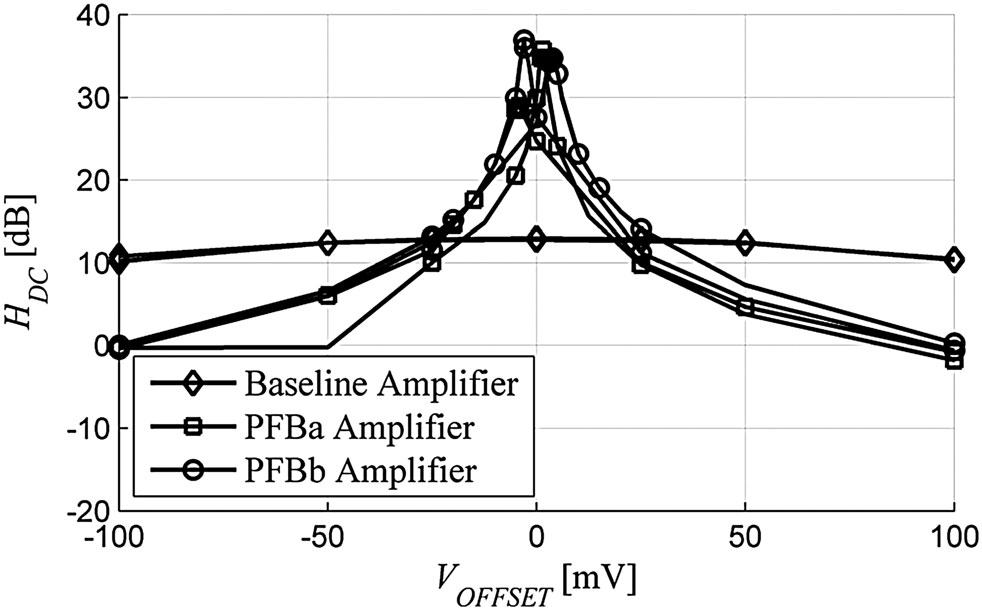
2. 在优化的VCM电压下，进行了VOFFSET扫描，以补偿输入参考偏移并进一步精确化最大直流增益的测量。参见图14作为参考。

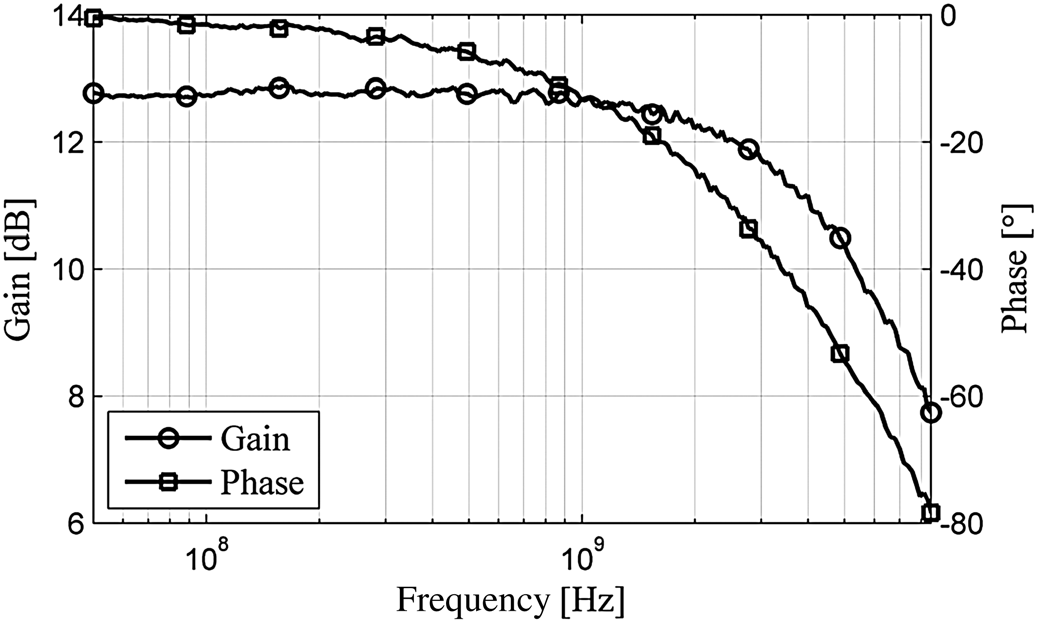
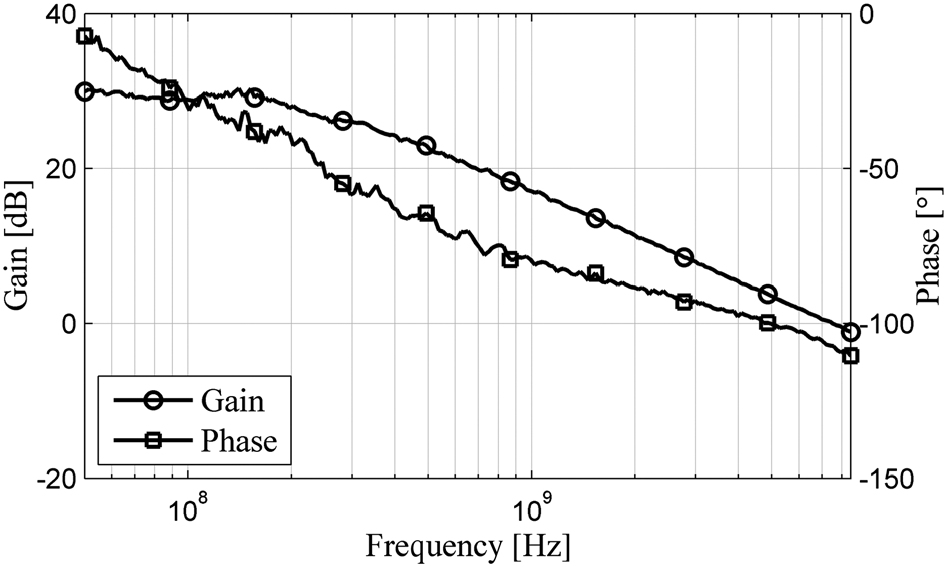
在优化的VCM和VOFFSET下，观察放大器的频率特性。图15和图16分别显示了基准放大器和正反馈放大器在各自最佳VCM和VOFFSET下的频率响应。

该分析共针对15个放大器进行，每种放大器类型各五个：基准、低R2(PFBa)和高R2(PFBb)。这些测量的汇总结果如表I所示。

表I. 直流增益测量。	最小值（dB）	最大值（dB）	平均值（dB）
基准	12.5	13.0	12.7
R2 = 255Ω	27.0	35.0	29.8
R2 = 305Ω	27.0	39.2	34.7

5. 讨论

硅基测量结果显示，正反馈放大器的直流增益值相较于其基准放大器有显著提升。图13展示了每种版本的两个示例芯片。在广泛的VCM值范围内，PFBa和PFBb的增益均高于基准放大器。虽然一个PFBa芯片的增益高于PFBb芯片，但也可以看出PFBa的直流增益分布比 PFBb更宽。这是由于当R2导致 Ψ接近零时，HDC的灵敏度增加所致。

图13还显示了放大器工作在高增益区域时输入共模电压范围减小。这是因为施加到正反馈放大器的VCM与内部基准放大器所感知的电压不同。电阻反馈导致嵌入式基准放大器的VCM随着输入VCM和放大器输出VCM的电阻平均值而偏移。

图14 显示正反馈放大器可以在其输入端容忍更小的直流偏移。对于具有更高直流增益的放大器来说，这是预期的现象——随着输入偏移的增加，输出电压会更快地在电源电压处饱和，从而降低放大器的表观直流增益。在需要容忍输入偏移的应用中，必须考虑输入端折算的偏移消除方案。

如果正反馈放大器将用于如[8]所示的闭环系统中，则必须对偏移进行补偿。

利用图15和图16中的数据，还可以估算正反馈对频率响应的影响。采用单极点近似方法，放大器的 −3dB带宽可测量为相位偏移达到 −45°时的频率。基准放大器的带宽约为5.5 GHz，对应的估计单位增益带宽积为23.8 GHz。然而，正反馈放大器的增益带宽积约为8.5 GHz。这对应于GBPr为0.357，与本文理论预测的显著降低一致。

6. 结论

本文提出了一种将正反馈作为提高放大器增益方法的通用模型。针对正反馈放大器模型，推导了在保持系统稳定的前提下可增加增益的反馈系数的有效范围，该范围适用于实际的放大器拓扑结构。最后，该技术被应用于台积电65纳米工艺中的低增益差分级，仿真结果显示增益提升了14.64 dB，硅基测量结果表明在高达8.5吉赫的频率下增益最高可提升26.7 dB。然而，这种增益的提升伴随着代价，硅基测量显示增益带宽积（GBP）降低了约65%。

与任何设计方法一样，使用正反馈时也需要考虑权衡。如果将正反馈过度应用于放大器拓扑结构，可能会产生增益带宽积退化、输入共模电压敏感性和输入偏移敏感性等意外效应，从而限制放大器工作条件，降低放大器实用性。然而，若将其作为增益增强技术来应对增益退化，而非全面的解决方案，则可在显著提升放大器性能的同时避免这些意外副作用。

考虑到这一点，本工作可应用于高速I/O电路，例如电流模式逻辑，甚至可用于MIPI的 DSI或高通的MDDI物理层设计中的高速数据接收器。这些协议需要在高速、高性能、低功耗和小面积之间取得平衡，而这种正反馈方法的优势恰好能够满足这些需求。