统计学在地区健康问题中的应用

2 统计学对理解地区健康问题的贡献

“统计学对疾病提供了真实的反映，但对患者却呈现出一幅虚假的图景；它在总体上是正确的，但在个体上却是不准确的。”——莱昂·施瓦岑贝格

2.1. 统计学：对现象理解的历史性贡献

本章旨在探讨统计学与数据分析在理解地区健康问题方面的贡献。

尽管本章的讨论基于使用统计方法的示例，但并非对该领域所有现有技术进行全面详尽的概述；这样的讨论足以写成一本书甚至更多。在本泽克里看来，数据分析是从数据矿石中提取真实本质的纯钻石的工具 [BEN 76]。

统计学是一套旨在收集、处理和解释个体或空间单元上的观测数据的方法，这些数据可以是定性或定量数据。其目的是为现象提供解释，对这些现象进行建模以帮助理解它们的演变过程，同时也用于理解一组参数（解释变量）对某一特定变量（被解释变量）的影响因子。

然而伊奥安尼迪斯在2005年指出，超过50%的研究论文结论存在错误发表在医学领域的论文中有许多是错误的，这可能归因于多种原因：科学方面（缺乏能力[，尽管由于同行评审过程，这种情况相当罕见]）、初始错误以及a posteriori错误的风险、人为偏见或对流行理论的盲从和/或经济利益[IOA05]。

统计学包括两大类方法：描述性统计（自14世纪以来已开始使用）和基于概率论的推断统计（始于17世纪），后者用于将从特定样本中获得的统计结果外推至整个总体。

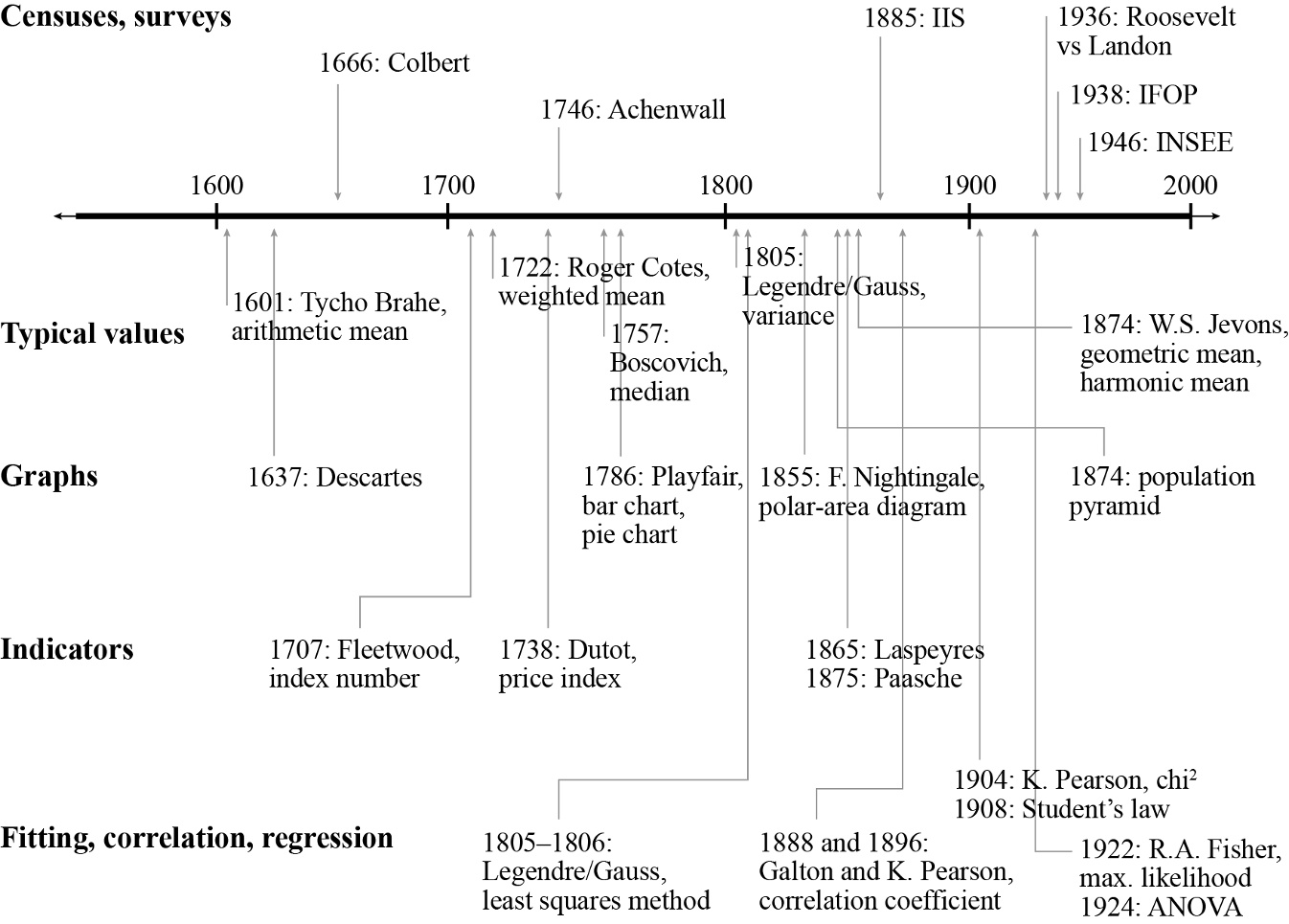
图2.1 展示了统计学从公元1600年至今在历史中的时间发展脉络。

除了标明各种统计方法的位置外，该图还表明许多非常古老的技术至今仍在使用，并未因算法技术的发展而被淘汰。因此，该时间线上的几乎所有技术至今仍被写入教科书并在大学课堂中讲授；它们构成了新方法得以建立的方法论基础。

描述性统计涉及大规模收集数据以构建信息（统计参数、指标），表示这些信息（例如以图表或图形的形式），并将其与参考值（均值、中位数等）进行比较。统计学的优势在于其方法不依赖于特定学科；只要有足够体量的数据，统计学便可应用于任何领域。通常，这些方法包括测量一组单位（人、空间等）共有的特征，尤其是出于匿名性考虑（保护参与者的个人隐私）。

从历史的角度来看，描述性统计近年来不断发展，如今我们已拥有处理大数据的方法（异构数据分析、数据挖掘）；在此范畴内，主要有两大类方法——这些方法在大学的统计学课程中均有教授。我们可将分类方法与因子分析方法区分开来。正如埃尔加泽尔指出的，数据挖掘是一种对原始数据进行操作的自动化过程，其本身属于一个更为复杂的过程，贯穿从数据到信息、再从信息到决策的全过程。[…]总体而言，“数据挖掘要么是描述性的，要么是预测性的：描述性（或探索性）技术旨在揭示存在于数据中但被海量体量所掩盖的信息。例如个体自动分类（聚类）和产品关联搜索就属于此类。而预测性或解释性技术则旨在基于已观测到的信息推断出新的信息（如聚类和预测）” [ELG 07]。

如今，数据挖掘结合基于随机学习过程和非参数模型的完整方法，提供了足以以其独特方式解释大量以往未能理解现象的能力 [CAR 12]。因此，得益于数据挖掘，统计推断的层次已超越了变量选择这一层面，而变量选择正是当今数学研究中最重要的方向之一 [BAR 09]。

聚类方法旨在通过将个体划分为称为聚类的同质群体，从而减小样本的规模。每个聚类包含数量不等但具有相似特征的个体。这类方法主要包括划分和层次聚类法（HAC）。

自动分类（聚类）是一种数学数据分析方法：为了便于研究较大的有效总体（患者、问题等），将数据划分为若干个聚类，使得同一聚类内的个体尽可能相似（组内方差小），而各聚类之间尽可能不同（组间方差大），并反复迭代直至获得树状图；该树状图可用于：一是逐步观察数据的聚类过程，二是估计数据聚类的合适类别数量。由n个变量（成分）Mi(x1,…, xn)和Mj(y1,…, yn)定义的两个个体之间的接近程度，传统上通过两点之间的欧氏距离来估计，其计算公式如下：

$$
d(M_i, M_j) = \sqrt{\sum_{i=1}^{n}(x_i - y_i)^2}
$$

当处理噪声数据或周期性数据时，这种距离度量并不合适。

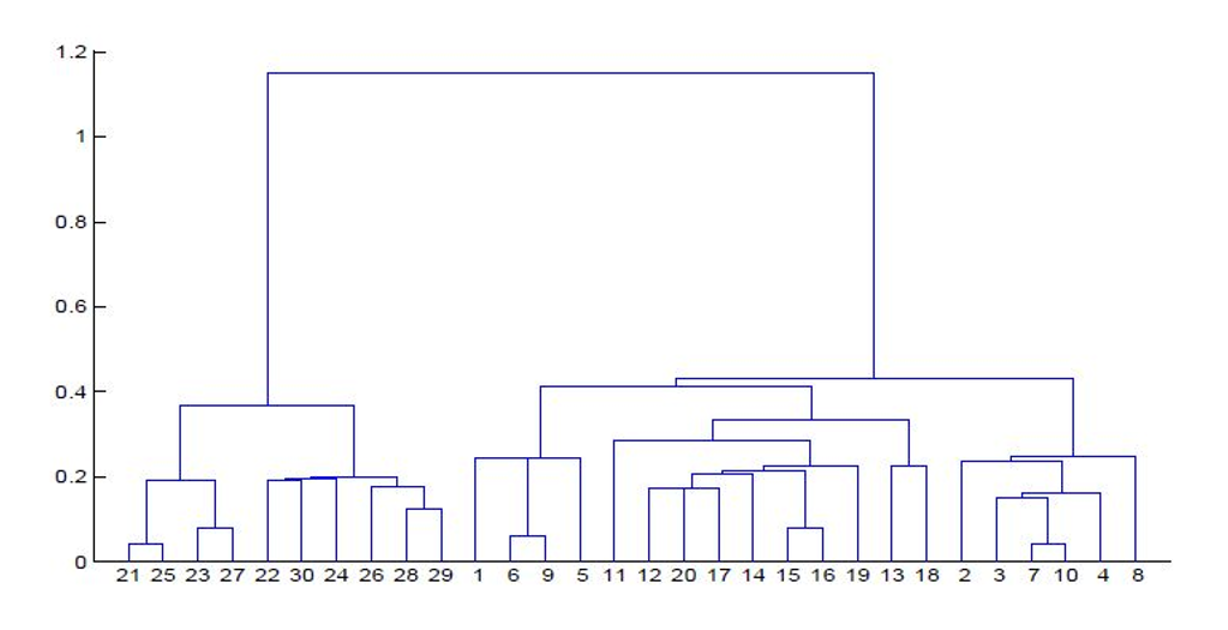
在图2.2所示的例子中，我们可以在树状图中区分出多个层级（1–9，最大分支）。例如，个体7和10是相似的（属于同一聚类），同样地，个体21和25也是相似的。通过回溯树状图（按包含关系组织的类别聚类），最终我们会得到一个包含整个样本的单一类别（此处为29个个体）。该算法是凝聚的；它首先基于非常相似的个体，然后逐步构建出同质性逐渐降低的聚类，直到获得包含所有个体的最终聚类（层次聚类法（HAC））。同一聚类内的对象尽可能同质（组内方差小），而不同聚类之间的对象尽可能异质（组间方差大）。具体来说，在实施层次聚类法（HAC）时，我们分为四个步骤进行：初始聚类为各个个体；计算聚类间距离；将距离最近的两个聚类合并为一个聚类；最后，重复此过程，逐步进行，直到获得一个包含所有观测值的单一聚类。所有这些聚类方法都依赖于所选择的相似性或相异性指标——对于定量或离散变量，该指标通常由一种距离来估计。距离有多种公式化表达。欧氏距离是阶数为α的闵可夫斯基距离的特例，其中 $ \alpha = 2 $，其一般公式为

$$
d(X_i, X_j) = \left( \sum_{h=1}^{m} |X_{ih} - Y_{jh}|^\alpha \right)^{1/\alpha}
$$

当 $ \alpha = 1 $ 时，我们得到曼哈顿距离（也称为城市街区距离）的公式——即基于美国城市街区的一种绕行方式。

福吉于1965年提出了一种称为移动中心法的方法，该方法旨在最小化由质心到其聚类中各点距离之和定义的组内惯性，从而最大化由各聚类质心与总体质心之间距离之和给出的组间惯性[FOR 65]。根据惠更斯原理，我们知道总惯性等于组内惯性和组间惯性之和。

因子分析方法则旨在将总体的大量特征概括为少量被称为因子或因子轴的汇总成分（给出多维点云的轴方向），每个轴都是初始变量的线性组合。

基于由 n 个统计个体（空间单元、个体）构成的数据集，每个个体由 p 个定量变量表征，我们构建一个包含 n 行和 p 列的数据表（矩阵 D）。每一行根据 p 个变量描述一个个体，而每一列则描述一个指标在 n 个个体上的情况。因子分析的目标是将该数据矩阵 D 转换为一个具有 n 行和 p 列（因子）的新矩阵，其中单元格中的值表示个体在不同因子轴上的投影。多维点云的主延伸方向由最能区分个体的成分给出；随后的次延伸方向给出第二个轴，依此类推。根据构造原理，每一对因子轴之间不相关（它们的标量积为零），并且依次解释递减的方差百分比。

第一轴最大化个体的方差，第二轴最大化残差方差，依此类推。

在这些方法中，主成分分析（PCA）能够压缩包含定量数据的多因素表格，而对应分析（FCA）则用于处理定性数据（比较和剖面综合）。

为了确定因子轴，需要进行大量矩阵计算。在对变量进行标准化（通过中心化和缩放操作）后，便可执行矩阵计算。如我们所见，数据矩阵 D是一个具有n行和p列的矩阵。我们将其与矩阵D’相关联，D’是D 的转置。D’与D的乘积得到一个惯性矩阵（方阵且为n阶对称矩阵）。该矩阵用于计算特征值（μ1, μ2,…, μn）以及给出因子轴方向的特征向量。该比值

$$
\frac{\mu_i}{\sum \mu} \times 100
$$

表示各轴上的百分比惯性、方差百分比或信息百分比。该度量指标表明 k轴在区分所分析的个体中的作用。直方图

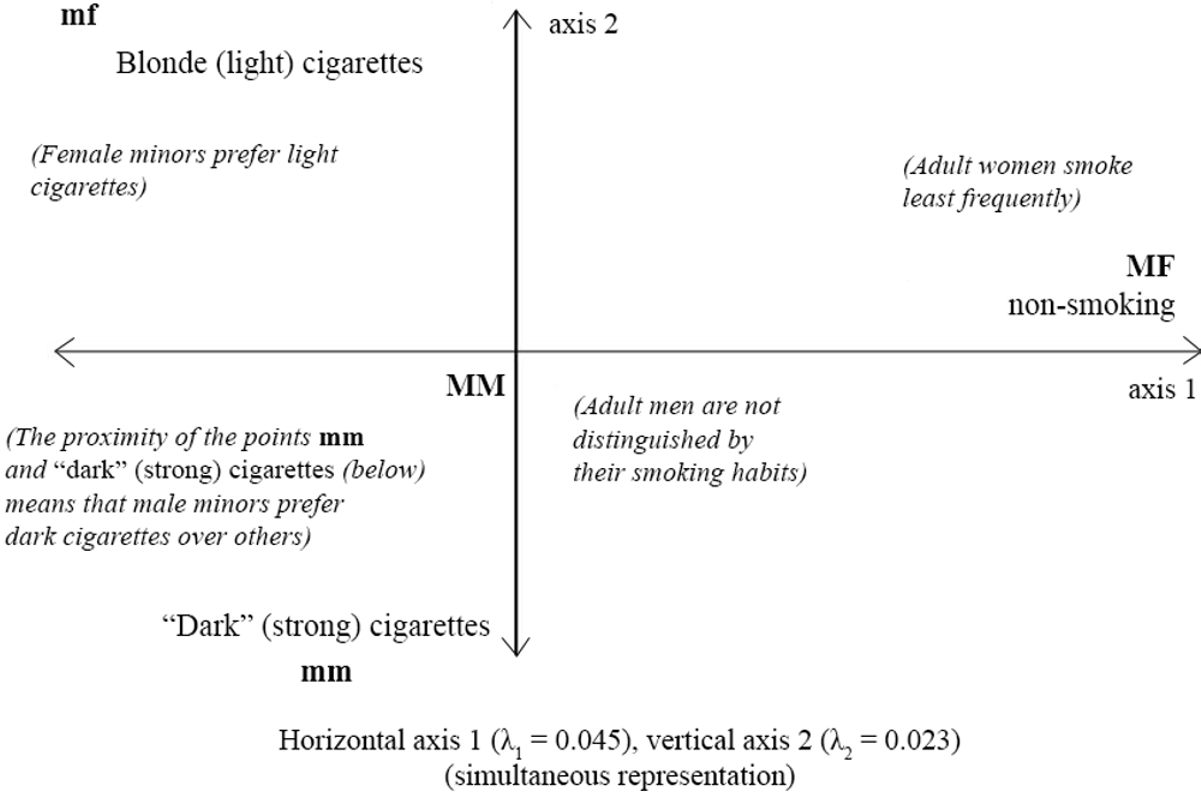
请注意，这些图形表示必须附带“图例/阅读指南”——需要学习才能解释结果；因子轴上点的接近并不意味着个体之间的接近。因此，在因子分析中，通常为每个个体提供四个参数（在各轴上的坐标、表示质量、对各轴形成的贡献、个体在点云总惯性中的作用）；这些参数定义如下。

–个体在因子轴上的坐标 通过分析坐标（或饱和度），我们可以确定个体相对于因子轴的位置，并根据各轴所定义的变量组合来展示个体组之间的相似性或差异。个体在因子轴上的坐标也称为得分或局部权重。这些符号本身无法直接解释，因为轴的方向是任意的。这些符号的意义在于能够体现差异化行为。

–个体在因子轴上表示的质量 两个不同的点在因子轴上的投影可能相同，但其中一个的表示质量会优于另一个——即角度较小的那个。例如，在图2.4中，个体i1的表示质量大于i2 （也就是说，i1更靠近该轴）。表示质量也可以通过观察个体的坐标来估计。表示质量衡量的是到k轴的接近程度。其计算公式如下：

$$
QLT = \frac{d^2(G,Y)}{d^2(G,i)} = \cos^2(\alpha)
$$

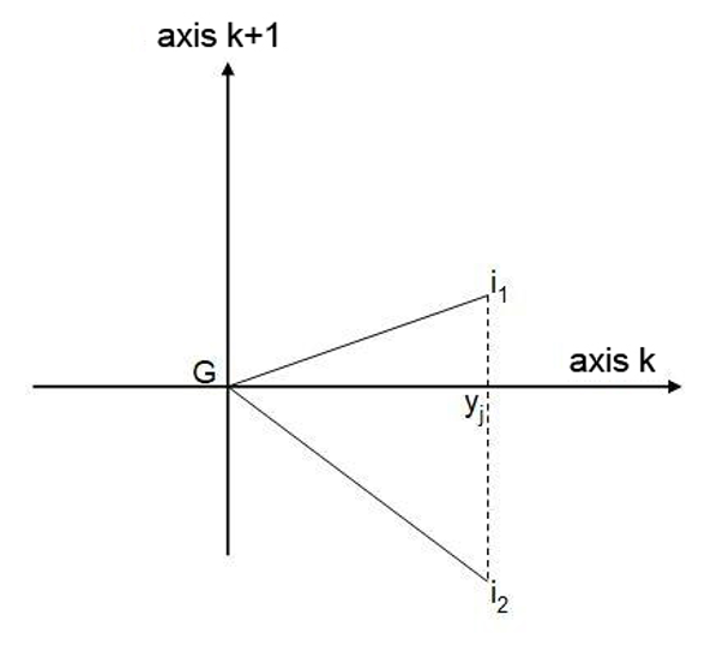
QLT 表示个体 Mi 到重心的距离中被轴k所解释的部分。因此，我们可以确定各个轴在解释个体相对于均值位置时的相应贡献。k 个轴的 QLT 总和必须等于 1（总解释方差）。

–个体对轴形成的贡献 我们使用符号k iCTR来表示个体i对第k个因子轴的贡献。它通过个体i在k轴方差中的作用来衡量。该信息在解释结果时非常有用，尤其是在存在异常点的情况下。

–个体在点云总惯性中的作用 个体在点云总惯性中的作用与其到重心（G）的距离成正比。这使我们能够了解该个体相对于均值的特殊性。如果“I”表示点云的总惯性，则其公式如下：

$$
I = \frac{1}{n} \sum_{ij} d^2(G_{ij})
$$

因此，个体在点云总惯性中的作用表示为Gij到原点距离的平方与总惯性的比值，以%表示。

这四个参数使我们能够正确地评述因子分析的结果。因子轴是所分析变量集的线性组合。变量的饱和度用于衡量其与该轴的关联程度，同时也是该变量的n个标准化值与同一批个体在该轴上的n个得分之间的相关系数。一个轴上所有高饱和度的变量集合用于确定该轴的意义。在解释饱和度和坐标时，我们需要从对立的角度进行思考，从而关注极值。变量越接近零，说明其与该因子的关联越弱。因子轴表达了一种总体结构。某个个体在某一轴上具有正分（投影），并不一定意味着其在所有方面都更突出。实际上，这种显著的位置可能仅相对于一个或两个变量而言（正向和/或负向）

对立可能解释了这一作用。另一方面，一个单极因子（无对立）必须被解释为一种层级结构。为了比较个体，我们需要比较其在多个轴上的位置关系。

主成分分析(ACP)和层次聚类法（HAC）等多维分析方法能够帮助我们整合所研究地区内的全部信息，并提供解读这些信息的关键。基于这些方法，可以构建地区的分类体系，以界定具有相似特征的地区群组。

直到最近，统计学都是描述性的，并基于或多或少完整的数据库。为了克服许多情况下数据库不完整且存在空白的问题，人们开发了一种不同的方法。

统计学的第二个分支是推断统计，其公式化表达基于概率。因此，当样本被正确记录时，我们可以通过基于样本计算出的统计量来近似总体的理论（概率性）特征（概率定律）[MAU 12]。正如法国哲学家莱昂·布伦施维格所说：“认知即测量”。测量可用于发现和描述某种关系——例如，心血管风险与烟草之间的关联；也可用于判断某种药物是否有效（实验组与对照组的比较）。需要记住的是，统计推断是依据最可能的关系来推导行为模式，但它只是众多可能结果中的一种——特别是那些在统计上难以理解的突发情况现象，其不可预测性可能会带来重大后果。

例如，在心脏病发作或心肌梗死的情况下，医疗救治前的预期寿命估计约为10分钟，具体时间取决于梗死类型和患者类型。在发生心脏骤停的情况下，若未进行心脏按摩和/或除颤，每过一分钟生存几率下降10%。平均而言，急救服务到达受害者现场需要13分钟，这解释了目前观察到的低存活率（低于5%）。统计数据显示，心肌梗死后10年，如果没有复发，患者的预期寿命可恢复到从未经历过心脏病发作的人的水平（恢复力现象）。大量研究（如APHEA）表明，高浓度颗粒物与心率变异性降低、动脉
血管收缩、血压升高、血浆黏度增加和心律失常。这些疾病可能导致住院和死亡率增加 [STO 07]。

在统计建模中，特别是当我们考虑多元回归方法时，回归变量或因子之间存在相关性。线性回归相较于其他方法的一个优势在于，它基于概率论，并能提供伴随其不确定性程度的预测。其中最显著的是p值，通过将p值与预设阈值（通常为5%）进行比较，我们可以根据统计检验的结果得出结论。如果p值低于该阈值，则拒绝零假设并采纳备择假设，检验结果被判定为“统计显著”。反之，如果p值高于该阈值，则不拒绝零假设，且无法就所提出的假设从该检验中得出任何结论。

被解释变量表示为p个解释变量的或多或少复杂的函数，并通过一个代表随机因素的因子进行调整：

$$
Y = f(X_1, X_2, ...., X_p) + \varepsilon
$$

关于该因子，皮埃尔‐西蒙·拉普拉斯提到了我们无知的总和——换句话说，就是我们无法用模型解释的部分：即尚未可解释的部分。

函数f不一定是线性函数。例如，在胎儿生物测量中，许多作者研究了胎儿体重估计，并提出了包含一个或多个参数的方程。因此，Weiner et al.指出，以克为单位的胎儿体重（FW）估计值由以下方程给出，其中CP表示头围（厘米），AP表示腹围（厘米），FL表示股骨长度（厘米）[WEI 01]。项1.6961对应于随机性——现象中未被解释的部分。

$$
\log_{10} FW = 1.6961 + 0.0225 \cdot CP + 0.0164 \cdot AP + 0.0644 \cdot FL
$$

其他确定性模型已被建立。第一个模型来自1975年，由坎贝尔以公式形式提出，其形式为（单个超声参数模型）：

$$
\log_e FW = 4.564 + 0.282 \cdot AP - 0.0331 \cdot AP^2
$$

10年后，哈德洛克提出了一个包含两个超声参数的模型：

$$
\log_{10} FW = 1.304 + 0.05281 \cdot AP + 0.1938 \cdot FL - 0.004 \cdot AP \cdot FL
$$

然后是一个包含四个参数的模型：胎儿体重（FW）、头颅周长（CP）、股骨长度（FL）和双顶径（BPD）[HAD 85]:

$$
\log_{10} FW = 1.3596 + 0.0064 \cdot CP + 0.0424 \cdot AP + 0.174 \cdot FL + 0.00061 \cdot BPD + 0.00386 \cdot AP^2 - 0.00061 \cdot AP \cdot FL
$$

将不同模型的结果与实测出生体重进行比较表明，相关性最好的方程是采用三个参数得到的；误差通过以下公式计算：

$$
\text{Error(\%)} = \frac{\text{Estimated fetal weight} - \text{Newborn weight}}{\text{Newborn weight}} \times 100
$$

在健康领域，统计学被应用于医学影像、流行病学、诊断、临床试验等方面。其目的是比较多种治疗方案的有效性，并将统计证明的概念引入医学。对临床试验感兴趣的读者可以参考该主题下已发表的大量著作——尤其是埃马纽埃尔·沙莫雷关于肿瘤学中早期阶段测试方法论的博士论文：[CHA 09]。在疾病方面，统计学几乎总是用于已诊断疾病的情境，而非疑似病例，尽管也可以考虑采用概率统计方法。

经典统计工具可分为两大类：集中趋势原理和概率理论。集中趋势模型（如最小二乘回归）旨在寻找响应变量与一个或多个预测因子之间的关系。例如，我们可以尝试通过个体大小来调整权重（交叉引用定量数据的模型）。当我们希望将一个变量解释为多个其他变量的函数时，该方法类似于经典线性回归。

其他模型，例如方差分析（ANOVA），可用于将一个定量变量解释为一组定性变量的函数；这些模型已通过显著性检验得到验证，使我们能够接受或否定某一假设。让我们来看一下方差分析模型的工作原理。方差分析（ANOVA）是一类可用于比较多个样本的方法。该分析涉及检验由解释变量定义的每个组（或样本）内的变异差异是否在所有解释变量整体上显著不同于0。具体而言，我们首先计算总样本量为n的总方差，然后计算组内方差和组间方差。根据这两个值，我们推导出实验F值，即组内方差与组间方差之商。接着，我们计算该问题的自由度（dof），并提出所谓的零假设（H0），即各个样本（k）的均值相等。因此，我们共有kn个测量值，来自k个大小为n的样本。将实验得到的F值与费希尔‐斯内德科尔表给出的F值进行比较，该表格具有双重输入参数，分别为样本数减一（k − 1）和总测量数减k（nk − k = N − k）。需要注意的是，当样本服从符合拉普拉斯‐高斯定律的分布时，并非必须执行所有这些计算，但这种情况并不总是成立。

变异	平方和	自由度	均方	F
Intra	$SC_{intra} = \sum_j n_j (X_j - \bar{X})^2$	$k - 1$	$MC_{intra} = \frac{SC_{intra}}{k - 1}$	$F = \frac{S^2_{inter}}{S^2_{intra}}$
Inter	$SC_{inter} = \sum_{i,j} (X_{ij} - X_j)^2$	$N - k$	$MC_{inter} = \frac{SC_{inter}}{N - k}$	拒绝 H₀ 如果 $F \geq F_{1-\alpha; k, N-k}$
总计	$SC_{total} = \sum_{i,j} (X_{ij} - \bar{X})^2$	$N - 1$

表格 2.1. 方差分析方法概述

例如，考虑k种治疗1到k，其中治疗1有n₁个个体，治疗2有n₂个个体，⋯⋯，治疗k有nₖ个个体；令Xᵢⱼ 为第j种治疗的第i个观察值。X̄ⱼ 表示第j种治疗样本的均值，X̄ 表示整个数据集的均值。以下所示的决策算法用于得出结论。

然后，我们可以借助参数“η²”来衡量治疗的有效程度，该参数定义为组内变异与总变异的比值：

$$
\eta^2 = \frac{SC_{intra}}{SC_{total}}
$$

该参数的取值范围为0到1；0表示组内同质性，而1表示最大方差。

当零假设被拒绝时（即各组的均值不同），我们可以检验特定假设以比较不同治疗。如果我们至少有一组的均值与其他组不同，且组数超过三组，则需进一步探究各组之间两两差异。这可通过谢费法进行——一种基于组间对比的检验，该对比定义为组均值之间的差异。

对于任何随机变量，都可以赋予其一个概率，从而定义一个概率定律。当试验次数增加（n趋向于无穷大）时，该现象的观测频率在数学上趋于概率，统计观测到的分布也趋于某一特定概率定律的分布。因此，根据大数定律，我们可以将样本所显示的趋势推及总体。研究人员可以使用多种概率分布，具体取决于所涉及的变量是离散的（均匀分布、伯努利分布、二项分布、泊松分布、负二项分布）还是连续的（均匀分布、正态分布或拉普拉斯‐高斯定律等）。概率有两种类型：所谓频率学派或客观概率，关注的是大量试验中事件的发生，以及统计推断方法（贝叶斯或主观概率），能够重建缺失或不确定的数据。贝叶斯概率至少需要对未知事件（无论是过去还是未来）的先验概率进行近似评估。该先验概率由专家意见给出，从而允许建模者或统计学家引入自身的直觉。而频率主义概率则仅基于后验概率进行操作，即考察过去状态。当我们处理非常大的样本时，频率主义概率与贝叶斯概率会得出相同的结论；而在小样本情况下，只有贝叶斯概率能够产生统计学上显著的要素。

2.2. 关于指标的相关性

当一个指标的数学表达式简单但稳健、普遍可理解（这甚至可以说是其可接受性的先决条件），并且在类似情境下具有可重复性（可转移性）时，该指标的质量更高。

从统计学角度而言，当存在多种影响疾病的因子同时作用时，估计疾病发病率的增加情况具有难度。例如噪音和饮食因素均会影响糖尿病、高胆固醇和肥胖等健康状况，尽管在这种情况下多元回归模型可提供部分分析。此外，还可能存在这样的情形：若干因子单独考察时对健康并无影响，但当它们共同作用时却会产生效应（这被称为鸡尾酒效应）。

鸡尾酒效应可能表现为多种形式：加剧个体效应（协同效应）；出现新的、意想不到的效应（增效作用：某种化学物质本身无明显毒性，但在其他物质存在下被激活）；相加效应；拮抗效应，即一种化学物质的效应被另一种物质的效应所抵消；或独立效应，意味着这些物质彼此之间不发生相互作用。

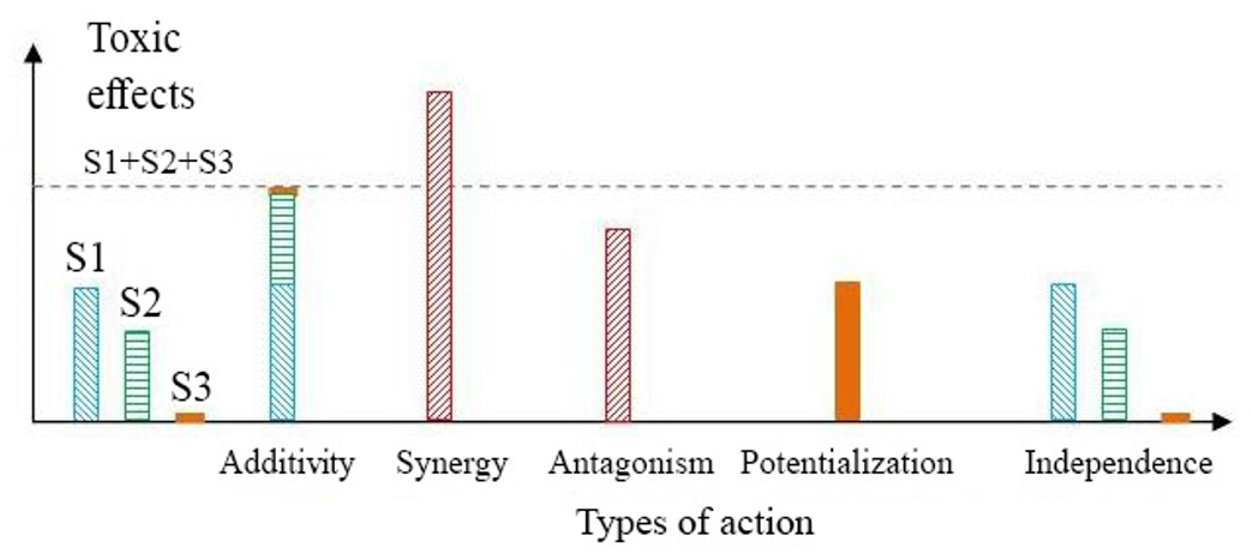
所生成的指标在其公式化表达中，可包含一个或多个静态或动态特征，以及空间或其他性质的特征。例如，如果我们希望衡量气候变化对人群健康的影响，可以考察因热浪频率、强度和/或持续时间的增加所导致的热应激指标，以及随之而来的大体温、中暑和心血管或呼吸系统疾病病例潮[BES 15]。

我们知道，生物体（包括我们自己）只能在相对较窄的热条件范围（最适范围）内生存，因此所采用的统计参数较为简单（平均温度、标准差和置信区间[；]x±σ）。统计学在长时间段内的研究表明，超额死亡率最高的情况与每日最低温度的第99百分位数[BES15]相吻合。

在法国，心血管疾病（CVD）是女性的主要死因 [BAR 16]。这些作者使用Logit‐二项式类型模型，研究了2006年就业的2,780名女性和2,633名男性样本中2010年报告的心血管疾病患病率以及自2006年以来出现的心血管疾病，但未考虑各种混杂因素 [BAR 16]。女性中的结果仅显示对有害产品的暴露程度（OR = 2.36）与至少两种身体压力（OR = 1.98）与心血管疾病声明之间，以及接触有毒物质与动脉高血压之间的关联（OR = 1.54）[BAR 16]。

同样，减少城市环境中的空气污染将对人群健康产生直接的积极影响。欧盟委员会项目Aphekom表明，在25个主要欧洲城市将PM2.5颗粒物浓度降低至年平均值不超过10 μg/m³ （这是世界卫生组织设定的目标值），可使三十多岁的人群预期寿命延长22个月；将延迟19,000例死亡，并实现总货币节省310亿欧元 [PAS 13]。通过交叉比对死亡率数据和气温数据发现，与其它季节性因素相比，寒冷对冬季超额死亡率的影响非常轻微。然而，包括金尼在内的作者已检验了所选统计模型对结果的重要性（模型敏感性分析）[KIN 15]。研究选取了四个城市（巴黎和纽约因其夏季与冬季之间的显著温差，迈阿密因全年炎热潮湿的气候，以及马赛因其属于中间状况），金尼等表明，如果我们不调整季节因素，寒冷的影响似乎远比控制季节效应时更为显著，而高温的影响则显得较弱。因此，当气温升至20°C以上时发生的夏季超额死亡率，明显高于冬季仅在少数几天气温降至0°C以下时观察到的超额死亡率[KIN 15]。作者还针对时间数据进行了敏感性分析，因为寒冷可能具有延迟影响。该研究将日平均气温替换为死亡当日及其前4天共5天的平均气温。此时，低温的影响变得更为显著，但仍然小于高温的影响[KIN 15]。因此，经过时间是一个对结果具有非常重要影响的参数；是否将其纳入考虑甚至可能逆转研究结果，因此所使用的统计模型至关重要。

Dab 等[DAB 01],在其关于15篇文献综述的文章中指出，大气污染与健康之间相关性或因果关系的死亡相对风险尽管具有统计显著性，但程度轻微——通常在细颗粒物含量每增加100 μg/m³时，相对风险一般低于1.1。然而，他们指出了污染数据空间表征的问题；对此，许多作者认为在考虑到个体行为的差异、监测站的选择与位置、浓度的空间变化以及室内空气与室外空气之间的系统性差异的情况下，仅基于少数几个测量站点或仅基于一个测量站点来界定大城市地区总体的暴露情况是存在问题的 [DAB 01]。

2.3. 数据来源：大数据及其在健康领域的应用

正如埃尔加泽尔指出的，健康是一个拥有大量且类型多样的数据的领域（如年龄和性别等典型变量，以及所有医疗干预、诊断等符号变量）。一般来说，数据挖掘包含一系列技术，这些技术要么是描述性的（旨在揭示存在于数据中但被数据体量所掩盖的信息），要么是预测性的（旨在从数据库中已有的信息中推断出新的知识）[ELG 07]。

人们对大数据的兴趣日益增加。当我们查看“大数据”、“云计算”和“Web 2.0”在谷歌趋势中的搜索情况时，可以看到（如图2.6所示），大数据与其他两个术语一样呈现出上升趋势，但存在时间上的滞后：大数据直到最近（2013年）才开始流行起来。

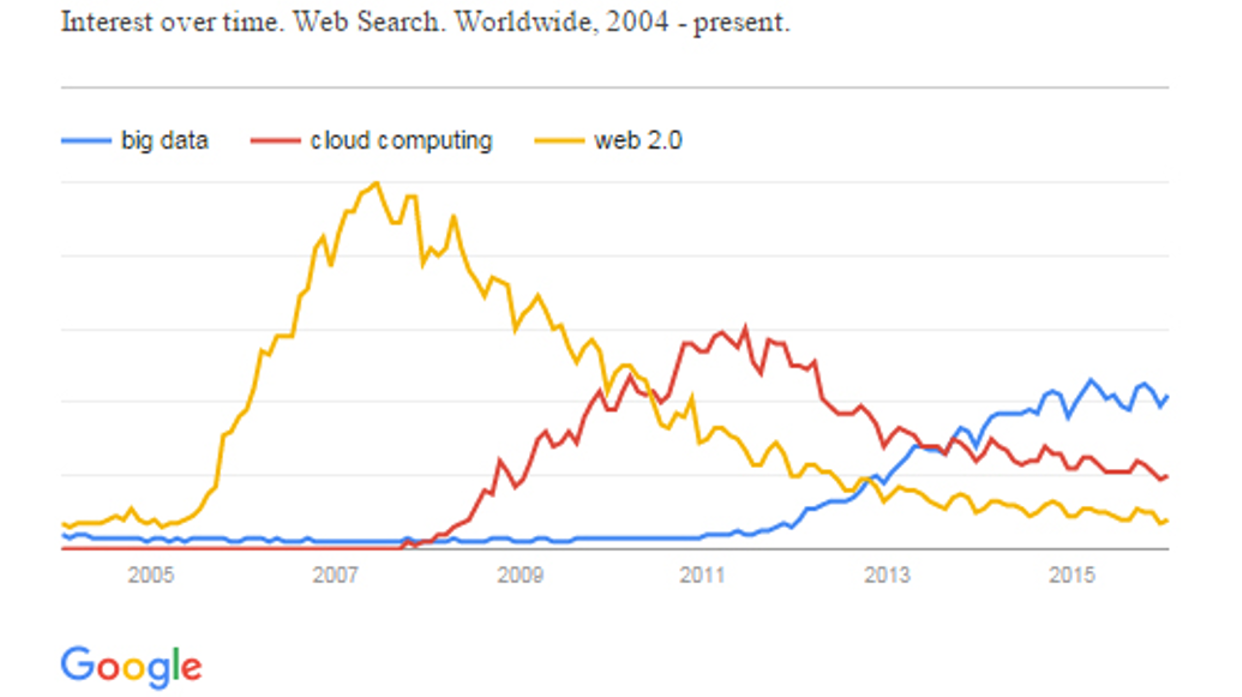
正如迈克尔·巴蒂指出的，在学术文献中关于大数据有众多定义，但其中一个特别能说明其本质：任何无法装入Excel电子表格的数据[BAT 13]。因此，数据与大数据之间的界限并不明确，可能因上下文而异。然而，大数据的问题不能仅仅局限于我们所处理的数据库规模，还必须从不同的数据收集方法、不确定性与可靠性、不完整数据等方面进行分析。大数据考察的是数据的三角链条：生产–处理–使用。这涉及如何让数据彼此互通并赋予意义，同时也包括如何检测微弱信号（极端情况——小数据）。纳西姆·尼古拉斯·塔勒布在其著作《黑天鹅》中提出了两种研究现象的可能方式。“第一种是排除异常情况，专注于‘正常’现象。研究者忽略异常值，仅研究普通案例。第二种方法则认为，要理解某一现象，首先必须考虑极端情况——尤其是像黑天鹅那样具有巨大累积效应的罕见事件”[TAL 12]。这两种方法与统计学中的典型参数（集中趋势和离散程度）非常相似，特别是在考察高斯分布时尤为明显。然而，塔勒布指出，社会生活中几乎所有的事件都是由冲击以及罕见但重大的突发情况所导致的；然而，该领域的几乎所有研究都集中在所谓“正常”的情况下——特别是所谓的钟形曲线（高斯分布）及其检测方法，而实际上几乎无法带给我们任何有用的知识[TAL12]。大数据无疑将迫使我们改变这一范式，通过研究技术、方法和概念上的突破，以更好地应对不确定性。正如古斯塔夫·贝尔韦泽伯爵所说，关于随机变量的不确定性，可以通过熵的概念来度量，“出人意料之事并非不可能；它始终是一张正在使用的牌”。当不存在不确定性时，熵为零。最初，熵是用来衡量封闭系统中无序程度的一个指标。

每天，全世界都会产生2.5万亿字节的数据。世界上存在的90%的数据都是在最近两年内创建的。这就引出了关于4V（体量、速度、多样性和真实性）的问题。哪些数据量需要被处理和存储（上游，以及处理和整合后的下游）？某些流程几乎需要实时（速度）的数据输入。格式和标准的多样性引发了对这些数据结构化和共享方式的质疑。真实性指的是评估对数据本身以及统计、数学或制图模型输出结果的信任程度，这些模型以同样广泛多样的格式生成新的数据或结果。数据安全及其使用是贯穿4V各个层面的重要问题。

在健康领域，大数据是由社会人口学和健康数据组成的一个集合。它们能够帮助我们识别风险因素、辅助诊断、监测治疗效果，并开展药物警戒或流行病学研究。尽管如此，仍存在诸多需要突破的障碍，远不止存储和数字运营能力的问题。事实上，健康数据本质上具有高度异质性，需要进行转换和解释操作。这种异质性体现在多个层面：数据的性质（基因组学、临床、生物、生理、社会等）、数据格式（文本、医疗报告、二维和三维图像、基因组序列、信号），以及通过各类信息系统分布的特点（医院、研究实验室、公共数据库、各种调查）。因此，这些数据具有敏感性，通常经过匿名化处理而有所损失，同时也具有动态演变性（因为相同数据的格式可能逐年变化），这将是下一节讨论的主题。

2.4. 数据对齐问题：可用格式的问题

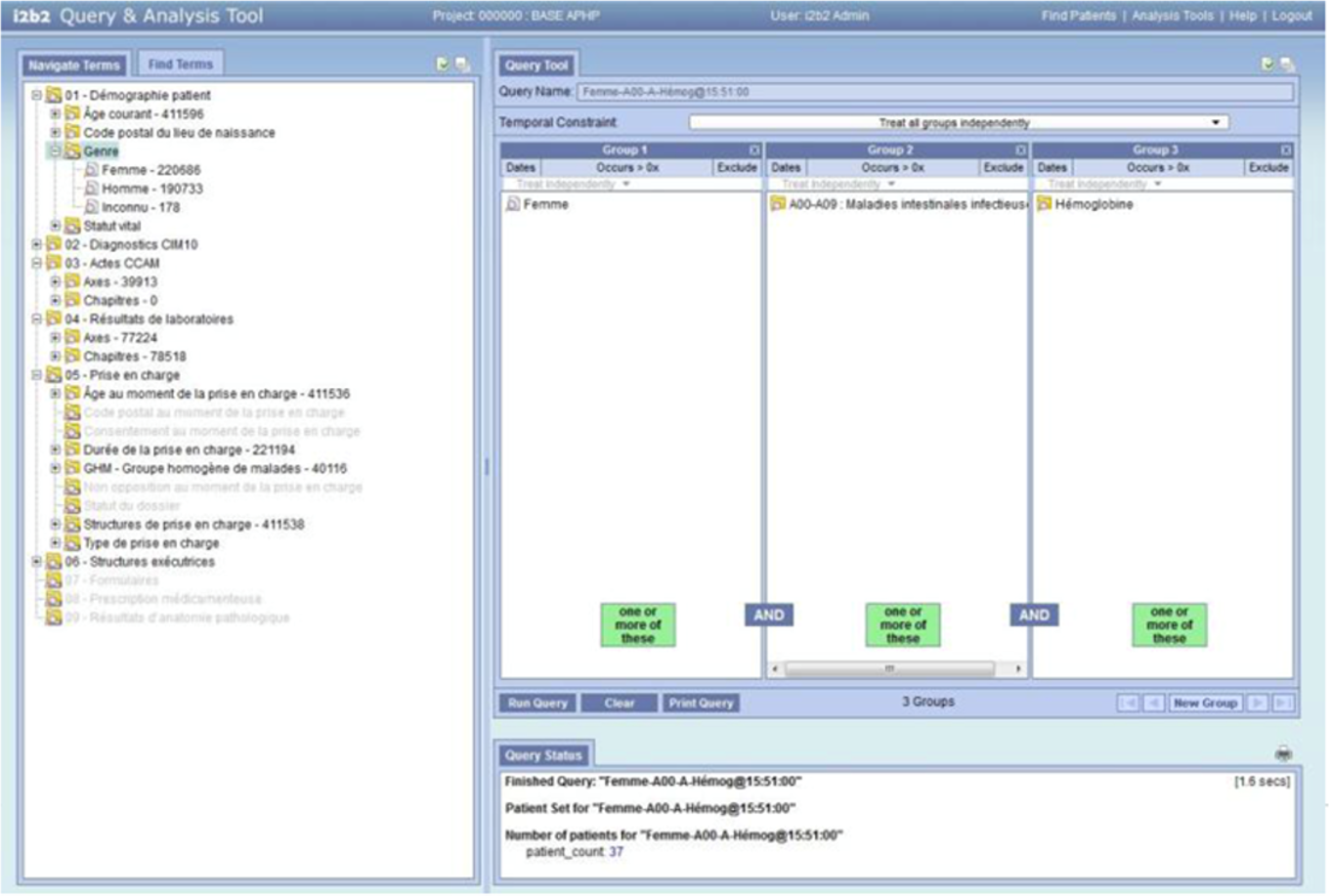
大数据是碎片化的。所收集的信息在以下方面日益呈现异质性：其性质（基因组学、生理、生物、临床、社会等）、格式（自由文本、术语编码、数值、信号、二维和三维图像、基因序列等），以及数据在多个信息系统中的离散程度（医院集团、研究实验室、公共或私人数据库、健康数据持有者）。为了便于处理和利用，这些复杂数据必须以结构化的方式获取，并在输入数据库或数据仓库之前进行编码。该领域正在出现一些标准，例如在波士顿开发的i2b2（整合生物学与临床的信息学，https://www.i2b2.org），目前已在雷恩大学医院中心、波尔多以及巴黎的巴黎公立医院援助中使用。

Ahmed et al. [AHM 17]分析了生物信息学中现有的不同数据模型，并制作了一个比较其各自性能的表格（见表2.2）。在临床数据领域，以及更广泛地说，在患者档案所包含的数据方面，已开发出FHIR标准（快速医疗互操作性资源，可在 https://www.hl7.org/fhir/overview.html 获取），以促进健康信息的电子交换。根据马尔凯斯基 [MAR 17],的观点，虚拟病历、DICOM结构化报告和HL7 FHIR已经改变了医疗数据在机构之间共享的方式，并将成为大数据互操作性的关键因子。

数据模型 (格式)	性能	速度	支持平台
CSV	优于JSON文件格式	慢于序列文件格式	MapReduce/Hive
Text	少于CSV格式	比序列慢文件格式	MapReduce/Hive
序列	更适合小的数据集	小型数据更快大型数据更慢	MapReduce/Hive
JSON	少于CSV格式	比CSV慢格式	MapReduce/Hive
ARFF	比CSV好格式	比序列慢文件格式	Weka
Avro 序列化	少于 Parquet 和 ADAM 最适合多个 rows	比 Parquet 慢 可扩展性较差 许多列	Hadoop MapReduce， HBase、Hive、Pig 和 Spark
Parquet	优于Avro 最适合多个列 少于ADAM 堆栈 不支持索引	比 Avro 更快 对于许多行	Hadoop MapReduce， HBase、Hive、Pig 和 Spark
ORC（优化的 row 压缩）	优于 Avro 支持索引 最佳选择是 Hive	比 Avro 更快 最适合用于查询处理	Hadoop MapReduce， HBase、Hive、Pig 和 Spark 不支持 HBase
ADAM栈	优于简单模式 Avro、Parquet 和 VCF	比简单模式更快 Avro、Parquet 和 VCF	对 Apache 的最佳支持 Spark

表2.2. 不同数据模型（格式）的性能比较

2.5. 数据相关的伦理问题

在科学研究中，存在多种方式来表征健康、环境与社会之间的关系。这种多样性通常被认为是一个优势，因为它鼓励研究人员从多个角度审视复杂问题。Lechopier [LEC 13]阐明了在同一研究项目中，健康与环境两种方法的共存——当它们的概念模型部分不兼容时——可能产生摩擦，而这种摩擦在伦理层面具有重要意义。研究项目中相关人群参与方式的不同、问题各个方面表征的异质性、研究人员责任范围的界定、研究成果知识的合理共享等问题，不应被视为次要问题，而应被视为与方法选择、数据收集工具类型、研究的有效性以及结果的可能推广等议题内在关联的重要内容。为验证一种用于研究氡的存在与环境相关性的动态制图工具，现提供一个个人实例以作说明。

在法国滨海阿尔卑斯省地区胃肠道癌症（医院数据）的患病率与地理环境之间的地理相关性研究中，特定沿海区域的识别问题使我们面临因果关系可能被误读的风险。尽管数据伦理（数据采集和处理）如今已有非常明确的法律框架作为决策依据，但研究成果后续传播和解读的伦理同样重要，研究人员必须时刻保持警惕。类似于数据保护法规的发展以及“设计阶段即考虑隐私”的理念，随着欧洲数据保护条例[CNI14]的实施，在开展“健康—环境”关系研究时，结果的伦理（从而也包括数据处理方式的伦理）也必须在研究设计之初就纳入考量。事实上，除了数据采集和地理相关性统计处理等纯技术层面之外，暴露特征分析（及其在时间和空间上的演变）、所涉总体及个体的脆弱性特征等因素，都是任何关注该研究的人在得出流行病学意义上的因果关系结论时必须充分审慎考虑的关键因素。