向量点乘的图形学意义

向量的点乘是入门图形学的重要基础，本身并不复杂，但因为总与叉乘(图形学前期用不着)放在一起讲，搞得新手都很混乱，本文单独讲解一些点乘的图形学意义，新手先忘掉叉乘吧。

1.向量

向量即空间中的一个点到另一个点。

二维向量

2.向量点乘

向量点乘通常用来描述一个向量在另一个向量的投影分量。

向量点乘的几何意义

向量点乘公式

如上图的映射结果即为点乘结果，因此:
当两个方向向量相等时点乘结果为1
当两个方向向量垂直时点乘结果为0
当两个方向向量相反时点乘结果为-1

原理

3.图形学基础常用的点乘

NDotL

法线方向点乘光入射方向L，通常用来计算基础光照结果
如下图，使用NDotL可以直接得到模型顶点的法线方向与光线方向的结果，越接近1的地方越亮，等于0的地方则不发光，小于0的地方则为暗部。如此即为最基础的“兰伯特光照模型”。

兰伯特光照模型

NDotV

法线方向点乘视角方向V，通常用来计算模型边缘实现菲涅尔边缘光效果
其实与NDotV原理差不多，相机的视角方向与N法线方向点乘结果越小，说明该顶点与视角方向越垂直，则中间越亮边缘越暗，然后按照取值再做一下换算即可获得边缘光效果。

NDotV

RDotV

Phong高光算法：光线出射角的向量R与视角方向V点乘来获取物体的高光值
R是L基于N的镜像反向量(镜面反射)，Phong是最早的物体高光算法

Phong高光算法

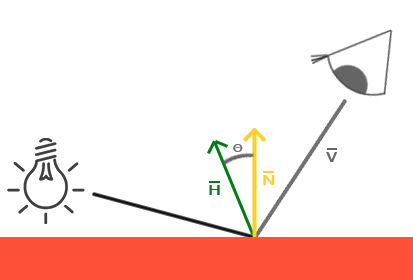
NDotH

法线方向点乘光入射方向L和视角方向V的中间向量，BlinnPhong高光分布，用于简化Phong高光算法
将上述Phong取镜像反向量变成了L+V，简化了计算过程提升了效率，顺带解决了一些Phong算法本身存在的问题参考。

BlinnPhong高光原理