步进电机在高速运行时反电动势波形与其动态响应变化

BEMF的产生：步进电机旋转时，线圈在磁场中切割磁感线产生反电动势（BEMF），其本质是阻碍电流变化的感应电压

1.反电动势波形在高速下的变化

(1) 幅值随转速线性增大

当转速从15 rpm升至30 rpm时，反电动势峰值显著增加。这是因为反电动势公式为E = ke × N × ω（ke​为反电动势常数，N为定子绕组匝数，ω为角速度），转速越高，BEMF幅值越大 。

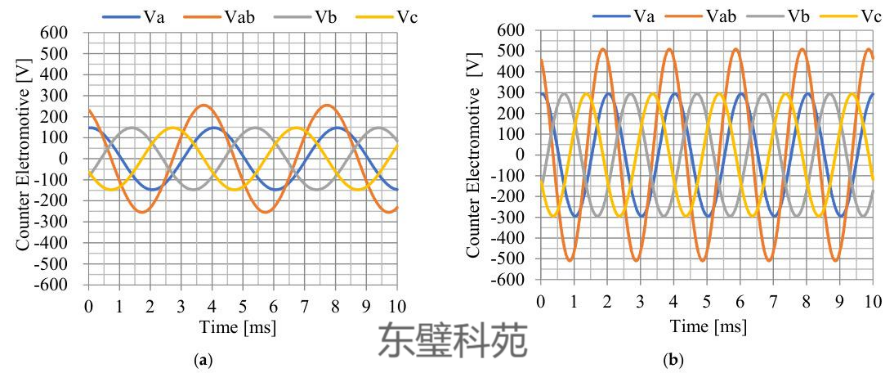
步进电机转子齿数通常为50-100齿（如1.8°步进电机含50齿），相同转速下单位时间磁场切割次数是伺服电机的6-12倍，导致BEMF幅值显著升高。

(2) 波形频率升高，周期缩短

转速从900 rpm升至1800 rpm时，BEMF波形周期数增加，频率翻倍；

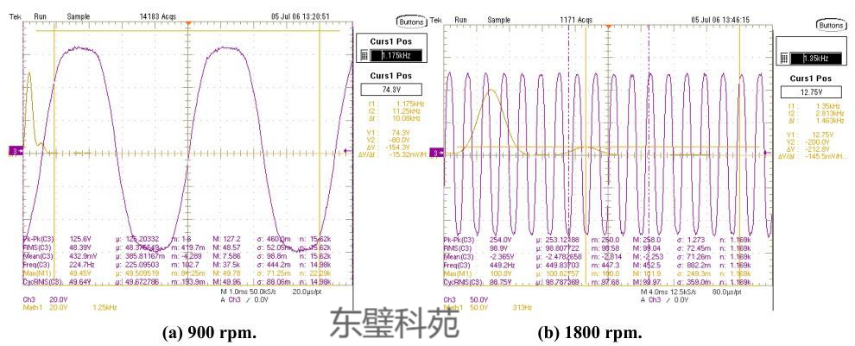
(3)相位变化

高速运行导致BEMF与电流相位差​​增大​​（感性负载相位滞后加剧），而重载会使相位差​​减小；

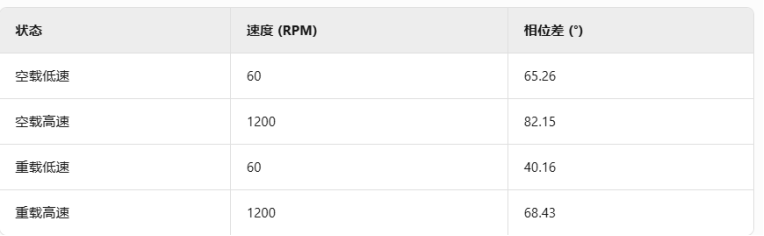
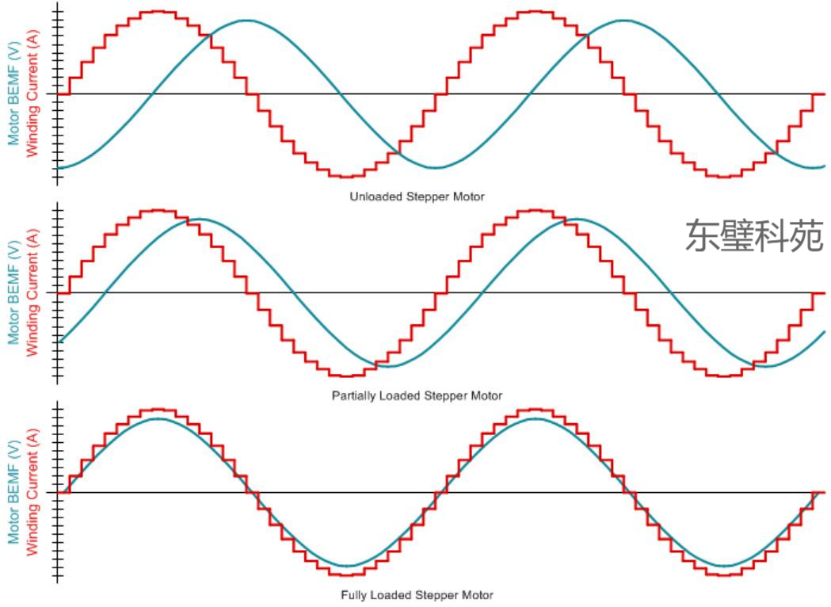
2.反电动势对动态响应的影响

(1) 电流建立延迟，扭矩下降

当电机高速运行时，BEMF可能接近甚至超过母线电压（即驱动器供电电压）。若BEMF ≥ 母线电压，驱动器无法提供足够电压差驱动电流，导致电流下降。当BEMF接近母线电压时，驱动器需100%占空比才能产生正向电流。但实际PWM存在死区时间（Dead Time），导致有效电压仍低于BEMF，电流持续衰减。PWM饱和后，电流控制器无法输出更高电压指令，电流反馈值持续低于目标值，扭矩随之崩溃。

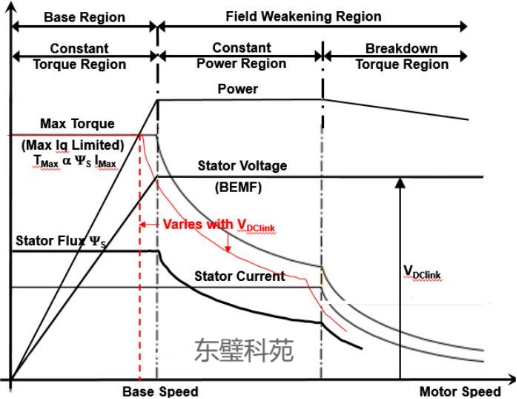
(2) 动态响应滞后

步进电机在高速时，(Vbus​−Ebemf​) 电压裕量减小，导致电流上升率下降，换向延迟，动态响应变慢 。

3.结论

步进电机高速运行时，反电动势幅值增大、频率升高，导致电流建立延迟、扭矩下降及动态响应滞后。所以在步进电机高速运行的方案中，我们需要通过优化电机选型（如低电感、适中极数）、升压驱动及BEMF反馈控制，可缓解高速性能衰减，避免PWM饱和导致的扭矩崩溃。