本次目标
(1)理解并掌握熵Entropy的定义
理解“Huffman”编码是所有编码中总编码长度最短的“熵含义
(2)理解联合熵H(X,Y)、相对熵D(X||Y)、条件熵H(X|Y)、互信息I(X,Y)的定义和含义,并了解如下公式:
a.
H
(
X
∣
Y
)
=
H
(
X
,
Y
)
−
H
(
Y
)
=
H
(
X
)
−
I
(
X
,
Y
)
H(X|Y)=H(X,Y)-H(Y)=H(X)-I(X,Y)
H(X∣Y)=H(X,Y)−H(Y)=H(X)−I(X,Y)
b.
H
(
Y
∣
X
)
=
H
(
X
,
Y
)
−
H
(
X
)
=
H
(
Y
)
−
I
(
X
,
Y
)
H(Y|X)=H(X,Y)-H(X)=H(Y)-I(X,Y)
H(Y∣X)=H(X,Y)−H(X)=H(Y)−I(X,Y)
c.
H
(
X
,
Y
)
=
H
(
X
)
−
H
(
X
∣
Y
)
=
H
(
X
)
+
H
(
Y
)
−
H
(
X
,
Y
)
≥
0
H(X,Y)=H(X)-H(X|Y)=H(X)+H(Y)-H(X,Y)≥0
H(X,Y)=H(X)−H(X∣Y)=H(X)+H(Y)−H(X,Y)≥0
(3)掌握最大熵模型Maxent
(4)了解最大熵模型在自然语言处理NLP中的应用
(5)与前序知识的联系:最大熵模型和极大似然估计MLE的关系
(6)副产品:了解数据分析、函数作图的一般步骤
预备定理:
N
→
∞
⇒
l
n
N
!
→
N
(
l
n
N
−
1
)
N\to∞\Rightarrow lnN!\to N(lnN-1)
N→∞⇒lnN!→N(lnN−1)

再来看一个例子
骰子
(1)普通的一个骰子的某一次投掷,出现点5的概率是多大?
a.等概率:各点的概率都是1/6
b.对于“一无所知”的骰子,假定所有点数等概率出现是“最安全”的做法
(2)对给定的某个骰子,经过N次投掷后发现,点数的均值为5.5,请问:再投一次出现点5的概率有多大?
解:
这是带约束的优化问题
(1)令6个面朝上的概率为
(
p
1
,
p
2
,
.
.
.
,
p
6
)
(p_1,p_2,...,p_6)
(p1,p2,...,p6),用向量
p
p
p表示
(2)目标函数:
H
(
p
^
)
=
−
∑
i
=
1
6
p
i
l
n
p
i
H(\hat{p})=-\sum_{i=1}^6p_ilnp_i
H(p^)=−∑i=16pilnpi
(3)约束条件:
∑
i
=
1
6
p
i
=
1
,
∑
i
=
1
6
i
⋅
p
i
=
5.5
\sum_{i=1}^6p_i=1,\sum_{i=1}^6i\cdot p_i=5.5
∑i=16pi=1,∑i=16i⋅pi=5.5
(4)Lagrange函数:

(5)求解:

预测结果:

可以发现,抛掷一次骰子,出现6的概率其实是最大的
下面渐渐引出熵的概念
从小学数学开始
假设有5个硬币:1,2,3,4,5,其中一个是假的,且比真币轻。有一架没有砝码的天平,天平每次能比较两堆硬币,得出的结果可能是以下三种之一:
a.左边比右边轻;b.右边比左边轻;c.两边同样重
问:至少要几次称量才能确保找到假币?
答案
一种可能的称量方法如下图所示:
答案:2次

但是,为什么称两次就可以呢?
理论下界
a.令
x
x
x表示假硬币的序号:
x
∈
X
{
1
,
2
,
3
,
4
,
5
}
x∈X\lbrace1,2,3,4,5\rbrace
x∈X{1,2,3,4,5}
b.令
y
i
y_i
yi表示第i次使用天平得到的结果:
y
∈
Y
{
1
,
2
,
3
}
y∈Y\lbrace1,2,3\rbrace
y∈Y{1,2,3}
1表示“左轻”,2表示“平衡”,3表示“右轻”
c.用天平称n次,获得的结果是:
y
1
y
2
.
.
.
y
n
y_1y_2...y_n
y1y2...yn;
y
1
y
2
.
.
.
y
n
y_1y_2...y_n
y1y2...yn的所有可能组合数目是
3
n
3^n
3n
d.根据题意,要求通过
y
1
y
2
.
.
.
y
n
y_1y_2...y_n
y1y2...yn确定
x
0
x_0
x0。即影射
m
a
p
(
y
1
y
2
.
.
.
y
n
)
=
x
map(y_1y_2...y_n)=x
map(y1y2...yn)=x
e.从而:
y
1
y
2
.
.
.
y
n
y_1y_2...y_n
y1y2...yn的变化数目大于等于x的变化数目
f.则
3
n
≥
5
3^n≥5
3n≥5,一般意义上:
∣
Y
∣
n
≥
∣
X
∣
|Y|^n≥|X|
∣Y∣n≥∣X∣
进一步分析

a.用
y
1
y
2
.
.
.
y
n
y_1y_2...y_n
y1y2...yn表达x,即设计编码x:
y
1
y
2
.
.
.
y
n
y_1y_2...y_n
y1y2...yn
b.X的“总不确定度”是:
H
(
X
)
=
l
o
g
∣
X
∣
=
l
o
g
5
H(X)=log|X|=log5
H(X)=log∣X∣=log5
c.Y的“表达能力”是:
H
(
Y
)
=
l
o
g
∣
Y
∣
=
l
o
g
3
H(Y)=log|Y|=log3
H(Y)=log∣Y∣=log3
d.至少要多少个Y才能准确表达X?

所以至少要称量2次才能找到假币
题目的变种
(1)假设有5个硬币:1,2,3,4,5,其中一个是假的,比其他的硬币轻。已知第1,2个硬币是假币的概率都是三分之一;第3,4,5个是假硬币的概率都是九分之一
(2)有一架没有砝码的天平,假设使用天平n次能够找到假币,问n的期望值至少是多少?
解:直接用上面的结论做推广:
(1)

(2)思考:我们一直用的
l
o
g
2
p
log_2p
log2p到底是什么东西呢
定义信息量
(1)原则:
a.某事件发生的概率小,则该事件的信息量大
b.如果两个事件X和Y独立,即
p
(
x
y
)
=
p
(
x
)
p
(
y
)
p(xy)=p(x)p(y)
p(xy)=p(x)p(y),假定X和Y的信息量分别为h(X)和h(Y),则二者同时发生的信息量应该为
h
(
X
Y
)
=
h
(
X
)
+
h
(
Y
)
h(XY)=h(X)+h(Y)
h(XY)=h(X)+h(Y)
(2)定义事件X发生的信息量:
h
(
x
)
=
−
l
o
g
2
x
h(x)=-log_2x
h(x)=−log2x
(3)思考:事件X的信息量的期望如何计算呢?
熵
对随机事件的信息量求期望,得熵的定义:

a.注:经典熵的定义,底数是2,单位是bit
b.本例中,为分析方便使用底数e
c.若底数是e,单位是nat(奈特)
研究函数
f
(
x
)
=
x
l
n
x
f(x)=xlnx
f(x)=xlnx
a.
f
(
x
)
=
x
l
n
x
,
x
∈
[
0
,
1
]
f(x)=xlnx,x∈[0,1]
f(x)=xlnx,x∈[0,1]
b.
f
′
(
x
)
=
l
n
x
+
1
f^{'}(x)=lnx+1
f′(x)=lnx+1
c.
f
′
′
(
x
)
=
1
/
x
>
0
(
凸
函
数
)
f^{''}(x)=1/x>0(凸函数)
f′′(x)=1/x>0(凸函数)
d.当
f
′
(
x
)
=
0
时
,
x
=
1
/
e
f^{'}(x)=0时,x=1/e
f′(x)=0时,x=1/e,取极小值
e.由于:

定义
f
(
0
)
=
0
f(0)=0
f(0)=0
对熵的理解:
0
≤
H
(
X
)
≤
l
o
g
∣
X
∣
0≤H(X)≤log|X|
0≤H(X)≤log∣X∣
(1)熵是随机变量不确定性的度量,不确定性越大,熵值越大;若随机变量退化成定值,熵为0
a.该不确定性度量的本质即为信息量的期望
b.均匀分布是“最不确定”的分布
(2)熵其实定义了一个函数(概率分布函数)到一个值(信息熵)的映射
a.
P
(
x
)
→
H
P(x)\to H
P(x)→H(函数
→
\to
→数值)
b.泛函:“变分推导”章节
再来看一下几种典型分布的熵
两点分布的熵
两点分布的熵:


当概率等于0.5时,熵最大,表示最不确定的情况
继续思考:散点分布呢?


组合数的关系
(1)把N件物品分成k组,使得每组物品的个数分别为
n
1
,
n
2
,
.
.
.
,
n
k
,
(
n
=
n
1
+
n
2
+
.
.
.
+
n
k
)
n_1,n_2,...,n_k,(n=n_1+n_2+...+n_k)
n1,n2,...,nk,(n=n1+n2+...+nk),则不同的分组方法有:

记:
求:

公式推导
N
→
∞
⇒
l
n
N
!
→
N
(
l
n
N
−
1
)
N\to∞\Rightarrow lnN!\to N(lnN-1)
N→∞⇒lnN!→N(lnN−1)

思考:根据函数形式判断概率分布
(1)正态分布的概率密度函数
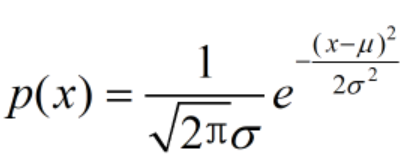
(2)对数正态分布

该分布的对数是关于随机变量x的二次函数
根据计算过程的可逆性,若某对数分布能够写成随机变量二次形式,则该分布必然是正态分布
举例
(1)Gamma分布的意义

(2)对数形式
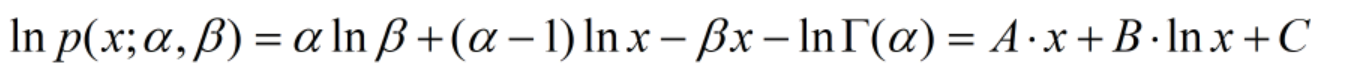
若某对数分布能够写成随机变量一次项和对数项的和,则该分布必然是Gamma分布
(3)注:
a.Gamma函数:

b.Gamma分布的期望为:
E
(
X
)
=
α
β
E(X)=\frac{α}{\beta}
E(X)=βα
最大熵的理解
0
≤
H
(
X
)
≤
l
o
g
∣
X
∣
0≤H(X)≤log|X|
0≤H(X)≤log∣X∣
(1)熵是随机变量不确定性的度量,不确定性越大,熵值越大
a.若随机变量退化成定值,熵最小,为0
b.若随机分布为均匀分布熵最大
(2)以上是无条件的最大熵分布,若有条件呢?
最大熵模型
(3)思考:只给定期望和方差的前提下,最大熵的分布形式是什么?
思考过程
(1)建立目标函数

(2)使用方差公式化简约束条件

(3)显然,此问题为带约束的极值问题
Lagrange乘子法
建立Lagrange函数,求驻点

P
(
x
)
P(x)
P(x)的对数是关于随机变量x的二次形式,所以该分布p(x)必然是正态分布!
联合熵和条件熵
(1)两个随机变量X,Y的联合分布,可以形成联合熵Joint Entropy,用H(X,Y)表示
(2)H(X,Y)-H(Y)
a.(X,Y)发生所包含的熵,减去Y单独发生包含的熵:在Y发生的前提下,X发生“新”带来的熵
b.该式子定义为Y发生前提下,X的熵:
条件熵H(X|Y)
推导条件熵的定义式

根据条件熵的定义式,可以得到:

相对熵
(1)相对熵,又称互熵,交叉熵,鉴别信息,Kullback熵,Kullback-Leible散度等
(2)设p(x),q(x)是X中取值的两个概率分布,则p对q的相对熵是:

(3)说明:
a.相对熵可以度量两个随机变量的“距离”
b.一般的,D(p||q)≠D(q||p)
c.D(p||q)≥0、D(q||p)≥0;凸函数中的Jensen不等式
思考
(1)假定已知随机变量P,求相对简单的随机变量Q,使得Q尽量接近P
a.方法:使用P和Q的K-L距离
b.难点:K-L距离是非对称的,两个随机变量应该谁在前谁在后呢?
(2)假定使用KL(Q||P),为了让距离最小,则要求在P为0的地方,Q尽量为0,会得到比较“窄”的分布曲线;
(3)假定使用KL(P||Q),为了让距离最小,则要求在P不为0的地方,Q也尽量不为0.会得到比较“宽”的分布曲线
两个KL散度的区别
绿色曲线是真实分布p的等高线;红色曲线是使用近似
p
(
z
1
,
z
2
)
=
p
(
z
1
)
p
(
z
2
)
p(z_1,z_2)=p(z_1)p(z_2)
p(z1,z2)=p(z1)p(z2)得到的等高线
a.左:
K
L
(
p
∣
∣
q
)
:
z
e
r
o
a
v
o
i
d
i
n
g
KL(p||q):zero avoiding
KL(p∣∣q):zeroavoiding
b.右:
K
L
(
q
∣
∣
p
)
:
z
e
r
o
f
o
r
c
i
n
g
KL(q||p):zero forcing
KL(q∣∣p):zeroforcing

互信息
(1)两个随机变量X,Y的互信息,定义为X,Y的联合分布和独立分布乘积的相对熵
(2)
I
(
X
,
Y
)
=
D
(
P
(
X
,
Y
)
∣
∣
P
(
X
)
P
(
Y
)
I(X,Y)=D(P(X,Y)||P(X)P(Y)
I(X,Y)=D(P(X,Y)∣∣P(X)P(Y)

计算条件熵的定义式:
H
(
X
)
−
I
(
X
,
Y
)
H(X)-I(X,Y)
H(X)−I(X,Y)

整理得到的等式
(1)
H
(
X
∣
Y
)
=
H
(
X
,
Y
)
−
H
(
Y
)
H(X|Y)=H(X,Y)-H(Y)
H(X∣Y)=H(X,Y)−H(Y)条件熵定义
(2)
H
(
X
,
Y
)
=
H
(
X
)
−
I
(
X
,
Y
)
H(X,Y)=H(X)-I(X,Y)
H(X,Y)=H(X)−I(X,Y)根据信息定义展开得到
(3)对偶式
H
(
Y
∣
X
)
=
H
(
X
,
Y
)
−
H
(
X
)
H(Y|X)=H(X,Y)-H(X)
H(Y∣X)=H(X,Y)−H(X)
H
(
Y
∣
X
)
=
H
(
Y
)
−
I
(
X
,
Y
)
H(Y|X)=H(Y)-I(X,Y)
H(Y∣X)=H(Y)−I(X,Y)
(4)
I
(
X
,
Y
)
=
H
(
X
)
+
H
(
Y
)
−
H
(
X
,
Y
)
I(X,Y)=H(X)+H(Y)-H(X,Y)
I(X,Y)=H(X)+H(Y)−H(X,Y)
有些文献将该式作为互信息的定义式
(5)试证明:
H
(
X
∣
Y
)
≤
H
(
X
)
,
H
(
Y
∣
X
)
≤
H
(
Y
)
H(X|Y)≤H(X),H(Y|X)≤H(Y)
H(X∣Y)≤H(X),H(Y∣X)≤H(Y)
强大的维恩图帮助记忆

最大熵模型的原则
a.承认已知事物(知识)
b.对未知事物不做任何假设,没有任何偏见
引入新知识
(1)若已知:“学习”被标为定语的可能性很小,只有0.05,
p
(
y
4
)
=
0.05
p(y_4)=0.05
p(y4)=0.05
(2)仍然坚持无偏原则:
p
(
x
1
)
=
p
(
x
2
)
=
0.5
p(x_1)=p(x_2)=0.5
p(x1)=p(x2)=0.5
p
(
y
1
)
=
p
(
y
2
)
=
p
(
y
3
)
=
0.95
/
3
p(y_1)=p(y_2)=p(y_3)=0.95/3
p(y1)=p(y2)=p(y3)=0.95/3
再次引入新知识
(1)当“学习”被标作动词的时候,它被标作谓语的概率为0.95
p
(
y
2
∣
x
1
)
=
0.95
p(y_2|x_1)=0.95
p(y2∣x1)=0.95
(2)除此之外,仍然坚持无偏原则, 尽量使概率平均分布
(3)问:怎么样能尽量无偏分布?
最大熵模型Maximum Entropy
(1)概率平均分布等价于熵最大
(2)问题转化为:计算X和Y的分布,使H(Y|X)达到最大值,并且满足条件
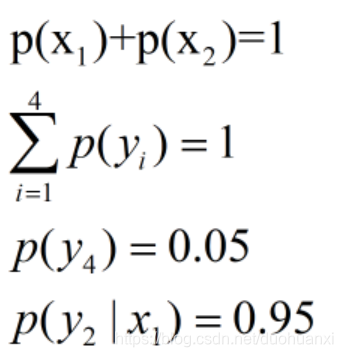
特征函数
(1)关于某个特征(x,y)的样本
a.y:这个特征中需要确定的信息
b.x:这个特征中的上下文信息
(2)特征函数:对于一个特征
(
x
0
,
y
0
)
(x_0,y_0)
(x0,y0),定义特征函数:

(3)对于一个特征
(
x
0
,
y
0
)
(x_0,y_0)
(x0,y0),在样本中的期望值是:

p
‾
\overline{p}
p是(x,y)在样本中出现的概率
条件Constraints
(1)对每一个特征(x,y),模型所建立的条件概率分布要与训练样本表现出来的分布相同
(2)假设样本的分布(已知):

特征f在模型中的期望值:

最大熵模型总结
(1)定义条件熵:

(2)模型目的:

(3)定义特征函数:

(4)约束条件:

ok,这篇文章暂且到这里吧

























 4886
4886

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








