通用算法 - [图算法] - 拓扑排序

1、什么是拓扑排序？

在一个有向图中，我们对顶点进行排序，使得排序后的顶点序列满足：如果顶点$V_i$和$V_j$存在一条有向边$<V_i，V_j>$，那么在该序列中，顶点$V_j$一定在顶点$V_i$的后面。
注意，该有向图一定是有向无环图，否则不存在拓扑序列。

例如在下面这个有向图中，$<a，c，b，f，d，e>$就是该有向图的一个拓扑序列

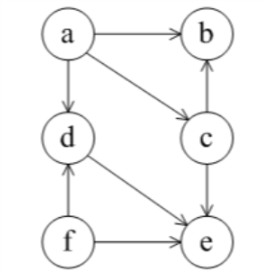
2、拓扑排序的应用场景

在实际应用中，有向图中的边可以看成是顶点之间依赖关系的描述。把顶点看成是一个个的任务，那么有向边$<V_i，V_j>$表示的是任务$V_j$依赖于任务$V_i$，任务$V_i$必须先于任务$V_j$完成。
所以，拓扑排序实际上是用来排序具有依赖关系的任务。

应用场景1：大学要修N门课程，这N门课程中有些课程存在依赖关系，比如算法这门课依赖于数据结构，问如何安排这N门课程才比较合理？

应用场景2：一个机器要完成N个任务，有些任务之间存在依赖关系，问如何安排这N个任务才能使最终完成时间最短？

应用场景3：给N个人分配N个任务，每个人完成这N个任务的花费代价已知，部分任务之间存在依赖关系，问如何安排才能使得最终的代价最小。

应用场景4：给定由26个小写字母组成的字符串和一些字母间的偏序关系，输出满足所有偏序关系的字符串。

3、单个拓扑序列的生成算法

单个拓扑序列生成是指只要找到有向图的一个拓扑序列即可。
单个拓扑序列生成算法思想：
（1）根据偏序关系（有向边）构建有向图；
（2）从有向图中一个入度为0的顶点$V_i$，并输出；
（3）将$V_i$指向顶点的入度减去1；
（4）重复步骤(2)、（3），直到所有顶点都输出或有向图中不存在入度为0的顶点为止。

下面是根据该算法思想生成有向图的拓扑序列一个例子：

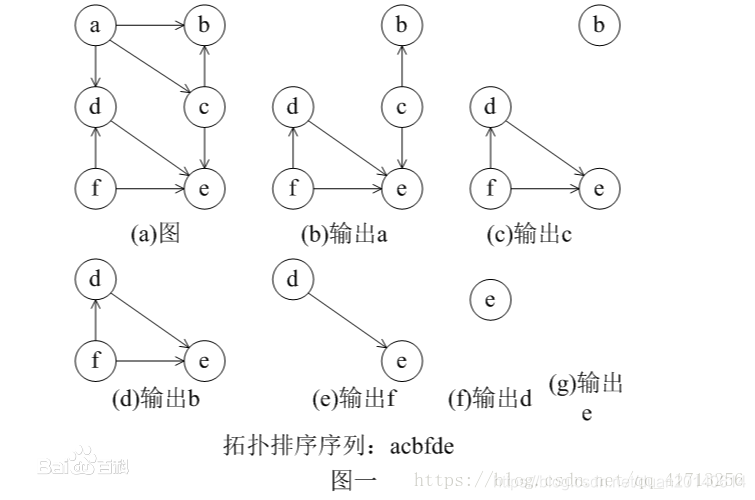
在使用程序实现时，可能需要特别考虑的是数据结构的设计问题：
（1）有向图的存储
有向图可以采用邻接矩阵或邻接表来储存，但在一般情况下，有向图是一个稀疏矩阵，所以采用邻接表来存储比较合理，邻接表是一个二维的矩阵，行数为顶点的个数，列数不确定，主要取决于顶点的边数，例如$edge[i][j]$存储的是第$i$个顶点第$j$条边所指向的顶点。
（2）每个顶点入度的存储：
使用一个数组或哈希表$invertex$来记录每个顶点的入度，$invertex[i]$表示顶点$V_i$的入度。
（3）每个入度为0的顶点的访问情况：
这个有两种表示方法：

• 方法1：使用数组或哈希表$visit$记录每个顶点的访问情况，如果节点$V_i$被访问过，则$visit[i]$被设置成False；
• 方法2：使用队列$queue$来表示，如果顶点是已经访问过的，则从队列中删除，如果是将要被访问的，则添加到队列中。
• 区别：这两种方法各有优缺点，方法1能很明晰的知道哪些节点被访问过，哪些节点是没有被访问过，这在回溯法中特别重要，因为利用回溯法的过程中，当某个顶点的边全部被访问过之后，需要回溯，即将该顶点标为重新标记为未访问；方法2适用于不需要记录访问过的顶点的时候。如果要求输出的拓扑序列是按照字典序的时候，只需要将队列改成优先队列（堆）即可。

如果求有向图的单个拓扑序列，则一般采用$edge$、$invertex$、以及$queue$等三种数据结构。
具体实现程序如下：

def SingleTopoSeq(edge,invertex):

    toposeq = []

    vertex_nums = len(invertex)

    queue = []

    for v in range(0,vertex_nums):

        if invertex[v] == 0:

            queue.append(v)
            
    while len(queue) != 0:

        vertex = queue[0]

        toposeq.append(vertex)

        queue.remove(vertex)

        for e_ind in range(0,len(edge[vertex])):

            vertex_pointed = edge[vertex][e_ind]

            invertex[vertex_pointed] -= 1

            if invertex[vertex_pointed] == 0:
                
                queue.append(vertex_pointed)


    return toposeq
	

4、全部拓扑序列的生成算法

若要生成全部的拓扑序列，则需要使用$edege$、$invertex$以及$visit$结合回溯法求解。
具体实现程序如下所示：

class AllTopoSeq:

    toposeq = []

    invertex = None

    edge = None

    visit = None

    alltoposeqs = []


    def Find(self, edge, invertex):

        self.invertex = invertex

        self.edge = edge

        self.visit = [False] * len(invertex)

        self.DFS(0)

        return self.alltoposeqs


    def DFS(self,layer):

        if len(self.toposeq) == len(self.visit):

            #注意，需要重新拷贝一份toposeq,
            #如果直接alltoposeq.append(toposeq),
            #则在toposeq发生变化的时候，alltoposeqs中的内容也会发生变化。

            toposeq_copy = list(self.toposeq)

            self.alltoposeqs.append(toposeq_copy)
            
            return 

        for v in range(0,len(self.visit)):

            if self.invertex[v] == 0 and self.visit[v] == False:

                self.toposeq.append(v) 

                self.visit[v] = True

                for e_ind in range(0,len(edge[v])):

                    vertex_pointed = edge[v][e_ind]

                    self.invertex[vertex_pointed] -= 1
                    

                self.DFS(layer + 1)
                

                for e_ind in range(0,len(edge[v])):

                    vertex_pointed = edge[v][e_ind]

                    self.invertex[vertex_pointed] += 1

                self.visit[v] = False

                self.toposeq.pop()
        
        return

5、应用实例

问题描述：

多多鸡在公司负责一个分布式任务执行平台的维护。夏天到了，平台的服务器都因中暑而无法执行任务了。所以多多鸡必须自己手动来执行每个任务!
现在一共有N个待执行的任务，每个任务多多鸡需要P1的时间完成执行。同时，任务之间可能会有一些依赖关系。比如任务1可能依赖任务2和任务3，那么任务1必须在任务2和任务3都执行完成后才能执行。
多多鸡只有一个人，所以同时只能执行一个任务，并且在任务完成之前不能暂停切换去执行其他任务。 为了提升平台用户的使用体验，多多鸡希望最小化任务的平均返回时长。一个任务的返回时长定义为任务执行完成时刻减去平台接收到该任务的时刻。在零时间，所有N个任务都已经被平台接收。请你帮多多鸡安排下任务执行顺序，使得平均返回时长最
小。
输入描述:
第一行包含2个正整数N、M，分别表示任务数量以及M个任务依赖关系。
第二行包含N个正整数，第i(1<=1<=N)个数表示第i个任务的处理时间Pi。
接下来的M行，每行表示一个任务依赖关系。每行包含2个整数Ai(1<=Ai<=N)、B1(1<=Bi<=N)，表示第B1个任务依赖于第A1个任务。数据保证不会出现循环依赖的情况。数据范围:
1<=N<=1000

1<=M<=50000

1<=P1<=10000
输出描述:
输出一行，包含N个整数(两两之间用一个空格符分隔)，其中第i(1<=i<=N)个整数表示多多鸡执行的第i个任务的编号。若有多种可行方案,则输出字典序最小(优先执行编号轮小的任务的方案。

例：

输入：

5 6

1 2 1 1 1

1 2

1 3

1 4

2 5

3 5

4 5

输出：

1 3 4 2 5 （输出的是执行顺序）；

解题思路：

• 这是拓扑排序的典型应用，和应用场景2属于同一类型题，需要注意的概念是平均返回时长，一个任务的返回时长是指任务完成时刻减去平台接收该任务的时刻。
• 以上述例子解释一下，假设任务的执行顺序是1、3、4、2、5，任务1的完成时刻是1，到达时刻是0，所以返回时长是1-0 = 1，任务3的完成时刻是任务1的执行时长加上任务3的执行时长1+1=2，到达时刻是0，所以返回时长是2-0=2，以此类推，任务4的返回时长是1+1+1-0=3，任务2的返回时长是1+1+1+2-0=5，任务5的返回时长是1+1+1+2+1-0=6。

6、回溯法生成序列的全排代码模板

实际上，有向图全部拓扑序列的生成算法实际是使用回溯法生成序列全排列的变形，使用回溯法生成序列的全排列的算法模板如下所示：

#使用回溯法生成全排列
def permutation(seq_org):

    visit = [False] * len(seq_org)

    seq_per = []

    results = []

    DFS(0,seq_org,visit,seq_per,results)

    print("result={}".format(results))

    
    
def DFS(layer,seq_org,visit,seq_per,results):

    if len(seq_per) == len(visit):

        results.append(list(seq_per))

        return

    for i in range(0,len(visit)):

        if visit[i] == False:

            seq_per.append(seq_org[i])

			print('seq_per={}’.format(seq_per))

            visit[i] = True

            DFS(layer + 1,seq_org,visit,seq_per,results)

            visit[i] = False

            seq_per.pop()

    return 

if __name__ == '__main__':

    seq = ['x','y','z']
    
    permutation(seq) 
    

输出结果

seq_per=['x']
seq_per=['x', 'y']
seq_per=['x', 'y', 'z']
seq_per=['x', 'z']
seq_per=['x', 'z', 'y']
seq_per=['y']
seq_per=['y', 'x']
seq_per=['y', 'x', 'z']
seq_per=['y', 'z']
seq_per=['y', 'z', 'x']
seq_per=['z']
seq_per=['z', 'x']
seq_per=['z', 'x', 'y']
seq_per=['z', 'y']
seq_per=['z', 'y', 'x']
results=[['x', 'y', 'z'], ['x', 'z', 'y'], ['y', 'x', 'z'], ['y', 'z', 'x'], ['z', 'x', 'y'], ['z', 'y', 'x']]

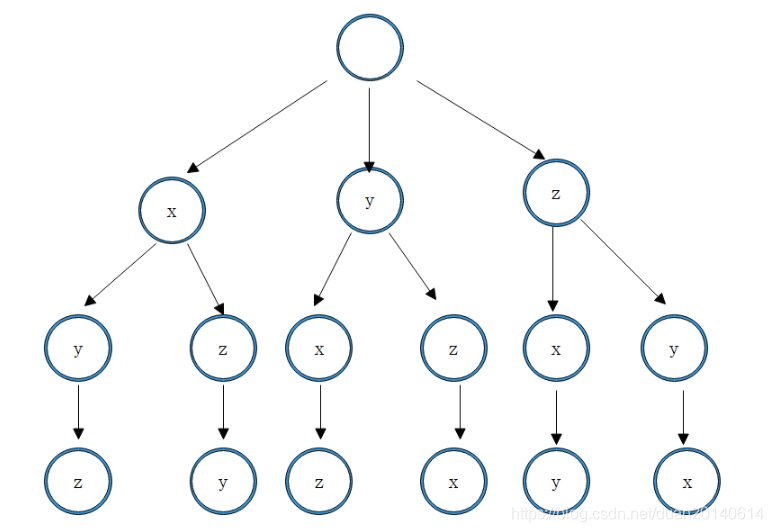
结合上图和输出结果可以看出，seq_per实际上存储的是排列树上的各个节点的访问顺序。