上一篇文章中我们直观的感受了当θ0=0\theta_{0}=0θ0=0时,代价函数的J(θ)J(\theta)J(θ)几何图像。
接下来,看看当θ0!=0\theta_{0}!=0θ0!=0时,其几何图形会是什么样的呢?
首先,让我们先来了解以下什么是轮廓图。
假设J(θ0,θ1)J(\theta_{0},\theta_{1})J(θ0,θ1)实际的图形如下所示:
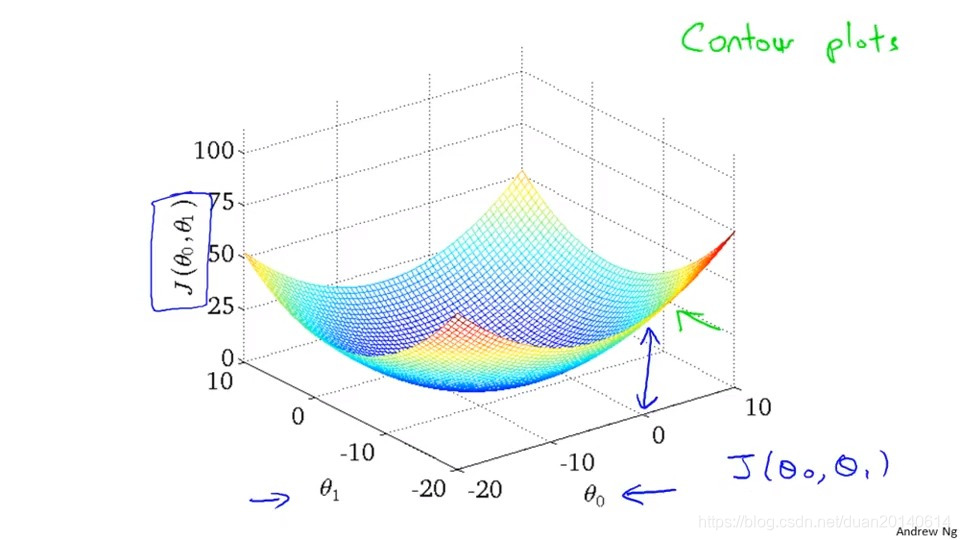
则等值线图是将该曲面投影到(θ0,θ1)(\theta_{0},\theta_{1})(θ0,θ1)平面上所形成的图形,等值线图包含许多等值线,同一等值线上函数值相同,但是所对应θ0\theta_{0}θ0和θ1\theta_{1}θ1却不一定相同,比如下面右边的图中的三个绿色点。
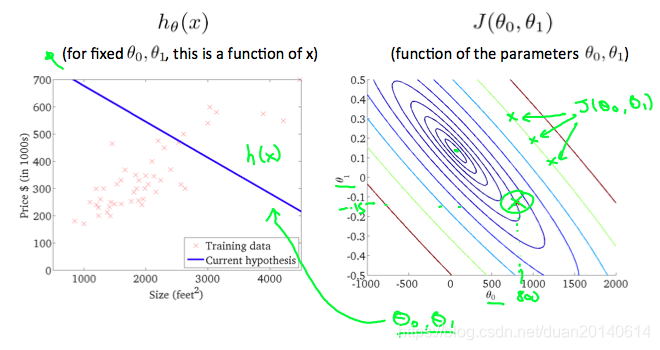
(1). 当(θ0=360,θ1=0)(\theta_{0}=360,\theta_{1}=0)(θ0=360,θ1=0)时
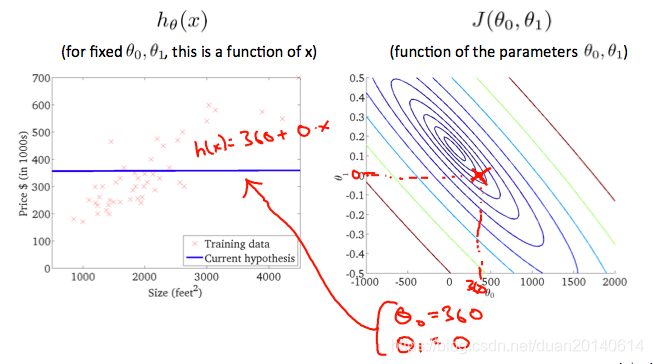
(2). 当(θ0=250,θ1=0.12)(\theta_{0}=250,\theta_{1}=0.12)(θ0=250,θ1=0.12)时:
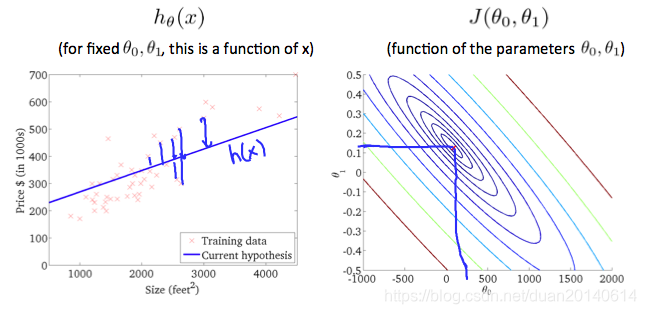
- 从以上几幅图中可以看出,随着(θ0,θ1)(\theta_{0},\theta_{1})(θ0,θ1)越靠近等值线图的中心,代价函数J(θ0,θ1)J(\theta_{0},\theta_{1})J(θ0,θ1)的值越小,假设函数hθh_{\theta}hθ也更加的拟合样本点





 文章承接上文,探讨当θ0≠0时代价函数J(θ)的几何图形。先介绍了轮廓图,即J(θ0,θ1)曲面投影到(θ0,θ1)平面形成的等值线图,同一等值线上函数值相同但θ0和θ1不一定相同。还指出(θ0,θ1)越靠近等值线图中心,代价函数值越小,假设函数更拟合样本点。
文章承接上文,探讨当θ0≠0时代价函数J(θ)的几何图形。先介绍了轮廓图,即J(θ0,θ1)曲面投影到(θ0,θ1)平面形成的等值线图,同一等值线上函数值相同但θ0和θ1不一定相同。还指出(θ0,θ1)越靠近等值线图中心,代价函数值越小,假设函数更拟合样本点。

















 1606
1606

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










