上篇文章中我们提到了代价函数J(θ)J(\theta)J(θ),并期望使它最小化,那代价函数长什么样子呢?
接下来,我们将给大家一个直观的感受,看看参数θ\thetaθ取不同值时,J(θ)J(\theta)J(θ)的几何呈现
我们可以把训练集中的样本(x,y)(x,y)(x,y)想象成分散在xy平面上的点,然后通过一条直线来拟合这些点,这条直线就是我们的假设函数hθ(x)=θ0+θ1xh_{\theta}(x)=\theta_{0}+\theta_{1}xhθ(x)=θ0+θ1x,这里我们令θ0=0\theta_{0}=0θ0=0,看J(θ)J(\theta)J(θ)随θ1\theta_{1}θ1的变化情况
(1). 当θ1=1时\theta_{1}=1时θ1=1时,hθh_{\theta}hθ和J(θ)J(\theta)J(θ)的几何意义分别如下:
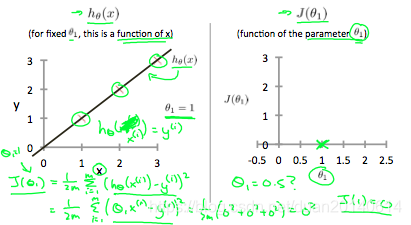
从上图右可以看出,当θ1=1时\theta_{1}=1时θ1=1时,代价函数的值(绿叉表示的点)J(θ)=0J(\theta)=0J(θ)=0
(2). 当θ1=0.5时\theta_{1}=0.5时θ1=0.5时,hθh_{\theta}hθ和J(θ)J(\theta)J(θ)的几何意义分别如下:
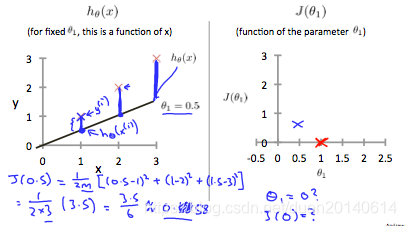
从上图右可以看出,当θ1=0.5\theta_{1}=0.5θ1=0.5时,代价函数的值(蓝叉表示的点)J(θ)=0.58J(\theta)=0.58J(θ)=0.58,增加了0.58。
(3). 我们把θ1\theta_{1}θ1一些可能的取值画出来,就形成了以下曲线:
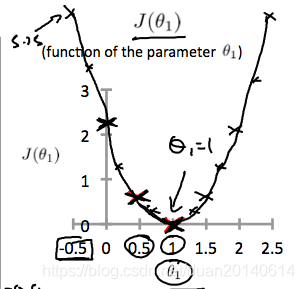





 文章围绕代价函数J(θ)展开,期望使其最小化。通过将训练集样本想象成xy平面上的点,用假设函数hθ(x)=θ0+θ1x拟合,令θ0=0,展示了θ1取不同值(如1、0.5)时,代价函数J(θ)的几何意义及数值变化,还提到将θ1取值绘成曲线。
文章围绕代价函数J(θ)展开,期望使其最小化。通过将训练集样本想象成xy平面上的点,用假设函数hθ(x)=θ0+θ1x拟合,令θ0=0,展示了θ1取不同值(如1、0.5)时,代价函数J(θ)的几何意义及数值变化,还提到将θ1取值绘成曲线。

















 302
302

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










