本文介绍了不同类型的树结构，包括二叉树的各种形式如满二叉树、完全二叉树、哈夫曼树等，以及多路搜索树如B树、B+树，并详细解析了红黑树的特性和约束条件。
结点的度：一个结点含有子树的个数。
数的度：最大结点的度成为树的度。
1、满二叉树：除最后一层子结点外，每一层上的结点都有两个结点。
2、完全二叉树：除最后两层子结点外，每一层上的结点都有两个结点，最后一层的结点都几种在连续的最左边。
3、最优二叉树（哈夫曼树）：具有最小带权路径长度的二叉树。
4、二叉排序树（二叉搜寻树）（二叉查找树BST）：二叉排序树是按中序已经排序好的数据。
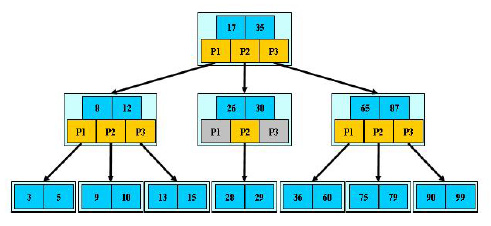
5、B树（B-树）：多路搜索树
关键字集中分布在整棵树中，任何一个关键字出现且只出现在一个结点中，搜索有可能在非叶子结点结束。
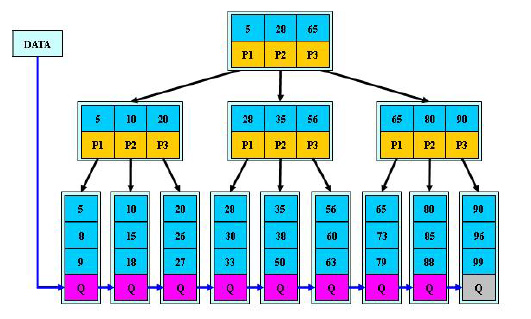
6、B+树：
B+树中的所有叶子节点包含了所有关键字的信息，所有关键字都在叶子节点出现。
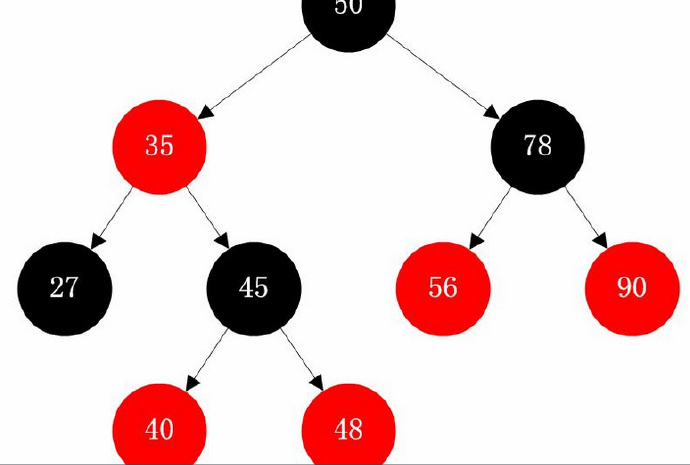
7、红黑树：
红黑树是一种自平衡二叉查找树，是每个节点都带有颜色属性的二叉查找树，颜色为黑色和红色。约束：性质1. 节点是红色或黑色。
性质2. 根节点是黑色。
性质3 每个叶节点（NIL节点，空节点）是黑色的。
性质4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
性质5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
这些约束强制了红黑树的关键性质: 从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例，这个在高度上的理论上限允许红黑树在最坏情况下都是高效的，而不同于普通的二叉查找树。
扫一扫
2671
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
