“蔚来杯“2022牛客暑期多校训练营5-F-A Stack of CDs

本文详细介绍了如何通过数学方法解决牛客网'蔚来杯'2022暑期多校训练营中关于圆盘轮廓周长的问题，涉及圆心角计算、圆盘覆盖分析和算法实现，适合对ACM竞赛感兴趣的学生和开发者阅读。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

"蔚来杯"2022牛客暑期多校训练营5-F-A Stack of CDs

题目大意

链接：https://ac.nowcoder.com/acm/contest/33190/F
来源：牛客网
有 $n$ 个圆盘,它们堆在一个二维平面上,彼此之间可能会覆盖对方,求从上往下看能看到的圆盘轮廓周长。
输入的顺序代表了圆盘从下到上的顺序。

解析

这道题可以说就是一道数学题,做法很多,我的思路如下:

对于一个圆盘 $a_i$ ,只需要看编号大于 $i$ 的圆盘有没有将其覆盖。
以水平向右为始边,逆时针方向为正方向,角度均用弧度制。
将圆盘 $a_i$ 被覆盖的弧对应的圆心角的左右边界记录下来,并且在最后把有交集的区间合并。
答案即为所有圆盘的周长减去每个圆盘被覆盖的弧长。

唯一的难点在于求被覆盖圆弧对应的圆心角。对于圆 $a$ 和圆 $b$ ( $b$ 在 $a$ 上方),我们要考虑他们的四种关系(两圆圆心相距 $d$ ,即 $∣ A B ∣ = d$ )。

相交:

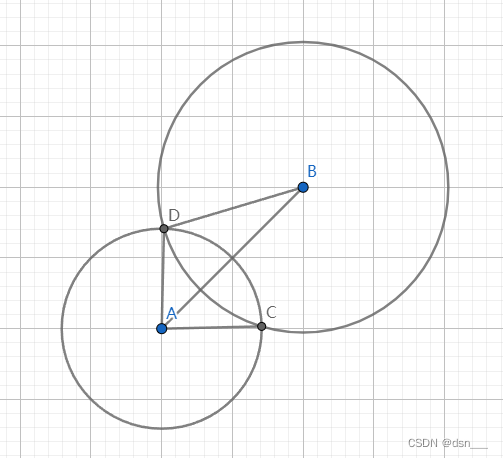
如图所示,可用余弦定理求出 $cos⁡θ=(ra2+d2−rb2)/(2×d×ra)\cos \theta = (r_a^2 + d^2 - r_b^2)/(2\times d\times r_a)$ ,从而求出 $θ(∠BAD)\theta(\angle BAD)$ 。
为了使所有角的区间在 $[0,2×π][0,2\times \pi]$ 之间,有时要将一个区间拆成两个,具体见代码。
相离
没有覆盖,直接跳过。
此时 $ra+rb≥dr_a + r_b \ge d$
$a$ 包含 $b$
$b$ 没有覆盖 $a$ ,也直接跳过。
此时 $rb+d≤rar_b +d \le r_a$
$b$ 包含 $a$
$a$ 被 $b$ 完全覆盖,直接在 $a$ 被覆盖的角的区间加入 $\times \pi]$
此时 $ra+d≤rbr_a + d \le r_b$

参考代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<vector>
#include<math.h>
#include<string.h>

using namespace std;

typedef long long ll;

struct node{
	double l,r;
};

struct circle{
	ll x,y,r;
}c[1010];

const double pi = acos( -1.0 );

double dis(circle a,circle b){
	return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}

bool cmp(node a,node b){
	return a.l < b.l;
}

node angle[1100][2010];
int n,cnt[1100];

int main(){
	while(~scanf("%d",&n)){
		node em;
		em.l = 0.0;
		em.r = 0.0;
		memset(cnt,0,sizeof(cnt));
		for(int i=0;i<=n;i++){
			for(int j=0;j<=n;j++){
				angle[i][j] = em;
			}
		}
		for(int i=1;i<=n;i++){
			scanf("%lld%lld%lld",&c[i].x,&c[i].y,&c[i].r);
		}
		for(int i=1;i<=n;i++){
			for(int j=i + 1;j<=n;j++){
				double d = dis(c[i],c[j]),r1 = 1.0 * c[i].r,r2 = 1.0 * c[j].r;
				if(d >= r1 + r2 ) continue;
				if(r2 >= r1 + d ){
					node x;
					x.l = 0.0;
					x.r = 2.0 * pi;
					angle[i][++cnt[i]] = x;
					continue;
				}
				if (r1 >= r2 + d){
					continue;
				}
				double a = atan2(c[j].y - c[i].y , c[j].x - c[i].x);
				double a1 = acos((r1 * r1 + d * d - r2 * r2) / (2.0 * r1 * d));
				if(a < 0.0) a = a + 2.0 * pi;
				node a2,tmp;
				a2.l = a - a1;
				a2.r = a + a1;
				if(a2.l < 0.0){
					tmp.l = a2.l + 2.0 * pi;
					tmp.r = 2.0 * pi;
					a2.l = 0.0;
					angle[i][++cnt[i]] = tmp;
				}
				if(a2.r > 2.0 * pi){
					tmp.l = 0.0;
					tmp.r = a2.r - 2.0 * pi;
					a2.r = 2.0 * pi;
					angle[i][++cnt[i]] = tmp;
				}
				angle[i][++cnt[i]] = a2;
			}
		}
		double ans = 0.0;
		for(int i=1;i<=n;i++){
			ans += c[i].r * 2.0 * pi;
			int tcnt = 0;
			if(!cnt[i])continue;
			sort(angle[i] + 1,angle[i] + cnt[i] + 1,cmp);
			for(int j=2;j<=cnt[i];j++){
				if(angle[i][j].l <= angle[i][j - 1].r){
					angle[i][j].l = angle[i][j - 1].l;
					angle[i][j].r = max(angle[i][j - 1].r , angle[i][j].r);
				}
				else angle[i][tcnt++] = angle[i][j - 1];
			}
			angle[i][tcnt++] = angle[i][cnt[i]];
			for(int j=0;j<tcnt;j++){
				ans -= 1.0 * c[i].r * (angle[i][j].r - angle[i][j].l);
			}
		}
		printf("%.12f\n",ans);
	}
}