“蔚来杯“2022牛客暑期多校训练营6-M-Z-Game on grid_alice 和 bob 正在棋盘上玩游戏。-优快云博客

本文链接：https://blog.youkuaiyun.com/dsn___/article/details/126210406

这篇博客探讨了一种两人棋盘游戏的策略，玩家Alice和Bob在n×m的棋盘上移动，目标是到达'A'、'B'或棋盘边缘。通过位运算和动态规划，分析了在不同情况下Alice和Bob的获胜策略，以及如何确保特定的获胜条件。文章提供了一个C++代码示例来解决这个问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

"蔚来杯"2022牛客暑期多校训练营6-M-Z-Game on grid

题目大意

Alice和Bob在一个 $n×mn\times m$ 的棋盘上玩游戏,起点为 $(0, 0)$ ,每次只能向下移一格或向右移一格,即从 $(x, y)$ 移至 $(x + 1, y)$ 或 $(x, y + 1)$ 。棋盘上有’A’和’B’,移动至’A’为Alice赢,移动至’B’为Bob赢,移动至 $(n, m)$ 为平局。现在,Alice先移动,问有没有走法使Bob无论怎么走,结果都为Alice赢或平局或Bob赢。

解析

这是一道博弈题,所以我们先把问题拆分成小一点的情况来分析(黄色框表示当前所在格子)。

1

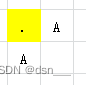
显然,此时不管怎么走,都是Alice赢,都为B也是同理,为Bob赢。
2

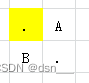
此时的结果就与走的人有关了,如果此时Alice走,那么Alice可以保证Alice赢或是Bob赢,而如果此时是Bob走,那么Alice就不能保证输赢。因为每次只能走一格,我们可以得到,当位于 $(x, y)$ 时,若 $(x + y) m o d 2 = 0$ 说明下一步是Alice走,否则为Bob走。
3
当位于边界时,此时只有一个方向可走,所以当前的胜利状态与下一步的状态相同。

我们可以用二进制数来表示当前格点的胜利状态,第一位为 $1$ 表示位于该节点是Alice能保证Alice能赢,同理第二位表示平局,第三位表示Bob能赢。用dp数组存储,用位运算更新。
用dfs进行记忆化搜索,此时便可省略状态1。若此时为Alice走, $dp_{x,y}=dp_{x+1,y}|dp_{x,y+1}$ ( $∣$ 表示位或)因为当Alice走时,她走不同的点就能保证对应点的胜利状态);若此时为Bob走, $dp_{x,y} =dp_{x+1,y} \& dp_{x,y+1}$ ( $&\&$ 表示位于)因为当Bob走时只有两点胜利状态相同的部分才能留下。答案看 $dp_{0,0}$ 。

参考代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<string.h>
#include<math.h>
#include<queue>
#include<set>
#include<map>
#include<stack>
#include<vector> 

using namespace std;

typedef long long ll;

int t,n,m,dp[510][510];
char mapp[510][510];

int dfs(int x,int y){
	if(dp[x][y] != -1) return dp[x][y];
	if(mapp[x][y] == 'A') return dp[x][y] = 1;
	if(mapp[x][y] == 'B') return dp[x][y] = 1 << 2;
	if(x == n - 1 && y == m - 1) return dp[x][y] = 1 << 1;
	if(x == n - 1) return dp[x][y] = dfs(x,y + 1);
	if(y == m - 1) return dp[x][y] = dfs(x + 1,y);
	if((x + y) % 2 == 0) return dp[x][y] = dfs(x + 1,y) | dfs(x,y + 1);
	else return dp[x][y] = dfs(x + 1,y) & dfs(x,y + 1);
}

int main(){
	scanf("%d",&t);
	while(t--){
		scanf("%d%d",&n,&m);
		memset(dp,-1,sizeof(dp));
		for(int i=0;i<n;i++) scanf(" %s",&mapp[i]);
		int ans = dfs(0,0);
		if(ans & 1) printf("yes ");
		else printf("no ");
		if(ans & (1 << 1)) printf("yes ");
		else printf("no ");
		if(ans & (1 << 2)) printf("yes\n");
		else printf("no\n");
	}
}