机器学习方法原理及编程实现--03.朴素贝叶斯分类器(实现MNIST数据分类)

最新推荐文章于 2025-03-18 11:56:15 发布

drilistbox

最新推荐文章于 2025-03-18 11:56:15 发布

阅读量3.4k

点赞数

分类专栏：机器学习

本文链接：https://blog.youkuaiyun.com/drilistbox/article/details/79788643

版权

机器学习专栏收录该内容

8 篇文章

订阅专栏

文章列表
1.[机器学习方法原理及编程实现–01.K近邻法(实现MNIST数据分类)][1].
2.[机器学习方法原理及编程实现–01.][2].
3.[机器学习方法原理及编程实现–03.朴素贝叶斯分类器(实现MNIST数据分类) ][3].
4.[机器学习方法原理及编程实现–01. ][4].
5.[机器学习方法原理及编程实现–01.][5].
6.[机器学习方法原理及编程实现–01.][6].
[1]: http://blog.youkuaiyun.com/drilistbox/article/details/79341381
[2]: http://blog.youkuaiyun.com/drilistbox/article/details/79342784
[3]: http://blog.youkuaiyun.com/drilistbox/article/details/79345703
[4]: http://blog.youkuaiyun.com/drilistbox/article/details/79360912
[5]: http://blog.youkuaiyun.com/drilistbox/article/details/79368008
[6]: https://blog.youkuaiyun.com/drilistbox/article/details/79720859
…

文章目录

朴素贝叶斯方法是贝叶斯定理与特征条件独立假设相结合的分类方法。对于给定的训练数据，首先基于特征条件独立假设学习输入输出的联合概率分布；再利用贝叶斯定理算出后验概率最大的类。
#3.1 频率学派和贝叶斯学派
首先理解一下频率学派和贝叶斯学派在概率认知上的不同：
（1）频率学派：强调频率的“自然属性”，事件发生的概率是固定的，可使用事件在重复试验中发生的频率作为事件的发生概率。比如抛硬币，正反面的概率都是0.5。也可通过最大似然函数来确定参数分布。
（2）贝叶斯学派：任何事件具有随机性，事件发生的概率是不定的，0-100%都有可能，概率的根源不在于具体“事件”，而在于“观察者”对事件的认知状态。还是比如抛硬币，有人看到抛出的硬币是正面，那么当前硬币正面的概率为100%，反面的概率为0%。观察者获取的信息称为先验信息。
一个小例子来理解贝叶斯派的思想：
有一个人在那抛硬币，他抛好后叫你过来，让你猜猜硬币的正方面，由于你自己没有看到抛完后硬币的正反面，这时从尝试的角度来讲，你肯定觉得这个硬币不是正就是反的，所以你会说这个硬币无论正反面的概率都是0.5，这也符合最大熵模型理论：如果没有其他的参考信息，则选用熵最大的模型，即所有事件发生概率均匀分布。这时有好几个路人看到了抛硬币的过程，并且路人告诉你刚刚抛完的硬币正面朝上，这样的话你心里就会觉得硬币正面朝上的可能性要大一些。刚才上面的过程可以用贝叶斯方法来进行描述：
假设硬币正面朝上的事件为A，刚开始你什么都不知道，人家让你猜正反面，那么正面朝上的概率为P(A)=0.5，这是先验概率。接着发生了一个新的事件X：有路人告诉你硬币是正面朝上。那么现在假设硬币确实是正面朝上的，那路人说的话应该就是真的，P(X|A)就应该很接近1，不妨取为0.95，由于P(X|A)描述了抛硬币结果已知时路人所说话的可信度，因此称其为似然函数；但关键问题是，你并不知道路人的话说的对不对，因此要对路人的话的可信度做一个判断，按条件概率有P(X)=P(X|A)P(A)+P(X| _A)P(A)，其中P(A)=P( _{A)=0.5，P(X|}A)表示硬币是反面朝上时路人说的话的可信度，你也不清楚路人话里的真假是多少，就给P(X| _{A)赋一个0.5的肯能性吧，这样利用贝叶斯定理，得到后验概率有P(A|X)=P(A)P(X|A)/P(X)=P(A)P(X|A)/[P(A)P(X|A)+P(}A)P(X|~A)]=0.5 0.95/[0.50.95+0.5*0.5]=0.65，也就是说，你更倾向于认为硬币正面朝上。
#3.2 参数估计
这里多讲一下参数估计，在概率问题中，常常遇到如何从已有样本中获取信息并据此估计目标模型的参数，常用的方法有极大似然估计(ML估计)以及极大后验概率估计(MAP估计)。
##3.2.1 极大似然估计
已经发生的事件的概率应该是最大的才合理的。在这样的理念下，输出(y1, y1,…yN)在模型参数θ下的条件概率应该最大，从而可求出参数θ的值：
这里写图片描述

###3.2.2 极大后验概率估计

这里写图片描述
#3.3 朴素贝叶斯分类器
朴素贝叶斯是贝叶斯定理与特征条件独立假设相结合的产物，其中朴素对应着特征条件独立假设，贝叶斯对应着贝叶斯定理。条件独立性假设简化了问题，避免了贝叶斯求解时条件组合爆炸、样本稀疏的问题，对于上面的式(1.5)，进一步考虑特征条件独立假设，有：

这里写图片描述
这是朴素贝叶斯条件下的参数估计，条件独立假设可以使问题变得简单，但也会损失一定的准确率。我们可对它进行整理，转换为朴素贝叶斯分类器。朴素贝叶斯分类器通过训练数据集学习联合概率分布，从而得到先验概率和条件概率，据此可算得不同输入下不同输出的后验概率分布，后验概率最大的输出对应的类就是合理的类。比如有训练集：

在这里插入图片描述

#3.4 后验概率最大化的含义
朴素贝叶斯将实例分到后验概率最大的类中，这等价于期望风险最小化，假设选择0-1损失函数：

这里写图片描述

式中f(X)为分类决策函数，这时的条件期望风险函数为：

这里写图片描述

为了使期望风险最小化，只需对X=x逐个极小化，得到：

这里写图片描述

由此可见，期望风险最小化等价于后验概率最大化。这里有人可能会对期望风险、经验风险以及结构风险产生迷惑，我想补充说明一下：
（1）期望风险：对所有样本（包含未知样本和已知样本）的损失的期望：

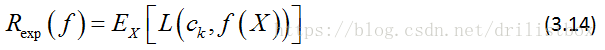
这里写图片描述

（2）经验风险：对训练样本（已知样本）的损失的期望：

这里写图片描述

（3）结构风险：在经验风险后加上一正则项，降低模型复杂度，防止过拟合：

这里写图片描述

3.5 小结

朴素贝叶斯是典型的生成学习方法。根据训练数据，利用极大似然估计或贝叶斯估计学习输入输出的联合概率分布，然后求得后验概率分布。
朴素贝叶斯的条件独立假设使得问题大大简化，同时也降低了对训练数据量的要求，这也使得模型精度下降（比如在处理文本或图像问题时，相邻文字或者像素都是相关的），分类性能不一定高。
朴素贝叶斯分类以后验概率最大的类作为输出类。
可以证明，后验概率最大等价于0-1损失函数时的期望风险最小化。
训练数据中的特征分布不一定能够涵括测试数据的特征分布，此时可以只计算涵括部分的特征概率，未涵括的不予考虑。
训练数据中的特征分布适当减少可以提升准确率，我们将图像二值化，原来特征分布范围为0-255的整数，二值化后非0及1。

文中实现了对MNIST数据的分类，对10000个测试数据测试后的准确率大概为84.41%，效果一般，不如KNN。
这里写图片描述

相应代码实现如下：

import sys;
import numpy as np
sys.path.append("./../Basic/")
import LoadData as ld

def NB(trainDataSet, trainLabels):
    P_X = []
    feature_set = []
    label_set = []
    for label in set(trainLabels.tolist()):
        temp = []
        feature_temp = []
        label_set.append(label)
        num = (trainLabels == label).astype('int32').sum()
        for feature_ind in range(trainDataSet.shape[1]):
#            temp.append([(trainLabels == label)[trainDataSet[:,feature_ind]==feature].astype('int32').sum()/num for feature in set(trainDataSet[:,feature_ind].tolist())])
            num2 = len(set(trainDataSet[:,feature_ind].tolist()))
            temp.append([((trainLabels == label)[trainDataSet[:,feature_ind]==feature].astype('int32').sum()+lambda_)/(num+lambda_*num2) for feature in set(trainDataSet[:,feature_ind].tolist())])
            feature_temp.append([feature  for feature in set(trainDataSet[:,feature_ind].tolist())])
        P_X.append(np.array(temp))
        feature_set.append(np.array(feature_temp))
    return P_X, feature_set, label_set
    
if __name__ == '__main__':
    iTrainNum      = 1000
    iTestNum       = 500
    lambda_ = 1.0
    eps = 100.0
    trainDataSet   = ld.getImageDataSet('./../MNISTDat/train-images-idx3-ubyte', iTrainNum, 1, 784)
    trainDataSet[trainDataSet<eps] = 0.0
    trainDataSet[trainDataSet>=eps] = 1.0

    trainLabels    = ld.getLabelDataSet('./../MNISTDat/train-labels-idx1-ubyte', iTrainNum)

    testDataSet    = ld.getImageDataSet('./../MNISTDat/t10k-images-idx3-ubyte', iTestNum, 1, 784)
    testDataSet[testDataSet<eps] = 0.0
    testDataSet[testDataSet>=eps] = 1.0

    testLabels     = ld.getLabelDataSet('./../MNISTDat/t10k-labels-idx1-ubyte', iTestNum)

#    trainDataSet = np.array([[1,1],[1,2],[1,2],[1,1],[1,1],[2,1],[2,2],[2,2],[2,1],[2,1],[3,2],[3,2],[3,2],[3,2],[3,1]])
#    trainLabels = np.array([-1,-1,1,1,-3,-1,-1,1,1,1,2,2,1,1,-1])
#    testDataSet = np.array([[2,1],[1,1],[2,2]])

    P_X, feature_set, label_set = NB(trainDataSet, trainLabels)    
    iRightNum = 0
    for ind in range(testDataSet.shape[0]):
        c = []
        for label in range(len(label_set)):
            p = 1.0
            for i in range(testDataSet.shape[1]):
                bool_ = feature_set[label][i] == testDataSet[ind][i]
                if(bool_.astype('int32').sum() == 0):
#                    print('sddf')
#                    p = 0.0
#                    break
                    p *= 1.0 #训练数据中的特征分布不一定能够涵括测试数据的特征分布，此时可以只计算涵括部分的特征概率，未涵括的不予考虑。
                else:
                    p *= np.array(P_X[label][i])[bool_][0]
            c.append(p)
        if(ind%50 == 49):  print(ind,'/',iTestNum)
        if(label_set[c.index(max(c))] == testLabels[ind]):
            iRightNum += 1
    print('precision rate:%0.2f' %(iRightNum*100.0/testDataSet.shape[0]))