循环神经网络（RNN）

前面总结的多层感知机（MLP）和卷积神经网络（CNN）本质上都是前馈神经网络，对于一组输入，得到一组输出，不会考虑前后输入数据之间的相关性。今天总结的循环神经网络（Recurrent Neural Network, RNN） 则是专门用于处理序列输入的神经网络，从直观上来看，序列输入（例如文本）是前后文相关的，而“循环”说明上一次的输出会重新作为这一次的输入，再次参与到运算中去，这样RNN就能够记忆之前的信息。

RNN网络结构

由于RNN是和“时间”（或者说“输入顺序”）有关的网络模型，因此下图的网络结构示意图中，左边部分表示了实际的网络结构，右边的展开部分表示了模型基于时间的计算过程。

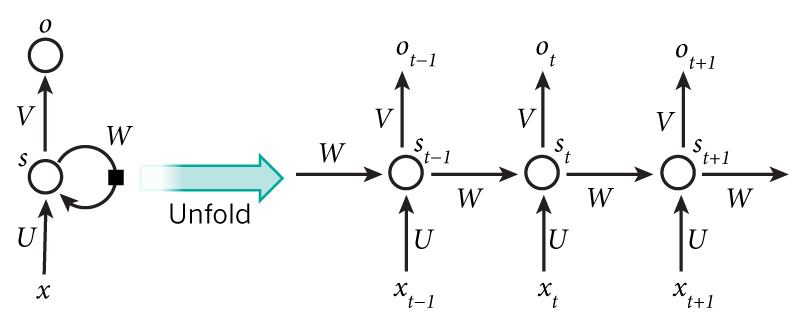
我们把RNN拆分成输入层、隐藏层和输出层。如果删掉循环连接（$W$对应的连接），那么上图(左)就变成了一个单纯的MLP，加上循环连接后，意味着模型必须保存上一时刻隐藏层的输出，并且在这一时刻作为隐藏层输入的一部分参与计算。用数学公式表示为
$$\begin{array}{rl}{o}_t& =g(V\cdot s_t)\\ s_t& =f(U\cdot x_t+W\cdot s_{t-1})。\end{array}\text{\hspace{1em}(1)}$$
公式中的符号在结构示意图中都可以找到。可以看出，隐藏层的输出$s_t$与当前输入和之前的输入都有关。另外参数$U,V,W$在任何时刻都是“共享”的。

训练方法（BPTT）

BPTT（Back-Propagation Through Time）本质上也是梯度下降的方法，只是由于引入了时间因素，当我们用误差函数对参数求梯度时，还应当追溯历史数据。假设$t$时刻误差函数为$L_t(o_t,y_t)$，那么“当前总误差”
$$L=\sum _{i=1}^t{L}_i,\text{\hspace{1em}(2)}$$
对于某个参数$W$，通过求偏导$\frac{\partial L}{\partial W}$来对参数进行更新。

因为$V$与时间无关，所以其偏导也比较简单；$U,W$的偏导则相对复杂，举个栗子，根据公式(1)，$L_2$对$W$的偏导
$$\frac{\partial L_2}{\partial W}=\frac{\partial L_2}{\partial s_2}\frac{\partial s_2}{\partial W}+\frac{\partial L_2}{\partial s_2}\frac{\partial s_2}{\partial s_1}\frac{\partial s_1}{\partial W}，\text{\hspace{1em}(3)}$$
这是在时刻$2$时，考虑时间序列的偏导结果，不难想象，对于$L_t$，需要依次考虑$s_t,...,s_1$（因为他们都是$W$的函数）对$W$的偏导然后累加起来。而$\frac{\partial L}{\partial W}$又是对$\frac{\partial L_t}{\partial W}$的一层累加。好在$\frac{\partial L}{\partial W}$的总公式最后能够化简，这里不详细追究了。

公式(1)中的$g,f$是激活函数，根据以前的经验，$t$长度的链式求导容易导致梯度消失或者梯度爆炸。

其它

粗略看了一下LSTM和Transformer，目前暂时没用到这些，先挖个坑，以后有时间或者需要的时候再补~