2.题目描述:
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一 项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1
F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。
示例 1:
输入:n = 2
输出:1
解释:F(2) = F(1) + F(0) = 1 + 0 = 1
示例 2:
输入:n = 3
输出:2
解释:F(3) = F(2) + F(1) = 1 + 1 = 2
示例 3:
输入:n = 4
输出:3
解释:F(4) = F(3) + F(2) = 2 + 1 = 3
提示:
0 <= n <= 30
3. 解法(暴搜 -> 记忆化搜索 -> 动态规划):
算法思路:
暴搜:
a. 递归含义:给 dfs 一个使命,给他一个数 n ,返回第 n 个斐波那契数的值;
b. 函数体:斐波那契数的递推公式;
c. 递归出口:当 n == 0 或者 n == 1 时,不用套公式。
记忆化搜索:
a. 加上一个备忘录;
b. 每次进入递归的时候,去备忘录里面看看;
c. 每次返回的时候,将结果加入到备忘录里面。
动态规划:
a. 递归含义 -> 状态表示;
b. 函数体 -> 状态转移方程;
c. 递归出口 -> 初始化。
Java算法代码:
class Solution {
int memo [] = new int [31];
int dp [] = new int [31];
public int fib(int n) {
//动态规划
// dp[0] = 0; dp[1] = 1;
// for(int i = 2; i<= n; i++)
// dp[i] = dp[i-1] + dp[i-2];
// return dp[n];
Arrays.fill(memo, -1);
return dfs(n);
}
//记忆和搜索
int dfs (int n){
if(memo[n] != -1){
return memo[n];//直接去备忘录中拿值
}
if( n == 0 || n ==1){
memo[n] = n; //记录到备忘录中。
return n;
}
memo[n] = dfs(n-1) + dfs(n -2); //这里记录到备忘录中
return memo[n];
}
}运行结果:
递归展开:
这里笔者提供了三种方法,滚动数组(也就是动态规划)
提供了暴力搜索
然后提供了暴力搜索的优化(记忆化搜索)
这里是笔者给一个同学进行讲解,画的有点潦草。
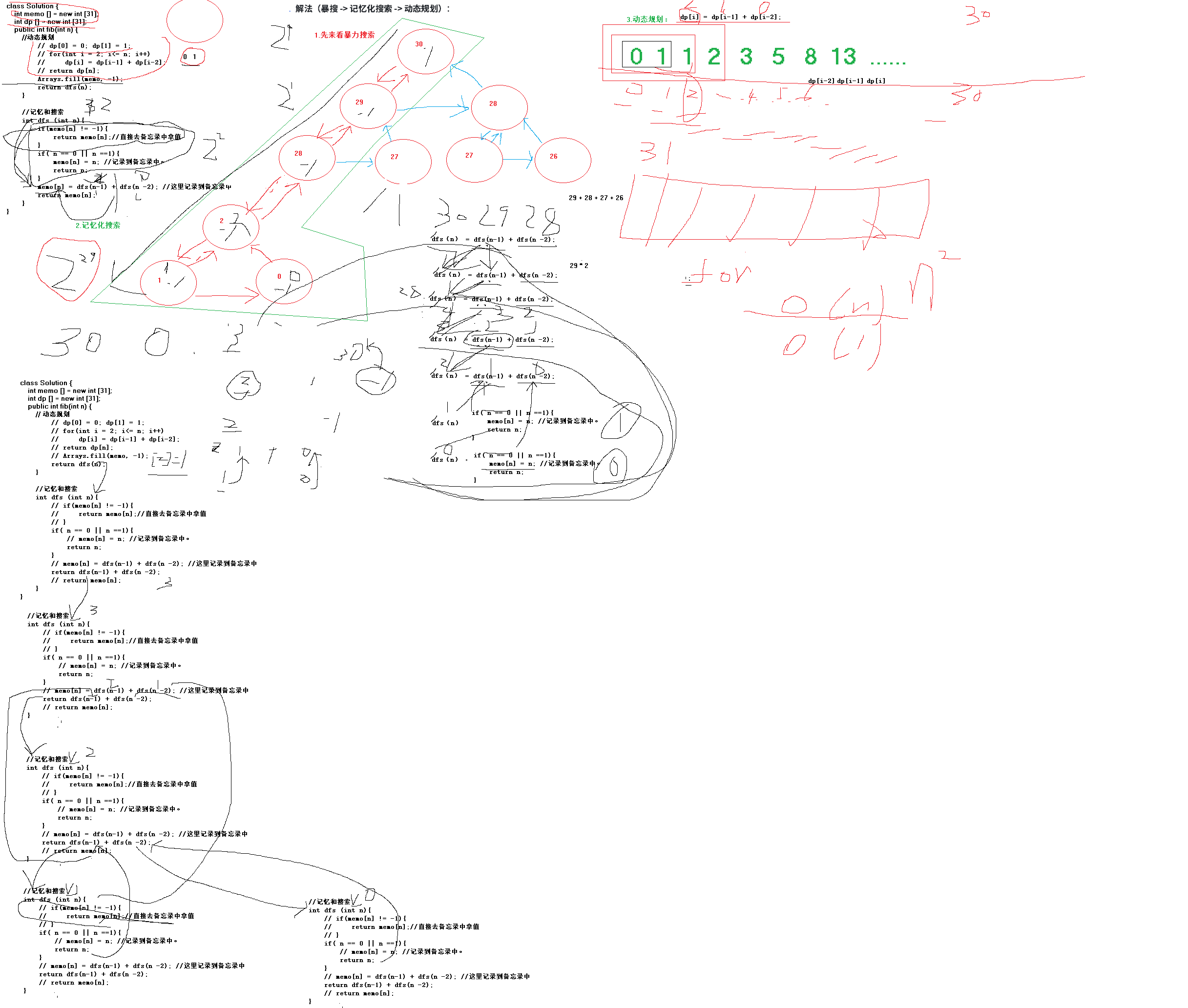
逻辑展开:
这个题目是非常简单的,比如最容易想到的暴力搜索(也就是递归的方法)
比较难想的是优化和动态规划的办法。
另外的办法,体现了,不同的思维方式。
---------------------------------------------------------------------------------------------------------------------------------
记住,相信你的递归函数,它可以做到!
记住,不理解时候,去尝试手动展开!
记住,逻辑展开(你不可能对所有的题目都进行手动展开)!




















 656
656

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








