2.题目描述:
有一个 m × n 的矩形岛屿,与 太平洋 和 大西洋 相邻。 “太平洋” 处于大陆的左边界和上边界,而 “大西洋” 处于大陆的右边界和下边界。
这个岛被分割成一个由若干方形单元格组成的网格。给定一个 m x n 的整数矩阵 heights , heights[r][c] 表示坐标 (r, c) 上单元格 高于海平面的高度 。
岛上雨水较多,如果相邻单元格的高度 小于或等于 当前单元格的高度,雨水可以直接向北、南、东、西流向相邻单元格。水可以从海洋附近的任何单元格流入海洋。
返回网格坐标 result 的 2D 列表 ,其中 result[i] = [ri, ci] 表示雨水从单元格 (ri, ci) 流动 既可流向太平洋也可流向大西洋 。
示例 1:
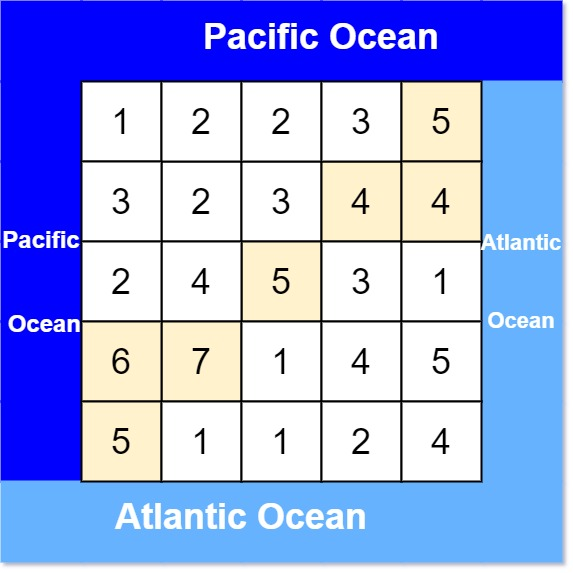
输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]
示例 2:
输入: heights = [[2,1],[1,2]]
输出: [[0,0],[0,1],[1,0],[1,1]]
提示:
m == heights.length
n == heights[r].length
1 <= m, n <= 200
0 <= heights[r][c] <= 10^5
3. 解法:
算法思路:
正难则反。
如果直接去判断某一个位置是否既能到大西洋也能到太平洋,会重复遍历很多路径。
我们反着来,从大西洋沿岸开始反向dfs ,这样就能找出那些点可以流向大西洋;同理,从太平洋沿
岸也反向 dfs ,这样就能找出那些点可以流向太平洋。那么,被标记两次的点,就是我们要找的结
果。
Java算法代码:
class Solution {
int m,n;
int []dx = {0,0,1,-1};
int []dy = {1,-1,0,0};
public List<List<Integer>> pacificAtlantic(int[][] h) {
m = h.length;n=h[0].length;
boolean[][] pac = new boolean[m][n];
boolean[][] atl = new boolean[m][n];
//1.先处理pac洋
for(int j = 0; j<n;j++) dfs(h,0,j,pac);
for(int i = 0; i<m;i++) dfs(h,i,0,pac);
//2.再处理atl杨
for(int i = 0; i<m;i++) dfs(h,i,n-1,atl);
for(int j = 0; j<n;j++) dfs(h,m-1,j,atl);
//3.提取结果
List<List<Integer>> ret = new ArrayList<>();
for(int i =0;i<m;i++)
for(int j = 0; j<n; j++)
if(pac[i][j] &&atl[i][j]){
List<Integer> tmp = new ArrayList<>();
tmp.add(i);tmp.add(j);
ret.add(tmp);
}
return ret;
}
public void dfs(int [][] h, int i, int j, boolean[][] vis){
vis[i][j] = true;
for(int k =0;k<4;k++){
int x = i + dx[k], y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && h[x][y] >=h[i][j]){
dfs(h, x, y, vis);
}
}
}
}运行结果:
递归展开:需要注意的是,这里的前面的递归开始的地方,要认真的看题目的图片,来进行理解.理解这里的两个大洋的范围,
以及倒反天罡的思维。
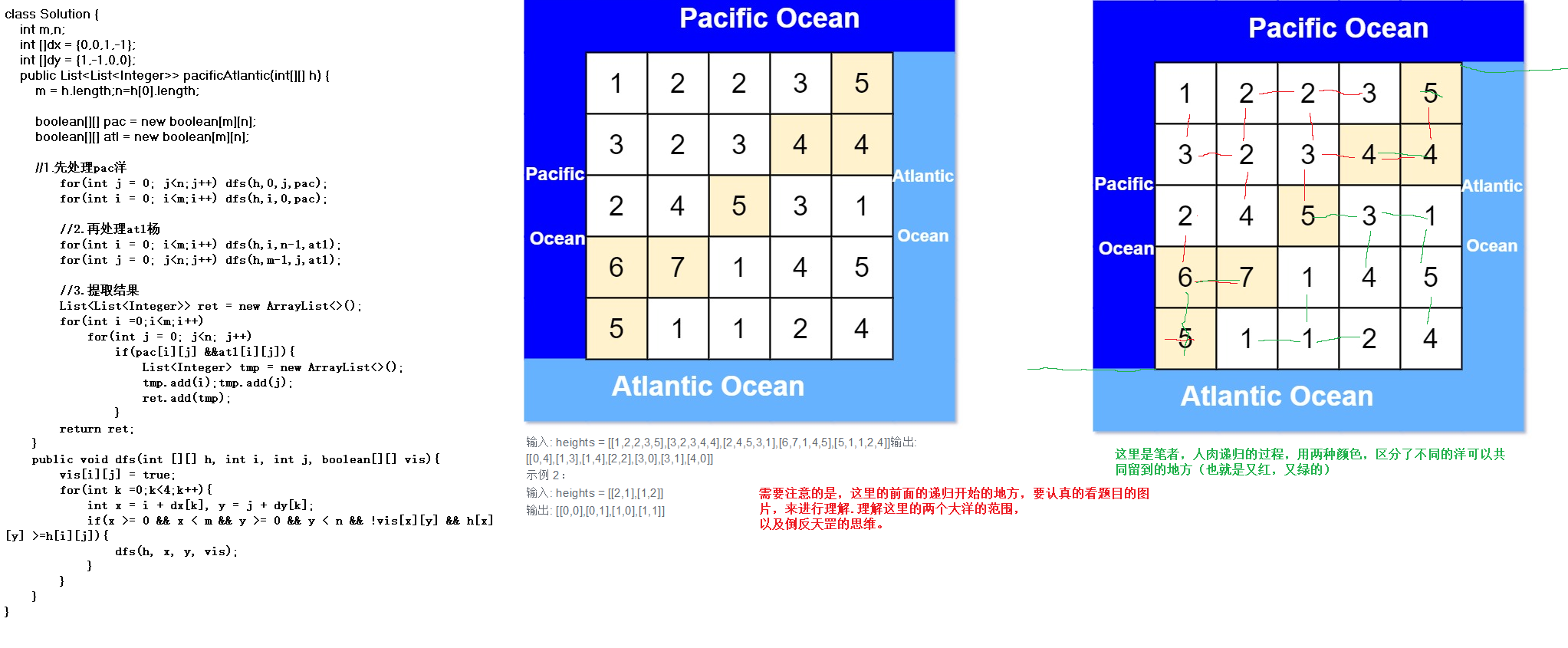
逻辑展开:笔者了解细节之后,就会知道怎么画出那个红色、绿色的杠杠图。然后就完全明白这个题目了。
---------------------------------------------------------------------------------------------------------------------------------
记住,相信你的递归函数,它可以做到!
记住,不理解时候,去尝试手动展开!
记住,逻辑展开(你不可能对所有的题目都进行手动展开)!





















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








