1.题目链接:
2.题目描述:
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数 字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种 组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
• 示例 1:
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。7 也是一个候选, 7 = 7 。
仅有这两种组合。
•示例 2:
输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]
• 示例 3:
输入: candidates = [2], target = 1
输出: []
• 提示:
1 <= candidates.length <= 30
2 <= candidates[i] <= 40
candidates 的所有元素 互不相同
1 <= target <= 40
3. 解法:
算法思路:
candidates 的所有元素 互不相同,因此我们在递归状态时只需要对每个元素进行如下判断:1. 跳过,对下一个元素进行判断;
2. 将其添加至当前状态中,我们在选择添加当前元素时,之后仍可以继续选择当前元素(可以重复选择同一元素)。
•因此,我们在选择当前元素并向下传递下标时,应该直接传递当前元素下标。
递归函数设计:void dfs(vector<int>& candidates, int target, vector<vector<int>>& ans, vector<int>& combine, int idx)
参数:target(当前状态和与目标值的差),idx(当前需要处理的元素下标);
返回值:无;
函数作用:向下传递两个状态(跳过或者选择当前元素),找出所有组合使得元素和为目标值。
递归函数流程如下:
1. 结束条件:
a. 当前需要处理的元素下标越界;
b. 当前状态的元素和已经与目标值相同;
2. 跳过当前元素,当前状态不变,对下一个元素进行处理;
3. 选择将当前元素添加至当前状态,并保留状态继续对当前元素进行处理,递归结束时撤销添加操作。
Java算法代码:
class Solution {
int aim;
List<Integer> path;
List<List<Integer>> ret;
public List<List<Integer>> combinationSum(int[] nums, int target) {
path = new ArrayList<>();
ret = new ArrayList<>();
aim = target;
dfs(nums, 0, 0);
return ret;
}
public void dfs(int[] nums, int pos, int sum){
if(sum == aim){
ret.add(new ArrayList<>(path));
return;
}
if(sum>aim || pos == nums.length) return;
//枚举nums[pos]使用多少个
for(int k =0;k*nums[pos]+sum<=aim;k++){
if(k!=0) path.add(nums[pos]);
dfs(nums,pos+1,sum+k*nums[pos]);
}
//恢复现场
for(int k = 1; k * nums[pos] + sum <= aim; k++){
path.remove(path.size() - 1);
}
}
}运行结果:
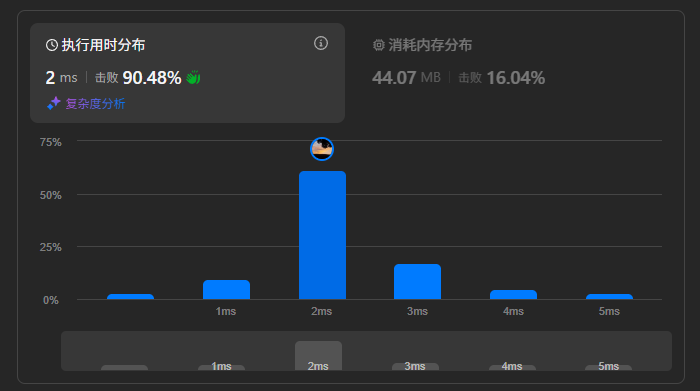
递归展开:这道题请认真展开,因为确实有难度,笔者自己就错了好几次,然后最终看懂了这个细节。进而使用逻辑展开的方式得到了所有的结果(以及顺序)。
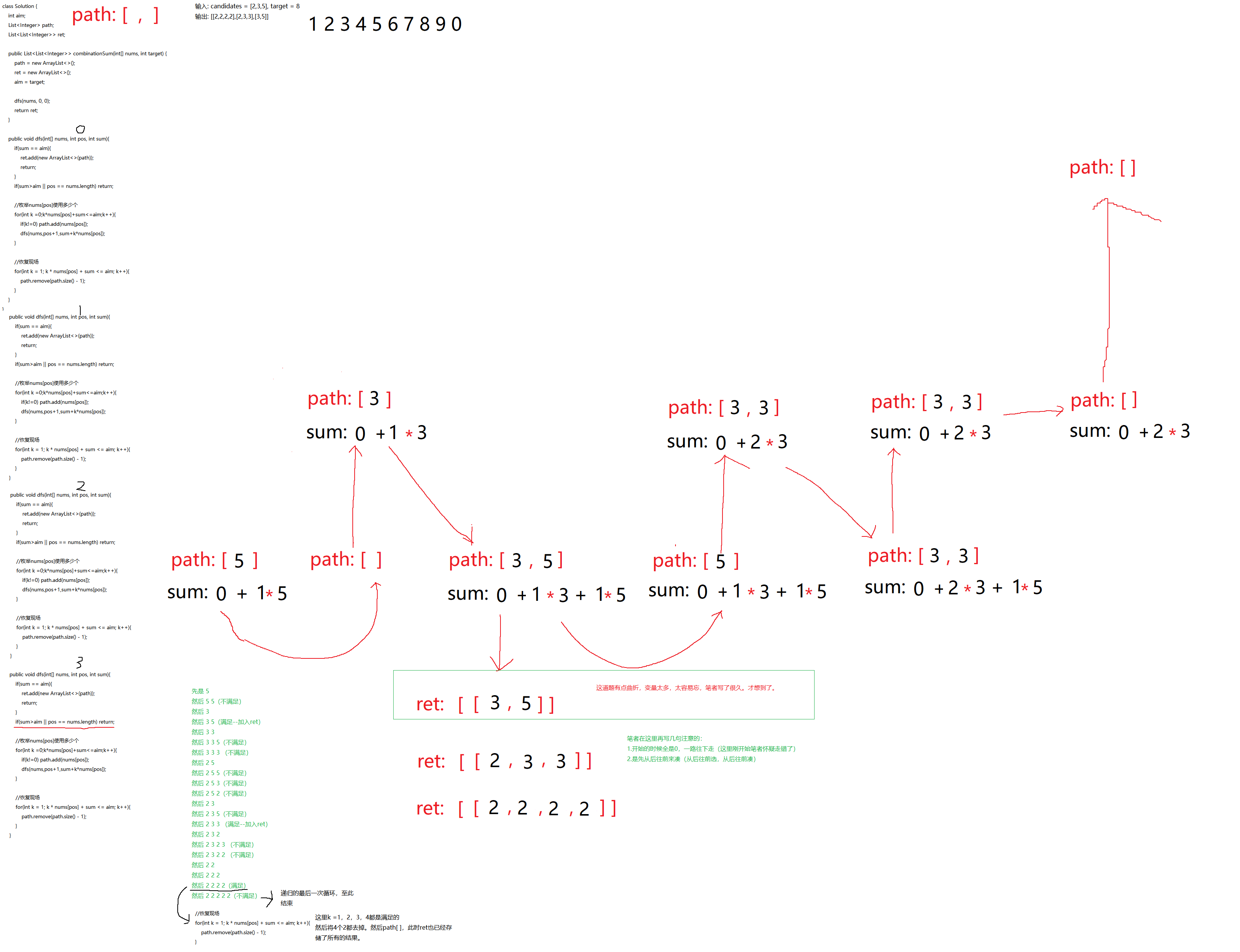
逻辑展开:这里来看看,这里笔者有点笔误,这里实际上ret的东西是这三个,path的某一刻都存储了这三个值。
当你能看懂笔者这里的一排数字推理,你就懂了,如果发现笔者哪里写错了,请指出。

---------------------------------------------------------------------------------------------------------------------------------
记住,相信你的递归函数,它可以做到!
记住,不理解时候,去尝试手动展开!
记住,逻辑展开(你不可能对所有的题目都进行手动展开)!





















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








