1.题目链接:
2.题目描述:
给你一个二叉树的根节点root,按任意顺序,返回从根节点到叶子节点的路径。
叶子节点:是指没有子节点的节点。
示例1:
输入:root = [1,2,3,null,5]
输出:["1->2->5","1->3"]
示例2:
输入:root = [1]
输出:["1"]
提示:
树中节点的数目在范围 [1, 100] 内
-100 <= Node.val <= 100
3.解法(回溯):
算法思路:
使用深度优先遍历(DFS)求解。
路径以字符串形式存储,从根节点开始遍历,每次遍历时将当前节点的值加入到路径中,如果该节点为叶子节点,将路径存储到结果中。否则,将 "->" 加入到路径中并递归遍历该节点的左右子树。定义一个结果数组,进行递归。递归具体实现方法如下:
1. 如果当前节点不为空,就将当前节点的值加入路径 path 中,否则直接返回;
2. 判断当前节点是否为叶子节点,如果是,则将当前路径加入到所有路径的存储数组 paths 中;
3. 否则,将当前节点值加上 "->" 作为路径的分隔符,继续递归遍历当前节点的左右子节点。
4. 返回结果数组。
•特别地,我们可以只使用一个字符串存储每个状态的字符串,在递归回溯的过程中,需要将路径中的当前节点移除,以回到上一个节点。
具体实现方法如下:
1. 定义一个结果数组和一个路径数组。
2. 从根节点开始递归,递归函数的参数为当前节点、结果数组和路径数组。
a. 如果当前节点为空,返回。
b. 将当前节点的值加入到路径数组中。
c. 如果当前节点为叶子节点,将路径数组中的所有元素拼接成字符串,并将该字符串存储到结果 数组中。
d. 递归遍历当前节点的左子树。
e. 递归遍历当前节点的右子树。
f. 回溯,将路径数组中的最后一个元素移除,以返回到上一个节点。
3. 返回结果数组。
Java算法代码:
class Solution {
List<String> ret;
public List<String> binaryTreePaths(TreeNode root) {
ret = new ArrayList<>();
dfs(root, new StringBuffer());
return ret;
}
void dfs(TreeNode root,StringBuffer _path){
StringBuffer path = new StringBuffer(_path);
path.append(Integer.toString(root.val));
if(root.left == null && root.right == null){
ret.add(path.toString());
return;
}
path.append("->");
if(root.left != null) dfs(root.left,path);
if(root.right != null) dfs(root.right,path);
}
}运行结果:
递归展开:
请注意这里为什么new StringBuffer而不是,使用一个全局变量呢?
简单说,只要得到过就能存储(当遍历到底,得到了一条完整路径,直接存储ret(这个是全局的)。
因为是局部变量,所以在一次函数调用结束(既得到了完整路径(暂存)--》ret),又没有改变原本的path。也就是说,帮我们进行回溯了。或者说是避免了回溯。
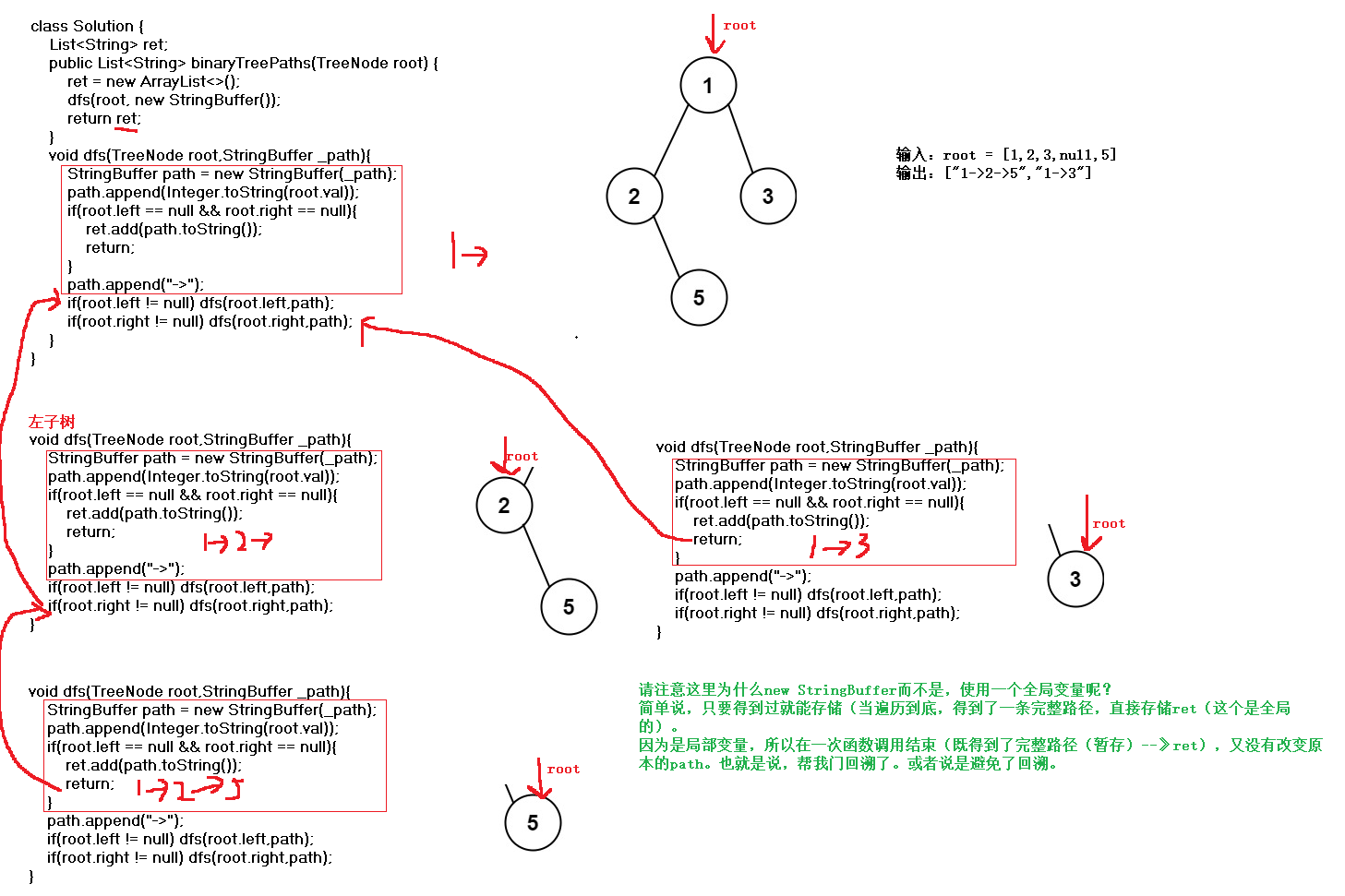
逻辑展开:

这道题的细节:回溯体现在哪里呢??你发现自己好像什么都没做?
但是代码中的这个一个全局变量ret和一个局部变量的设计,需要读者去好好的体会。
---------------------------------------------------------------------------------------------------------------------------------
记住,相信你的递归函数,它可以做到!
记住,不理解时候,去尝试手动展开!
记住,逻辑展开(你不可能对所有的题目都进行手动展开)!




















 2184
2184

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








