1.题目链接:
给你一个二叉树的根节点 root,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
| • | 节点的左子树只包含 小于 当前节点的数。 |
示例 1:
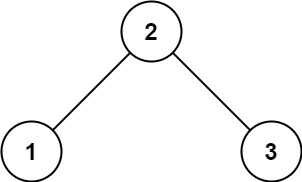
输入:root = [2,1,3]
输出:true
示例 2:
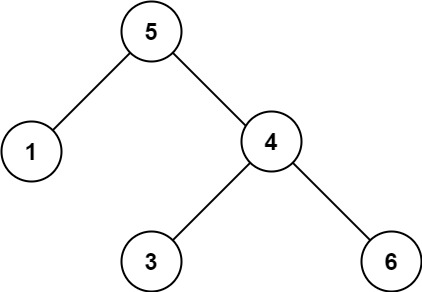
输入:root = [5,1,4,null,null,3,6]
输出:false
解释:根节点的值是 5 ,但是右子节点的值是 4 。
3. 解法(利用中序遍历):
中序遍历按照左子树、根节点、右子树的顺序遍历二叉树的所有节点,通常用于二叉搜索树相关题目。
算法思路:
如果一棵树是二叉搜索树,那么它的中序遍历的结果一定是一个严格递增的序列。
因此,我们可以初始化一个无穷小的全局变量,用来记录中序遍历过程中的前驱结点。那么就可以在中序遍历的过程中,先判断是否和前驱结点构成递增序列,然后修改前驱结点为当前结点,传入下一层的递归中。
算法流程:
1. 初始化一个全局的变量 prev,用来记录中序遍历过程中的前驱结点的 val;
2. 中序遍历的递归函数中:
a. 设置递归出口:root == nullptr 的时候,返回 true;
b. 先递归判断左子树是否是二叉搜索树,用 retleft 标记;
c. 然后判断当前结点是否满足二叉搜索树的性质,用 retcur 标记:
▪ 如果当前结点的 val 大于 prev,说明满足条件,retcur 改为 true;
▪ 如果当前结点的 val 小于等于 prev,说明不满足条件,retcur 改为 false;
d. 最后递归判断右子树是否是二叉搜索树,用 retright 标记;
3. 只有当 retleft、 retcur 和 retright 都是 true 的时候,才返回 true。
Java算法代码:
class Solution {
long prev = Long.MIN_VALUE;
public boolean isValidBST(TreeNode root) {
if(root == null) return true;
boolean left = isValidBST(root.left);
if(left == false) return false;//这里其实是减枝,如果已经发现左子树不是搜索二叉树了,就返回false,因为这完整的树也不可能是搜索二叉树了。
boolean cur = false;
if(root.val > prev) cur =true;
if(cur == false) return false;
prev = root.val;
boolean right = isValidBST(root.right);
return left && cur && right;
}
}结果:
递归展开: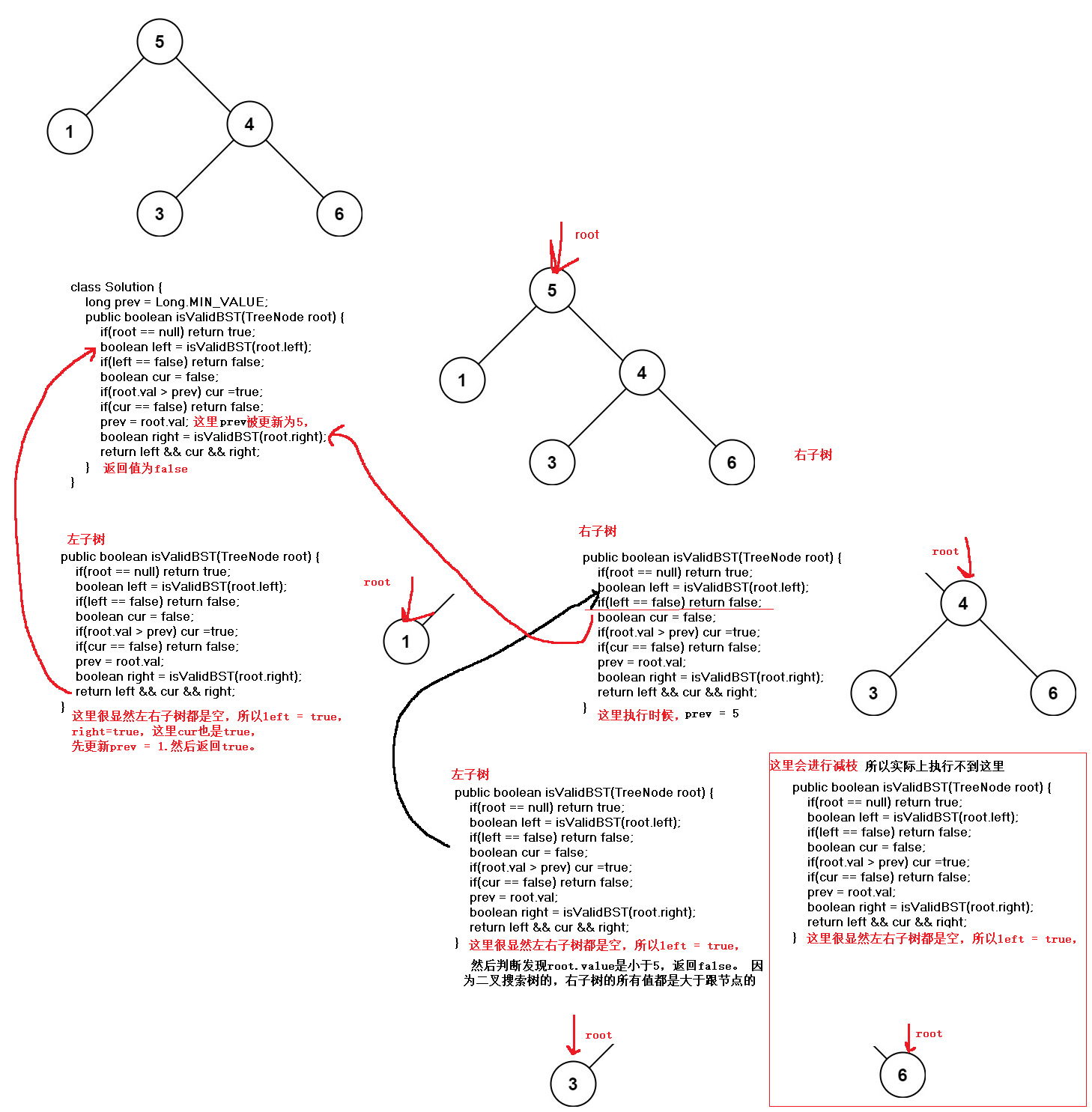
逻辑展开:

在学习时候,需要去尝试手动展开!这是帮助你理解,并且建立你对递归函数的信心。
而逻辑展开,是你对递归函数的宏观理解,只有你相信你的递归函数是对的,你才能对逻辑展开的结果信任。
---------------------------------------------------------------------------------------------------------------------------------
记住,相信你的递归函数,它可以做到!
记住,不理解时候,去尝试手动展开!
记住,逻辑展开(你不可能对所有的题目都进行手动展开)!




















 174万+
174万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








