此讲义课件共21讲,为我和别人合作的《从零掌握GNSS、RTK定位》课程讲义,当然也有收费的配套视频讲解,详情关注我个人公众号 GNSS和自动驾驶。
csdn对word粘贴来的公式支持不好,显示可能有点奇怪,可以去公众号看历史推文。
4.1 电磁波测距原理

如果已知从A发射到B反射到A接收到信号之间的用时为 t
那么有AB之间的距离S

如果已知波长为![]() , 从A发射到B反射到A接收到信号之间的一共有
, 从A发射到B反射到A接收到信号之间的一共有 周期
周期
那么有AB之间的距离S

-
-
卫星信号
-
- 载波
可运载调制信号的高频振荡波称为载波。
在无线电通信中, 为了更好地传送信息, 我们往往将这些信息调制在高频的载波上, 然后再将这些调制波播发出去, 而不是直接发射这些信息。
- 测距码
测距码是用于测定从卫星至接收机间的距离的二进制码。
GPS 卫星中所用的测距码从性质上讲属于伪随机噪声码。它们看似一组杂乱无章的随机噪声码, 其实是按照一定规律编排起来的、可以复制的周期性的二进制序列,且具有类似于随机噪声码的自相关特性。
- 导航电文/数据码
导航电文是由 GPS 卫星向用户播发的一组反映卫星在空间的位置、卫星的工作状态、卫星钟的修正参数、电离层延迟修正参数等重要数据的二进制代码, 也称数据码( D 码) 。


4.3 伪距观测量
所谓伪距观测量,实际上是测量GPS卫星发射的测距码信号(C/A码或P码)到达用户接收机天线的电磁波传播时间![]() 。因此,这种观测方法也称为时间延迟测量。
。因此,这种观测方法也称为时间延迟测量。

![]() 为卫星
为卫星![]() 发射信号时的卫星星钟时刻;
发射信号时的卫星星钟时刻;![]() 为用户接收机
为用户接收机![]() 接收到
接收到![]() 时刻卫星发射之码信号的站钟时刻;
时刻卫星发射之码信号的站钟时刻;
![]() 为卫星星钟tj
为卫星星钟tj![]() 时刻发射之码相位;
时刻发射之码相位;![]() 为用户接收机于站钟
为用户接收机于站钟![]() 时刻复制的码相位。
时刻复制的码相位。
在卫星星钟和接收机站钟完全同步的情况下,同时忽略大气对无线电信号折射的影响,所得到的时间延迟量τ![]() 与光速c相乘,即得到卫星到GPS接收机天线之间的几何距离(或称真距离)。
与光速c相乘,即得到卫星到GPS接收机天线之间的几何距离(或称真距离)。
![]()
实际上,卫星的星钟和接收机的站钟不可能完全同步,同时无线电信号经过电离层和对流层时由于折射的影响也均有附加延迟,所以实际测量得到的距离不是真实的距离,而是含有误差的伪距,以符号![]() 表示。
表示。
![]() 代表卫星
代表卫星![]() 到接收机
到接收机![]() 的伪距观测量。
的伪距观测量。
接收机复制的测距码和接收到的卫星发射的测距码在时间延迟器的作用下相关时(对齐时),根据经验,相关精度约为码元宽度的1%。对于C/A码来讲,由于其码元宽度约为293m,所以其观测精度为2.9m。
而对于P码来讲,其码元宽度是C/A码码元宽度的1/10(29.3m),故其测量精度也就比C/A码的测码精度高10倍,为0.29m。因此,有时也将C/A码称为粗码,P码称为精码。
但对于粗码来说,采用窄相关间隔( Narrow Correlator Spacing) 技术后测距精度可达分米级, 与精码的测距精度大体相当。
4.4 载波观测量
载波只是一种单纯的余弦波,不带有任何的识别标志,所以在第一次进行载波相位测量时,接收机实际上能测定的只是不足整周的小数部分![]() 。
。
初始观测历元![]() ,载波的观测值为(单位为周)
,载波的观测值为(单位为周)
![]()
其中![]() 为整周模糊度。
为整周模糊度。
那么在下一个![]() 时刻
时刻
i
其中![]() 为由时刻
为由时刻![]() 到
到![]() 接收机整周计数部分,可以通过信号跟踪计算得到。
接收机整周计数部分,可以通过信号跟踪计算得到。

由于载波频率高,波长短,所以载波相位测量精度高。若测相精度为1%,则对于L1载波来讲,波长![]() ,测距精度为0.19cm;对于L2载波来讲,波长
,测距精度为0.19cm;对于L2载波来讲,波长![]() ,其测距精度为0.24cm。由此可见,利用载波相位观测值进行定位,精度要比伪距定位精度高几个数量级,故载波相位观测方法常被用于精密定位和载体姿态测量中。
,其测距精度为0.24cm。由此可见,利用载波相位观测值进行定位,精度要比伪距定位精度高几个数量级,故载波相位观测方法常被用于精密定位和载体姿态测量中。
4.5 多普勒观测量
如图所示,一个静止不动的信号发射塔向外播发频率为f![]() 的信号,而接收机以速度v
的信号,而接收机以速度v![]() 运行,那么由于信号发射源与接收机之间相对运动所引起的多普勒效应,接收机接收到的信号频率f
运行,那么由于信号发射源与接收机之间相对运动所引起的多普勒效应,接收机接收到的信号频率f![]() 发生了变化,它不再等于信号的发射频率f
发生了变化,它不再等于信号的发射频率f![]() ,而是f+fd
,而是f+fd![]() ,其中fd
,其中fd![]() 称为多普勒频移,它定义为信号接收频率fr
称为多普勒频移,它定义为信号接收频率fr![]() 与信号发射频率f
与信号发射频率f![]() 之间的差异,即
之间的差异,即
fd=fr-f![]()
同时如果我们已知载波的运动速度v![]() 和信号入射角度β
和信号入射角度β![]()
fd=vλcosβ=vcfcosβ
式中,λ![]() 是与信号发射频率f
是与信号发射频率f![]() 相对应的信号波长,c
相对应的信号波长,c![]() 为光速,而β
为光速,而β![]() 为信号入射角,即从接收机的运动方向到信号人射方向的夹角。
为信号入射角,即从接收机的运动方向到信号人射方向的夹角。
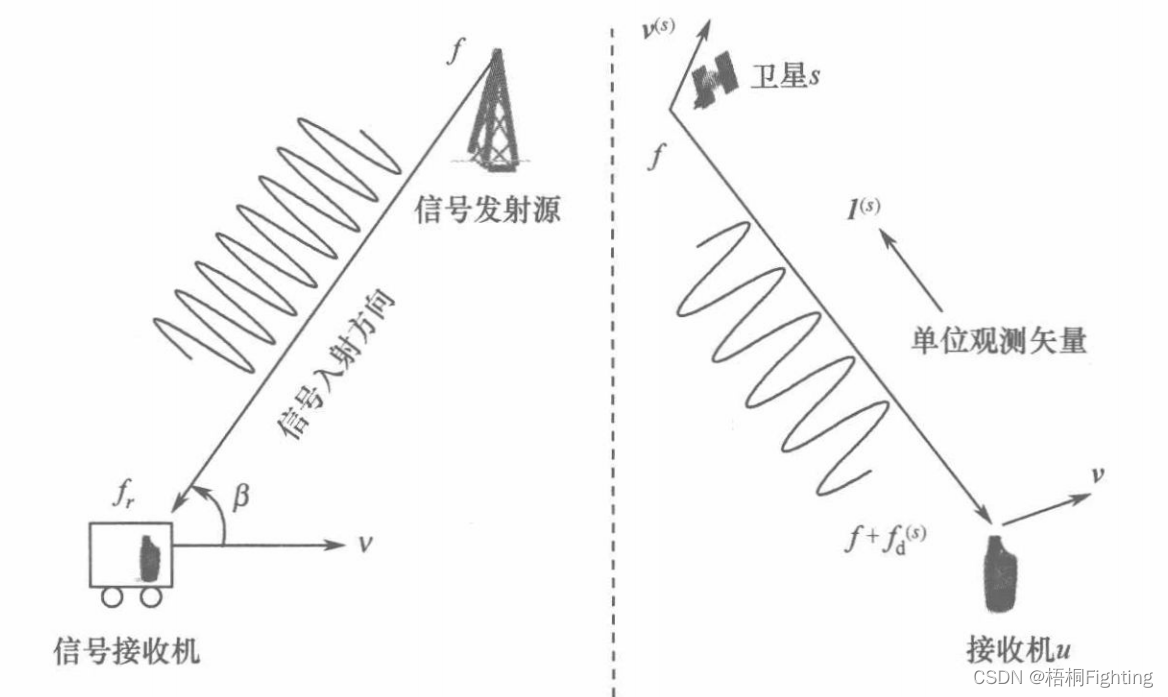
我们很容易进一步推导出在移动型信号发射源情形下的多普勒频移值计算公式。如图所示,假设作为移动型信号发射源的卫星s![]() 的运行速度向量为vs
的运行速度向量为vs![]() ,发射信号的载波频率为f
,发射信号的载波频率为f![]() 而接收机的运动速度向量为v
而接收机的运动速度向量为v![]() ,那么接收信号的载波多普勒频移值fds
,那么接收信号的载波多普勒频移值fds![]() 为
为

其中为卫星s![]() 在接收机u
在接收机u![]() 处的单位观测向量。如果我们已知卫星信号的多普勒频移fds
处的单位观测向量。如果我们已知卫星信号的多普勒频移fds![]() ,并利用卫星星历计算出卫星速度vs
,并利用卫星星历计算出卫星速度vs![]() ,那么接收机的运动速度就应该能被计算出来,实现接收机定速。
,那么接收机的运动速度就应该能被计算出来,实现接收机定速。







 本文详细介绍了GPS定位中的电磁波测距原理,包括伪距观测量(基于测距码的时间延迟)、载波观测量(高精度波长对应)以及多普勒观测量(运动物体间的频率变化)。C/A码和P码的精度对比以及载波相位在精密定位中的应用也被提及。
本文详细介绍了GPS定位中的电磁波测距原理,包括伪距观测量(基于测距码的时间延迟)、载波观测量(高精度波长对应)以及多普勒观测量(运动物体间的频率变化)。C/A码和P码的精度对比以及载波相位在精密定位中的应用也被提及。
















 437
437

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








