传输协议优化的博弈三角

以下是一个传输协议优化的博弈三角：

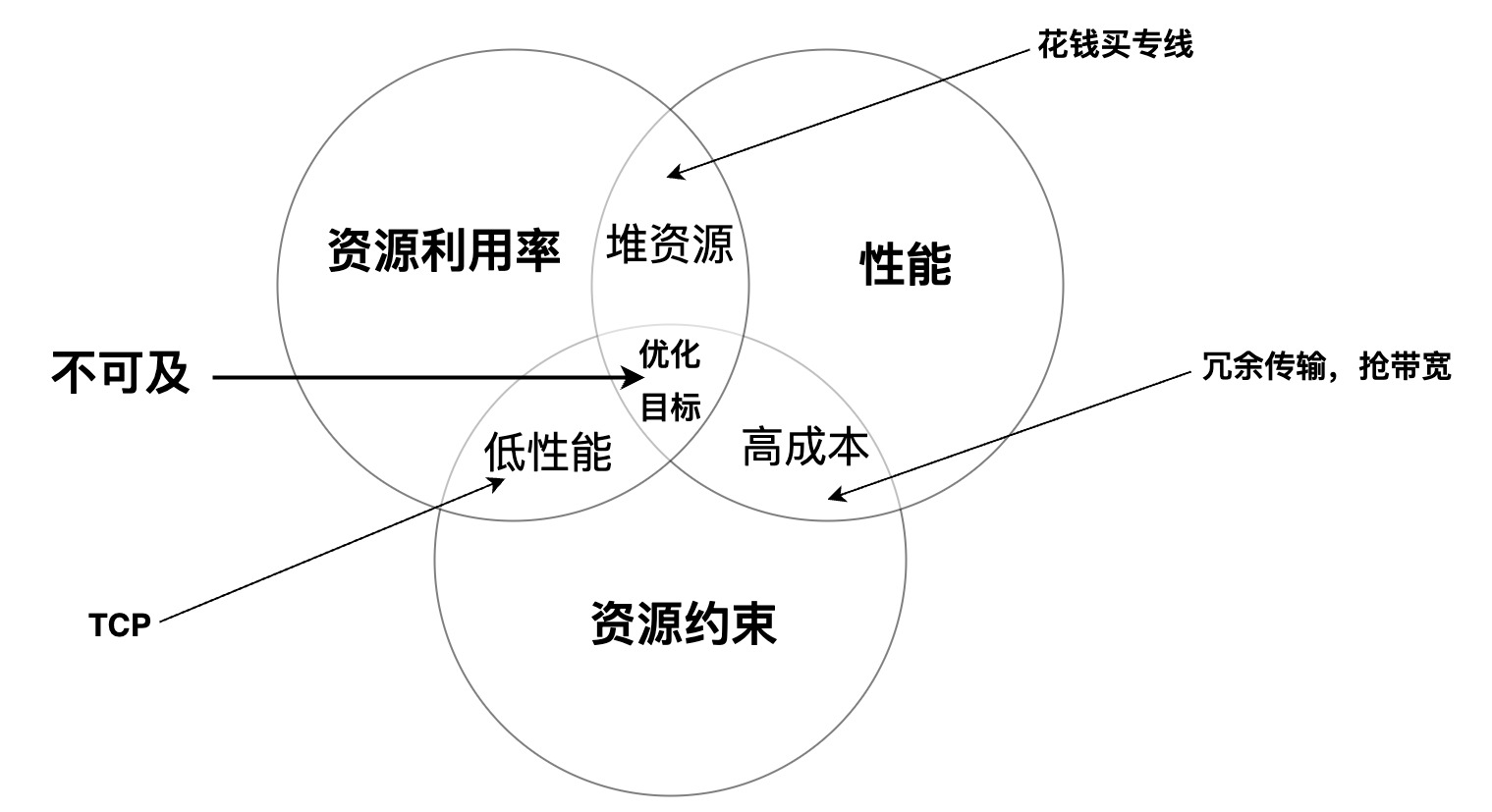
大致解释一下。

早期的文章中我不断重申一个观点，即资源约束了性能的上限，而性能的下限则由你的协议和算法决定。最理想的协议和算法只能让传输性能无限接近上限而无法超越，换句话举例说，弱网再优化也不会好到哪儿去，而带宽资源充足的网络即使不优化，传输性能也不会太差，反而越优化越糟糕：

好的优化效果对协议的演进理解以及算法水平要求极高，并非单纯某项或某几项技术可以覆盖。

从社会学和博弈论视角看，由于诱导流量等因素，Little 系统倾向于填满所有空间，网络流量一定会以资源供给为统计期望，而方差则取决于统计突发模型，因此根本不存在过度配置的网络，网络几乎一定会拥塞。

传输优化中一个很重要的点就是将拥塞造成的损耗降至最低，这个损耗不仅仅包含性能损耗，还有成本损耗。如果一个算法在拥塞后的丢包重传中采用激进的方式，那么恰恰只是将性能损耗转嫁到了成本损耗，难点不是如何提高性能，而是在不增加成本的前提下提高性能。

所以说我经常听到一些一听就不靠谱的论断，比如 PR 自家的协议或面试过程中，算法可以提升多少倍的性能，同时又不增加成本，这种属于懂一点但又不是真懂的，但如果看明白了这个博弈三角，就肯定谨言慎行了。

早些年我曾经给出过一个关于传输协议更微观的博弈三角：

其中因果关联，类似文初宏观视角分析。

此外，还有性能，成本，可靠性组成的博弈三角，甚至经典的 CAP 定理描述的一致性，可用性，分区容错性组成的博弈三角，这个三角定义了互联网本身，P 客观存在，C，A 之间做 trade-off，而 P 的客观性是定义的，互联网设计之初，本身就是需要分区容错，如果没了这个特性，类似主板那样，就无法抵御核打击了。

任何博弈三角，当你横向展开它后，会发现第四个维度，即资源约束，比如在 CAP 定理中，对资源的假设也是随时可以由于故障而失效的。资源约束永远决定了该博弈均衡最好结果的上限，但你可以通过算法自己决定博弈方的权重比例，以倾向于特定的一方。比方说计费方式如何影响优化算法，带宽的长程依赖如何给优化算法更多信息，而你必须利用好这些信息，而不是误用它们适得其反。

写此文的目的是澄清一个观点，传输优化的博弈三角一定要拎清，资源和计费的重要性不可不察，不然如果只关注算法而忽视其它，结局就是就是左右手互搏，但凡 trade-off 就会产生净损耗。

等当了经理后，我会穿上一双皮鞋的，或许会穿得像你这样，或许会更好些，我也不知道，到时候看吧，也可能更便宜。

浙江温州皮鞋湿，下雨进水不会胖。