递归的本质

一、算法描述
1.递归算法（recursion algorithm）
在计算机科学中是指一种通过重复将主问题分解为同类子问题而解决问题的方法。

2.递归的定义
在函数的定义中，其内部操作又直接或间接地出现对自身的调用。

递归的能力在于用有限的语句来定义对象的无限集合。递归算法只需少量的代码语句就可描述出解题过程所需要的多次重复计算，大大减少代码量。

例如，在数学上，所有偶数的集合可递归地定义为：

(1)
0
0 是一个偶数；

(2)一个偶数与 
2
2 的和是一个偶数。

仅需两句话就能定义一个由无穷多个元素组成的集合。

再如，阶乘的递归定义数学表达式：

f(0)=1

∀n>0,f(n)=n×f(n−1)

二、执行过程
递归，其包含了两个意思：递（去）、归。

 

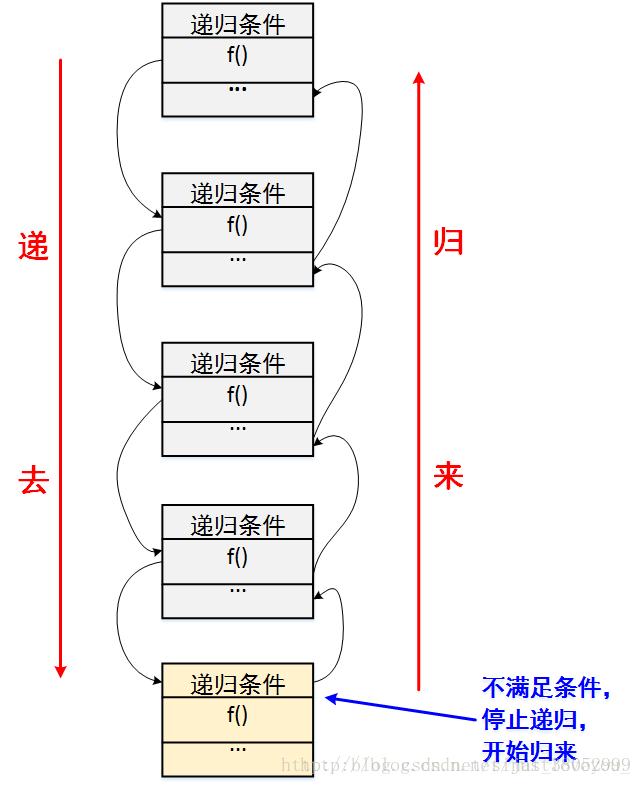
递归问题必须可以分解为若干个规模较小，与原问题形式相同的子问题，这些子问题可以用相同的解题思路来解决。

这些问题的演化过程是一个从大到小，由近及远的过程，并且会有一个明确的终点（临界点）。一旦到达了这个临界点，就不用再往更小、更远的地方走下去。最后，从这个临界点开始，原路返回到原点，原问题解决。

三、递归算法的使用条件
1.问题a可以转化为一个规模更小的新问题a1，但是新问题a1的解法必须和a相同（递归算法的核心思想）；

2.必须有明确的递归终止条件（递归边界）。

3.注意：理论上，能用循环解决的问题，都可以用递归解决，但是：

(1)递归的执行效率远远低于循环；

(2)递归的层数，受制于系统堆栈的大小（不同配置的机器默认大小不同），因此，不宜写递归调用层数太深的程序。

四、常用方法
1.直接递归
a( ){ a( ); }
2.间接递归
a( ){    b(); }
b( ){    a(); }