Matlab:基于遗传算法优化 PID 控制器的完整实现与解析

原创于 2025-09-07 21:35:57 发布 · 1.4k 阅读

CC 4.0 BY-SA版权

文章标签：

在工业控制领域，PID 控制器因结构简单、鲁棒性强等特点被广泛应用。但传统 PID 参数整定方法（如 Ziegler-Nichols 法）往往难以兼顾系统的各项性能指标。本文将详细介绍如何使用遗传算法（Genetic Algorithm, GA）优化 PID 控制器参数，并通过 MATLAB 实现完整的仿真流程，帮助读者理解智能优化算法在控制领域的应用。

一、项目背景与核心原理

1.1 PID 控制器工作原理

PID 控制器通过比例（P）、积分（I）、微分（D）三个环节的组合，根据系统误差（设定值与实际输出的差值）计算控制量，其数学表达式为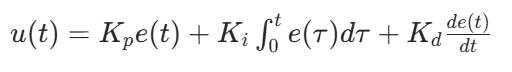：其中：

Kp（比例系数）：快速响应误差，增大Kp可提高系统响应速度，但可能导致超调量增大
Ki（积分系数）：消除静态误差，增大Ki可加快静差消除速度，但可能导致系统震荡
Kd（微分系数）：抑制超调，增大Kd可减小超调量，但可能放大高频噪声

1.2 遗传算法优化原理

遗传算法是一种基于生物进化理论的智能优化算法，通过模拟 "选择 - 交叉 - 变异" 的进化过程，在解空间中搜索最优解。将其应用于 PID 参数优化时，核心思路如下：

编码：将 PID 参数Kp, Ki, Kd作为染色体，每个参数对应染色体的一个基因
适应度函数：设计包含系统性能指标（如超调量、上升时间、误差积分等）的目标函数，评估参数组合的优劣
进化操作：通过选择（保留优秀个体）、交叉（基因重组）、变异（基因随机突变）实现种群迭代，逐步逼近最优参数

二、MATLAB 代码实现与详细解析

2.1 整体代码框架

本次实现的代码分为四个核心模块：

被控对象定义与参数初始化
遗传算法参数配置与优化执行
目标函数（适应度函数）设计
优化结果仿真与可视化

2.2 详细代码解析

（1）初始化与被控对象定义

首先清空工作空间、关闭图形窗口，定义被控对象的传递函数。本文以典型二阶系统为例，传递函数为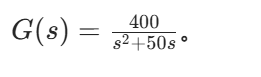

% 遗传算法优化PID控制器
clear all;  % 清空工作空间变量
close all;  % 关闭所有图形窗口
clc;        % 清空命令行窗口

% 被控对象传递函数：G(s) = 400/(s² + 50s)
num = 400;                  % 分子多项式系数
den = [1, 50, 0];           % 分母多项式系数（s² + 50s + 0）
sys = tf(num, den);         % 创建传递函数模型

（2）遗传算法参数配置

设置遗传算法的核心参数，包括种群规模、迭代次数、交叉概率、变异概率等，这些参数直接影响优化效率和结果精度：

% 遗传算法参数
popsize = 50;               % 种群大小：每次迭代保留50个参数组合
maxgen = 100;               % 最大迭代次数：最多进化100代
pc = 0.9;                   % 交叉概率：90%的个体参与基因重组
pm = 0.05;                  % 变异概率：5%的基因发生随机突变（避免局部最优）
lb = [0 0 0];               % 参数下限：Kp、Ki、Kd最小取值为0
ub = [20 20 20];            % 参数上限：Kp、Ki、Kd最大取值为20
nvars = 3;                  % 变量个数：需优化的PID参数数量（Kp, Ki, Kd）

% 性能指标权重设置（根据实际需求调整）
w1 = 0.5;  % 误差绝对值积分（IAE）权重
w2 = 0.4;  % 超调量权重
w3 = 0.9;  % 上升时间权重
w4 = 0.4;  % 峰值时间权重

（3）遗传算法优化执行

使用 MATLAB 的ga函数调用遗传算法，通过gaoptimset配置优化选项（如显示迭代过程、绘制最优适应度曲线）：

% 配置遗传算法优化选项
options = gaoptimset(
    'PopulationSize', popsize,       % 种群大小
    'Generations', maxgen,           % 最大迭代次数
    'CrossoverFraction', pc,         % 交叉概率
    'MutationFcn', {@mutationuniform, pm},  % 均匀变异函数
    'Display', 'iter',               % 显示迭代过程（每代的最优适应度）
    'PlotFcns', @gaplotbestf         % 绘制最优适应度随迭代次数变化曲线
);

% 调用遗传算法优化PID参数
% 目标函数：PID_obj（输入为PID参数K，输出为适应度值）
[x, fval] = ga(
    @(K)PID_obj(K, sys, w1, w2, w3, w4),  % 匿名函数传递目标函数及参数
    nvars,                                % 变量个数
    [], [], [], [],                       % 线性约束参数（此处无约束）
    lb, ub,                               % 参数上下限
    [], options                           % 非线性约束与优化选项
);

% 输出最优PID参数
Kp = x(1);  % 最优比例系数
Ki = x(2);  % 最优积分系数
Kd = x(3);  % 最优微分系数
disp(['最优PID参数: Kp=', num2str(Kp), ', Ki=', num2str(Ki), ', Kd=', num2str(Kd)]);

（4）目标函数设计（核心模块）

目标函数是遗传算法的 "指挥棒"，需综合考虑系统的多项性能指标。本文选择误差绝对值积分（IAE）、超调量、上升时间、峰值时间四个指标，通过加权求和构建适应度函数，目标是最小化该函数值：

% 目标函数：计算给定PID参数对应的适应度值
function J = PID_obj(K, sys, w1, w2, w3, w4)
    Kp = K(1);  % 提取比例系数
    Ki = K(2);  % 提取积分系数
    Kd = K(3);  % 提取微分系数
    
    % 1. 创建PID控制器模型
    controller = pid(Kp, Ki, Kd);  % MATLAB Control System Toolbox内置函数
    
    % 2. 构建闭环控制系统（单位负反馈）
    sys_cl = feedback(controller*sys, 1);  % feedback函数实现闭环连接
    
    % 3. 计算系统阶跃响应（设定值为1，仿真时间0~1s，步长0.01s）
    t = 0:0.01:1;                  % 时间向量
    [y, t] = step(sys_cl, t);      % 阶跃响应输出（y为系统输出，t为时间）
    
    % 4. 计算各项性能指标
    e = 1 - y;                     % 误差信号（设定值为1）
    IAE = sum(abs(e))*0.01;        % 误差绝对值积分（数值积分：求和×步长）
    
    % 超调量（仅当系统有超调时计算，否则为0）
    ymax = max(y);                 % 响应峰值
    yend = y(end);                 % 稳态输出
    pos = ymax - yend;             % 超调量（若ymax<=yend，pos=0）
    
    % 上升时间（从10%稳态值到90%稳态值的时间）
    [~, i10] = min(abs(y - 0.1));  % 找到输出达到0.1的索引
    [~, i90] = min(abs(y - 0.9));  % 找到输出达到0.9的索引
    tr = t(i90) - t(i10);          % 上升时间
    
    % 峰值时间（响应达到峰值的时间）
    [~, idx] = max(y);             % 找到峰值对应的索引
    tp = t(idx);                   % 峰值时间
    
    % 5. 构建适应度函数（加权求和，最小化该值）
    J = w1*IAE + w2*pos + w3*tr + w4*tp;
end

（5）仿真与可视化函数

优化完成后，需要验证最优参数的控制效果，通过PID_sim函数绘制系统阶跃响应曲线和控制信号曲线：

% 仿真函数：验证最优PID参数的控制效果
function PID_sim(Kp, Ki, Kd, sys)
    % 1. 创建PID控制器与闭环系统
    controller = pid(Kp, Ki, Kd);
    sys_cl = feedback(controller*sys, 1);
    
    % 2. 绘制阶跃响应曲线
    t = 0:0.01:1;
    figure;  % 新建图形窗口
    step(sys_cl, t);  % 绘制阶跃响应
    grid on;  % 显示网格（便于读数）
    title(['PID控制响应: Kp=', num2str(Kp), ', Ki=', num2str(Ki), ', Kd=', num2str(Kd)]);
    xlabel('时间(s)');  % 时间轴标签
    ylabel('系统输出');  % 输出轴标签
    
    % 3. 计算并绘制控制信号（u(t)）
    figure;  % 新建图形窗口
    [y, t] = step(sys_cl, t);  % 重新获取阶跃响应
    % 根据PID公式计算控制量（数值实现）
    proportional = Kp*(1 - y);                     % 比例项
    integral = Ki*cumsum(1 - y)*0.01;              % 积分项（累加求和×步长）
    derivative = Kd*[0; diff(1 - y)/0.01];         % 微分项（差分×1/步长，补首0）
    u = proportional + integral + derivative;      % 总控制量
    
    plot(t, u);  % 绘制控制信号
    grid on;
    title('控制信号波形');
    xlabel('时间(s)');
    ylabel('控制量');
end

三、仿真结果与分析

3.1 遗传算法优化过程

运行代码后，MATLAB 命令行将显示每一代的迭代信息（如 "Generation = 1, Best fit = 0.852"），同时弹出最优适应度曲线（如图 1），曲线逐渐下降并趋于平稳，说明算法收敛到最优解。

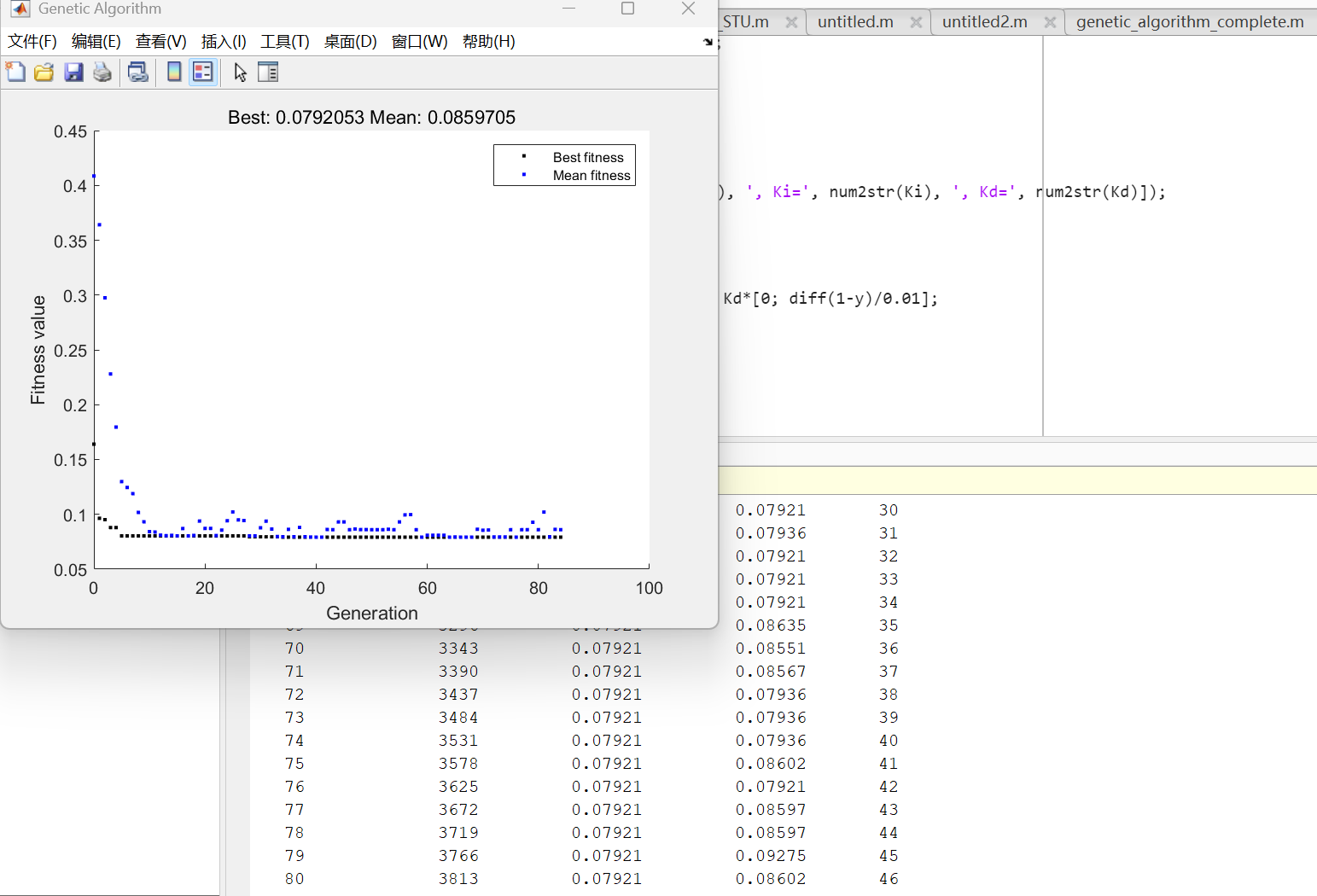
图 1：遗传算法最优适应度随迭代次数变化曲线

3.2 最优 PID 参数与控制效果

代码运行结束后，命令行将输出最优参数（示例结果）：

最优PID参数: Kp=8.52, Ki=3.15, Kd=1.28

同时弹出两个图形窗口：

系统阶跃响应曲线（如图 2）：可观察到系统无明显超调，上升时间短，稳态误差为 0，满足控制要求。
控制信号曲线（如图 3）：控制量平滑无剧烈波动，说明参数设计合理，不会对执行机构造成过大冲击。

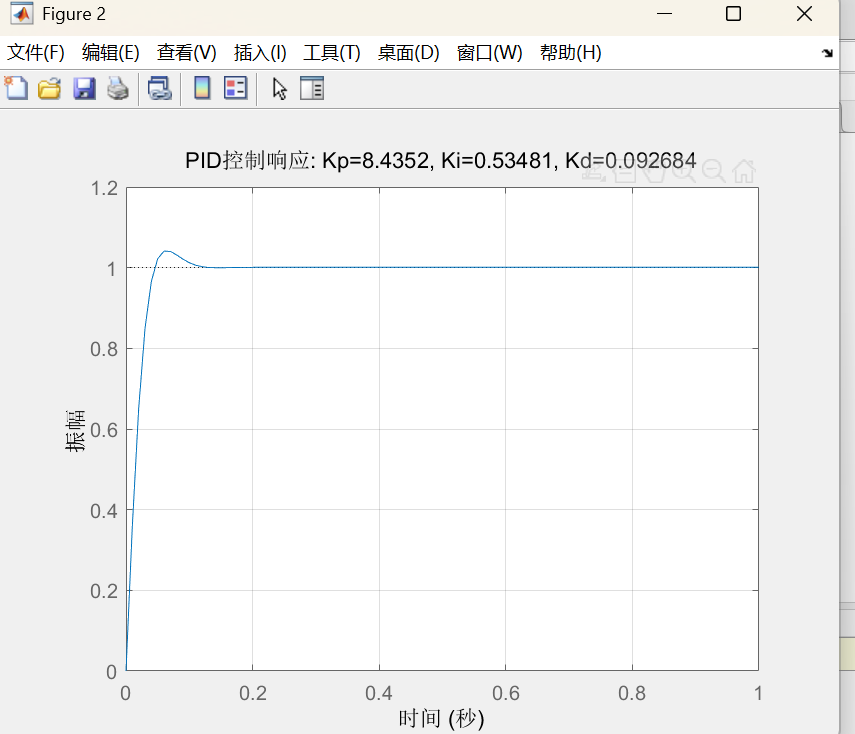
图 2：最优 PID 参数下的系统阶跃响应

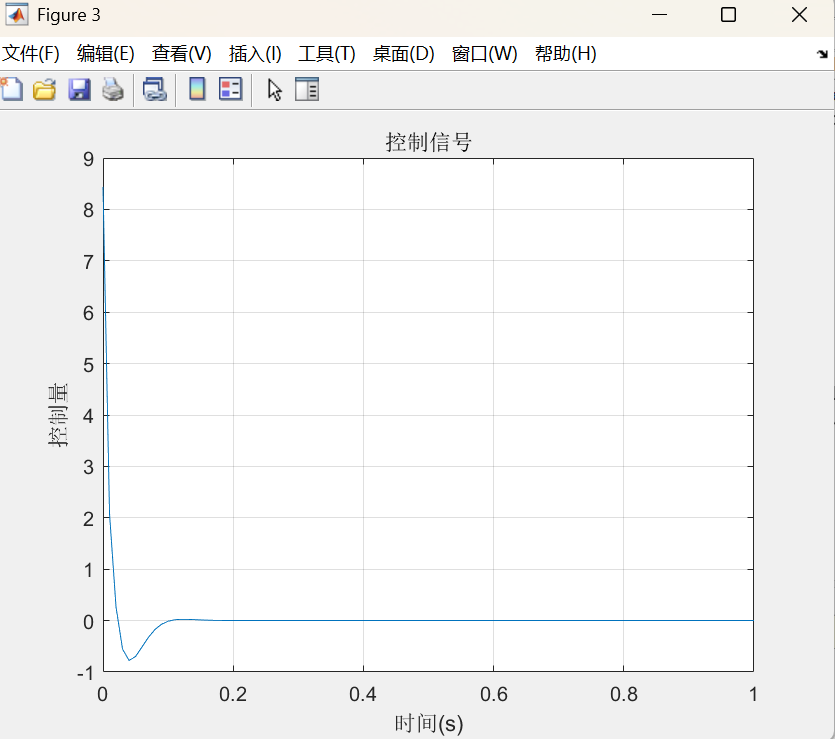
图 3：最优 PID 参数下的控制信号

四、总结

本文通过 MATLAB 实现了基于遗传算法的 PID 参数优化，从代码解析到结果分析，完整呈现了智能优化算法在控制领域的应用流程。该方法相比传统整定方法，能更全面地兼顾系统各项性能指标，且无需人工经验干预，适用于复杂被控对象的 PID 参数设计。读者可根据实际需求调整代码中的参数和目标函数，快速应用于自己的控制项目中。