codeforces1013D（模拟，并查集）

最新推荐文章于 2024-09-02 20:42:45 发布

原创最新推荐文章于 2024-09-02 20:42:45 发布 · 901 阅读

0 ·

CC 4.0 BY-SA版权

模拟专栏收录该内容

13 篇文章

订阅专栏

本文介绍了一种使用并查集数据结构解决n*m区域中所有格子被标记覆盖的算法。通过优化放置标记的位置，可以实现用最少的标记数达到完全覆盖的目标。文章详细解释了并查集的实现过程及如何利用它来减少重复标记，从而得到最优解。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

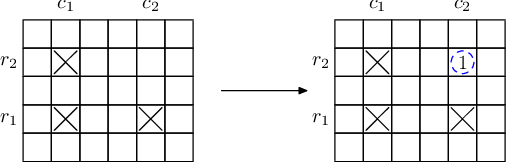
题目:给你n*m的区域，q个格子放上了标记，如上图放了(r1,c1),(r1,c2),(r2,c1)后(r2,c2)就可以自动出来标记，问让最后所有的格子都被标记还需要的最小标记数。

思路:假设没有一个格子放有标记。下图还需放n+m-1个标记，能把所有的格子标记完。此时是最优的

然后把q个多放的格子放进去等效替换就可以啦，并查集去重。

#include <bits/stdc++.h>
using namespace std;
const int maxn=4e5+100;
int n,m,q,fa[maxn];
int findfa(int x)
{
    if(x==fa[x])return x;
    int y=x,tmp;
    while(x!=fa[x]) x=fa[x];
    while(fa[y]!=x)
    {
        int tmp=fa[y];
        fa[y]=x;
        y=tmp;
    }
    return x;
}
int main()
{
    scanf("%d%d%d",&n,&m,&q);
    for(int i=1;i<=n+m;i++)
        fa[i]=i;
    int ans=n+m-1;
    while(q--)
    {
        int x,y,fx,fy;
        scanf("%d%d",&x,&y);
        y+=n;
        fx=findfa(x);
        fy=findfa(y);
        if(fx!=fy)
        {
            fa[fx]=fy;
            ans--;
        }
    }
    printf("%d\n",ans);
    return 0;
}