欧拉筛（线性筛）：找出所有小于等于给定整数n的质数的算法

大体思路：

        与埃氏筛不同，埃氏筛（Java）：找出所有小于等于给定整数n的质数的算法-优快云博客

        欧拉筛不是把素数的所有倍数标记为非素数，而是每扫过一个数(这个数用外循环的 i 来表示，遍历isPrime数组）（无论这个数是素数还是非素数）将该数与前面标记为素数的数相乘的数筛掉（内循环进行更新真正的质数primes质数列表）。

 确保每个合数仅被其最小质因数标记一次，这样才能解决重复标记问题，时间复杂度降为O(n)

欧拉筛的核心思想（两个表）

1.isPrime数组：用于标记每个数是否为素数。初始时所有数被假设为素数（true），之后通过标记合数为false来筛选出素数。

2.primes列表：存储已发现的素数。每次外层循环找到一个素数时，会将其加入列表，然后内层循环利用这个列表中的素数来生成合数并标记。

然后，要注意这两个表如何协同工作。例如，当处理数i时，如果i是素数，会被加入 primes 列表。接着，内层循环遍历 primes 中的每个素数p，计算 i*p ，并在 isPrime 中标记该乘积为合数。同时，通过 if (i % p == 0) break; 来确保每个合数只被其最小质因数标记一次，避免重复。

核心目标

        每个合数只被标记一次，且由它的最小质因数进行标记。

        例如：合数12应被标记为6*2（2是12的最小质因数），而非4*3。

实现原理

        写两个表，一个是初始全为素数（isprimes），一个是随时更新素数的表（primes列表）。

        维护一个素数列表primes，记录当前已知的所有素数。

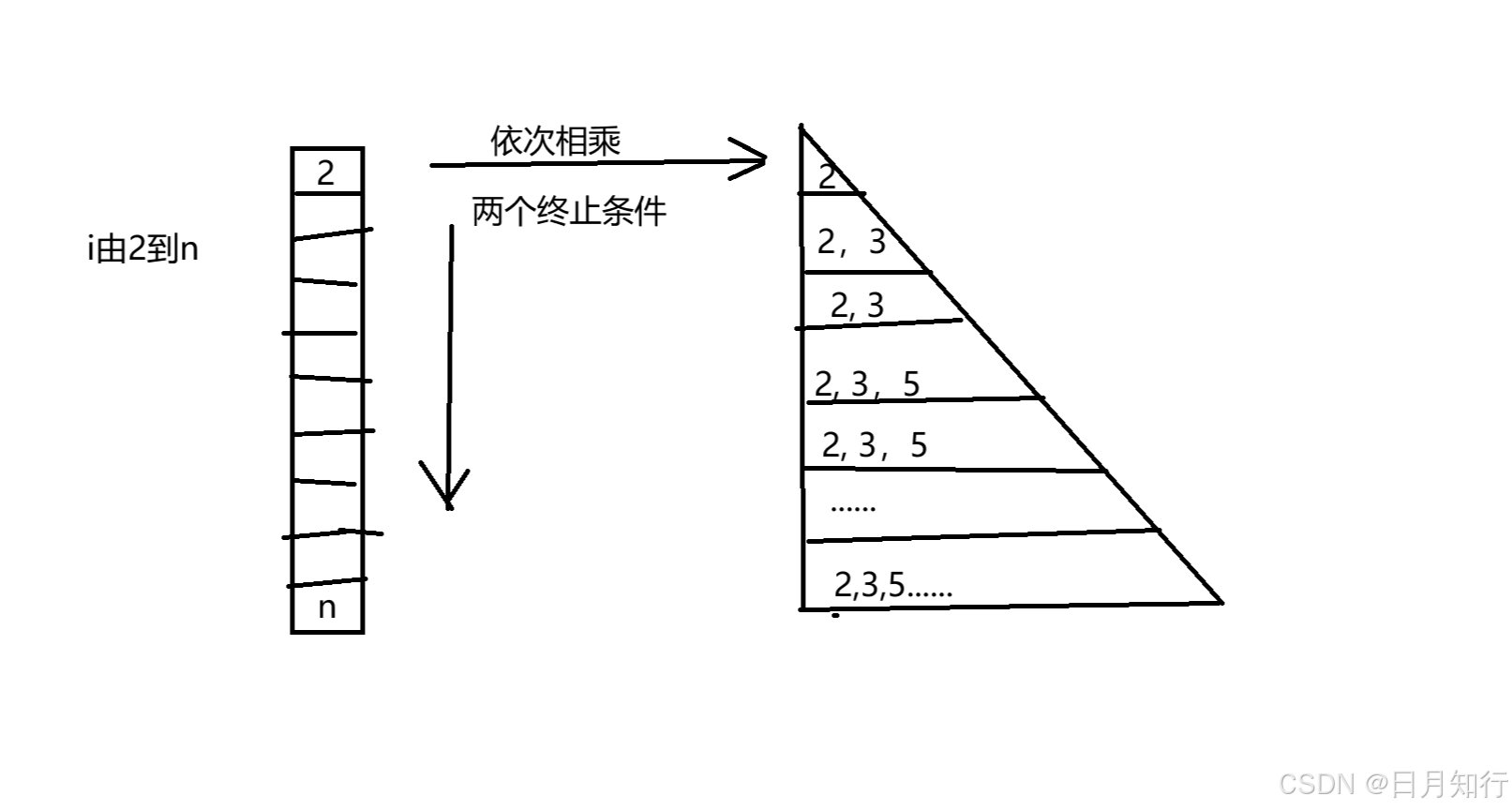
        对于每个数i（从2开始遍历到n）：

        如果i是素数，加入primes列表。用i与primes中的素数依次相乘，生成合数并标记，什么时候不能标记以免重复呢？要注意终止条件。

未注意终止条件前：

2*2

3*3 ,  3*3

4*2，4*3

5*2，5*3，5*5

6*2,   6*3,   6*5

......

当前i	素数列表（primes）
2	[2]
3	[2, 3]
4	[2, 3]
5	[2, 3, 5]
6	[2, 3, 5]

        两个终止条件：

终止条件1：超出范围  （即i*primes列表中的数不能超过给定的正整数n)

终止条件2：if (i % p == 0) break; （p为primes质数列表中的数）用这种方法来确保每个合数只被其最小质因数标记一次，避免重复

    if (product > n) break; // 终止条件1：超出范围
    isPrime[product] = false; // 标记合数
    if (i % p == 0) break; // 终止条件2：保证最小质因数标记

算法流程示例（以n=12为例）

当前i	素数列表（primes）	标记操作	终止条件
2	[2]	2*2=4 → 标记4	2%2=0 → 终止
3	[2, 3]	3*2=6 → 标记6；3*3=9 → 标记9	3%3=0 → 终止
4	[2, 3]	4*2=8 → 标记8	4%2=0 → 终止
5	[2, 3, 5]	5*2=10 → 标记10	5*3>12 → 终止
6	[2, 3, 5]	6*2=12 → 标记12	6%2=0 → 终止

剩下的7，8，9，10，11，12都因乘2后>12直接终止

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

public class EulerSieve {
    public static List<Integer> eulerSieve(int n) {
        boolean[] isPrime = new boolean[n + 1];
        Arrays.fill(isPrime, true); // 初始假设所有数都是素数
        List<Integer> primes = new ArrayList<>();
        
        for (int i = 2; i <= n; i++) {
            if (isPrime[i]) {
                primes.add(i); // 将i标记为素数
            }
            // 用当前i与已知素数生成合数
            for (int j = 0; j < primes.size(); j++) {
                int p = primes.get(j);
                int product = i * p;
                if (product > n) break; // 超出范围则终止
                isPrime[product] = false; // 标记i*p为合数
                if (i % p == 0) break; // 关键终止条件
            }
        }
        return primes;
    }

    public static void main(String[] args) {
        int n = 30;
        List<Integer> primes = eulerSieve(n);
        System.out.println("素数列表（≤" + n + "）：" + primes);
    }
}

记忆窍门：

依次乘三角，别忘终止条件