【hiho一下第77周】递归-减而治之 (MS面试题：Koch Snowflake)

最新推荐文章于 2018-11-26 17:38:56 发布

转载最新推荐文章于 2018-11-26 17:38:56 发布 · 154 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/Inkblots/p/5062341.html

本文详细解析了Koch雪花曲线的生成算法，通过递归方式解决微软面试题，探讨了如何计算特定边在迭代过程中的生成代数。文章提供了具体代码实现，帮助读者理解并掌握这一经典的分形几何问题。

本题是一道微软面试题，看起来复杂，解出来会发现其实是一个很简单的递归问题，但是这道题的递归思路是很值得我们反复推敲的。

原题为hihocoder第77周的题目。

描述

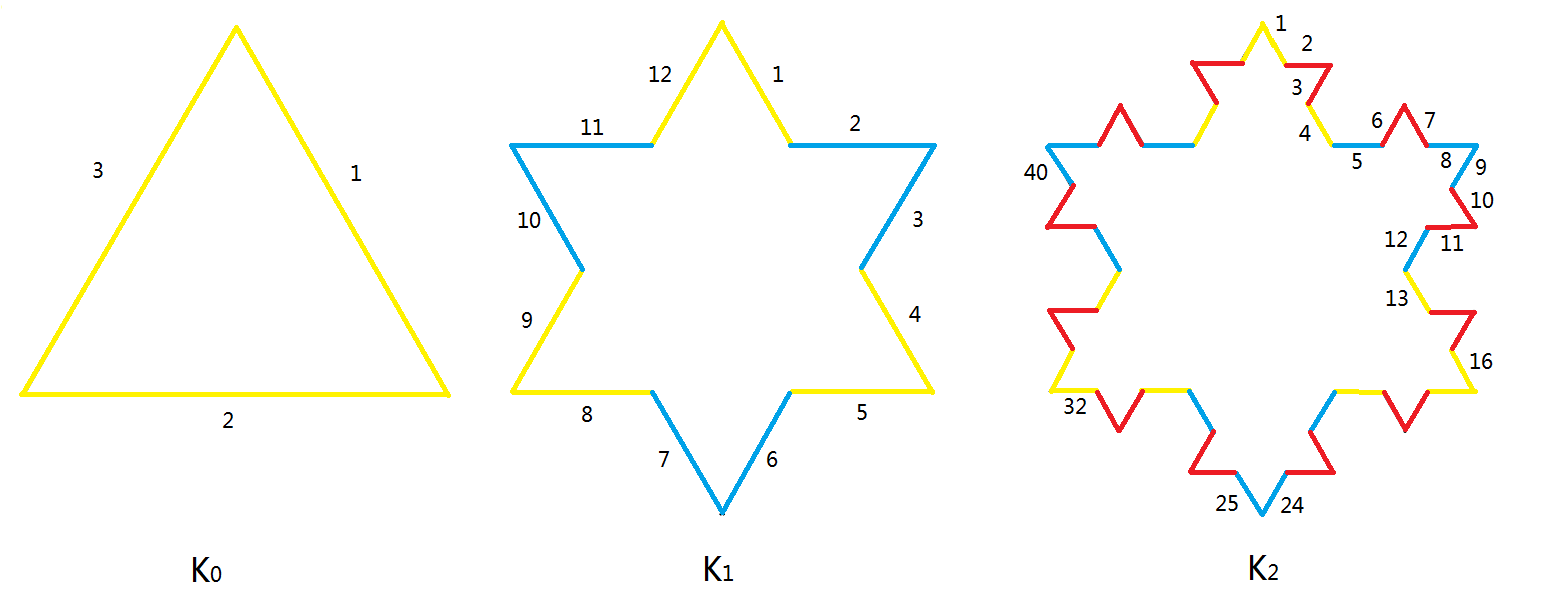
Koch Snowflake is one of the most famous factal. It is built by starting with an equilateral triangle, removing the inner third of each side, building another equilateral triangle at the location where the side was removed, and then repeating the process indefinitely.

Let K_n be the Koch Snowflake after n-th iteration. It is obvious that the number of sides of K_n, N_n, is 3*4ⁿ. Let's number the sides clockwisely from the top of Koch Snowflake.

Let s_i,n be the i-th side of K_n. The generation of s_i,n is defined as the smallest m satifying s_i,n is a part of the sides of K_m. For example, in the above picture, the yellow sides are of generation 0; the blue sides are of generation 1; the red sides are of generation 2.

Given a side s_i,n, your task is to calculate its generation.

输入

The input contains several test cases.

The first line contains T(T <= 1000), the number of the test cases.

The following T lines each contain two numbers, i(1 <= i <= 10^9) and n(0 <= n <= 1000). Your task is to calculate the generation of side s_i,n.

输出

For each test case output the generation of the side.

样例输入

样例输出

题目大意：

　　给定一个三角形，每经过一次扩展，每一条边变成4条小边。告诉你扩展的次数n，以及边的编号i，求该条边是第几次扩展出现的边。

题目思路：

　　这道题初看是令人有点头疼的数学问题，需要找数字之间的规律，如果单看每一次扩展，找规律就会显得非常复杂，要让解题过程简单化，就应该从一条边看起。

　　我用hihocoder上题目分析的图片来解释会更加直观，例如第i条边经过扩展后：

　　也就是说中间两条边是经过第n次扩展后得到的，而左右两边则不能够确定。

　　左右两边经过规律的反推可以继续找这条件是否属于第n-1次扩展，否则继续减而治之。

　　具体代码如下：

 1 //递归(减而治之)-单边分析
 2 //第i条边经扩展后的四边编号
 3 //i->4 * (i - 1) + 1, 4 * (i - 1) + 2, 4 * (i - 1) + 3, 4 * (i - 1) + 4
 4 //Time:0Ms Memory:0K
 5 #include<iostream>
 6 #include<cstdio>
 7 using namespace std;
 8 
 9 int cal(int side, int n)
10 {
11     if (n == 0)
12         return 0;
13     if (side % 4 == 2 || side % 4 == 3)    //如果边模4为2或3 则确定为n次扩展出的边
14         return n;
15     else                                //否则 减小一个规模continue
16         return cal((side + 3) / 4, n - 1);    //降低的边数 经归纳可等价 (side + 3)/4
17 }
18 
19 int main()
20 {
21     int T;
22     scanf("%d", &T);
23     while (T--)
24     {
25         int side, n;
26         scanf("%d%d", &side, &n);
27         printf("%d\n", cal(side, n));
28     }
29 
30     return 0;
31 }

转载于:https://www.cnblogs.com/Inkblots/p/5062341.html