[SCOI2005] 扫雷 题解

题面：[SCOI2005] 扫雷

题目描述

相信大家都玩过扫雷的游戏。那是在一个$n\times m$的矩阵里面有一些雷，要你根据一些信息找出雷来。万圣节到了，“余”人国流行起了一种简单的扫雷游戏，这个游戏规则和扫雷一样，如果某个格子没有雷，那么它里面的数字表示和它8连通的格子里面雷的数目。现在棋盘是$n\times 2$的，第一列里面某些格子是雷，而第二列没有雷，如下图：

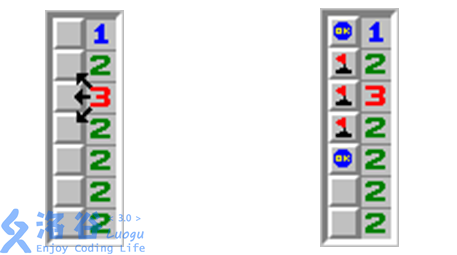
由于第一列的雷可能有多种方案满足第二列的数的限制，你的任务即根据第二列的信息确定第一列雷有多少种摆放方案。

输入格式

第一行为N，第二行有N个数，依次为第二列的格子中的数。（1<= N <= 10000）

输出格式

一个数，即第一列中雷的摆放方案数。

样例 #1

样例输入 #1

2
1  1

样例输出 #1

2

做法1 状压dp，$O(n)$，100pts

看到这个方案数，第一反应$dp$。

设$d{p}_{i,j}(i\in [1,n],j\in [0,7])$表示对于第$i$格范扫描范围内（即$i-1\sim i+1$三行，$n+1$视为没有雷即可）雷的排列方式为$j$（的二进制表示）的可能数量。

通过观察得到一个情况可以由上一个情况递推得到，当且仅当当前状况的后两位等于上一个状况的前两位，于是可以获得上图最后一行写的信息。

但是在递推的时候应当注意若排列方式与当前格的雷数量不符，应设为$0$。

特别的，初始值应当为$d{p}_{0,0}=1，d{p}_{0,4}=1$

到这里就可以AC了……吗？

#include<iostream>
#include<algorithm>
#include<cstring>

using namespace std;

const int N=1e4+10;
const int c[8]={0,1,1,2,1,2,2,3};
const int last[8]={0,2,4,6,0,2,4,6};

int n;
int a[N],dp[N][8];

int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
		cin>>a[i];
	dp[0][0]=1;
	dp[0][4]=1;
	for(int i=1;i<=n;i++)
		for(int j=0;j<8;j++)
			if(c[j]==a[i])
				dp[i][j]+=dp[i-1][last[j]]+dp[i-1][last[j]+1];
	int res=0;
	for(int i=0;i<8;i++)
		res+=dp[n][i];
	cout<<res<<endl;
	return 0;
}

（AC人可以不用看了,如果你90pts WA on #8，往下看）

---

好像还有点问题……

read 1,expect 0没有任何价值，分析之前的定义和思路，好像没问题啊？

但是，在一个不起眼的括号里，有这么一句话：n+1视为没有雷即可。

因此代码中当$i=n$时，应当由$j<4$，而不是$j<8$。

修改后AC。

#include<iostream>
#include<algorithm>
#include<cstring>

using namespace std;

const int N=1e4+10;
const int c[8]={0,1,1,2,1,2,2,3};
const int last[8]={0,2,4,6,0,2,4,6};

int n;
int a[N],dp[N][8];

int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
		cin>>a[i];
	dp[0][0]=1;
	dp[0][4]=1;
	for(int i=1;i<=n;i++)
		for(int j=0;j<(i==n?4:8);j++)
			if(c[j]==a[i])
				dp[i][j]+=dp[i-1][last[j]]+dp[i-1][last[j]+1];
	int res=0;
	for(int i=0;i<8;i++)
		res+=dp[n][i];
	cout<<res<<endl;
	return 0;
}

做法2 递推，O(n)，100pts

作为一个考试时写完会做的就开始扫雷的人，看到题目就发现，当第一个点确定有/没有雷后，接下来一排都可以确定了。（停下来，想一下为什么？）

于是我们只需要设第一行有/没有雷分别跑一遍递推看是否成立即可。

y1s1，这样显得我一个写状压的人像个小丑。

#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;

const int N=1e4+10;

int n;
int a[N];

int dfs(int p1,int p2,int x)
{
	if(x==n+1)
		return p2==0;
	int k=a[x];
	k-=p1;
	k-=p2;
	if(k<0)
		return 0;
	return dfs(p2,k,x+1);
}

int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
		cin>>a[i];
	int res=0;
	res+=dfs(0,0,1);
	res+=dfs(0,1,1);
	cout<<res;
	return 0;
}