P5658 [CSP-S2019] 括号树

题面

题目背景

本题中合法括号串的定义如下：

1. () 是合法括号串。
2. 如果 A 是合法括号串，则 (A) 是合法括号串。
3. 如果 A，B 是合法括号串，则 AB 是合法括号串。

本题中子串与不同的子串的定义如下：

1. 字符串 S 的子串是 S 中连续的任意个字符组成的字符串。S 的子串可用起始位置 $l$ 与终止位置 $r$ 来表示，记为 $S(l,r)$（$1\le l\le r\le |S|$，$|S|$ 表示 S 的长度）。
2. S 的两个子串视作不同当且仅当它们在 S 中的位置不同，即 $l$ 不同或 $r$ 不同。

题目描述

一个大小为 $n$ 的树包含 $n$ 个结点和 $n-1$ 条边，每条边连接两个结点，且任意两个结点间有且仅有一条简单路径互相可达。

小 Q 是一个充满好奇心的小朋友，有一天他在上学的路上碰见了一个大小为 $n$ 的树，树上结点从 $1\sim n$ 编号，$1$ 号结点为树的根。除 $1$ 号结点外，每个结点有一个父亲结点，$u$（$2\le u\le n$）号结点的父亲为 $f_u$（$1\le f_u<u$）号结点。

小 Q 发现这个树的每个结点上恰有一个括号，可能是( 或)。小 Q 定义 $s_i$ 为：将根结点到 $i$ 号结点的简单路径上的括号，按结点经过顺序依次排列组成的字符串。

显然 $s_i$ 是个括号串，但不一定是合法括号串，因此现在小 Q 想对所有的 $i$（$1\le i\le n$）求出，$s_i$ 中有多少个互不相同的子串是合法括号串。

这个问题难倒了小 Q，他只好向你求助。设 $s_i$ 共有 $k_i$ 个不同子串是合法括号串， 你只需要告诉小 Q 所有 $i\times k_i$ 的异或和，即：
$$(1\times k_1)\text{xor}(2\times k_2)\text{xor}(3\times k_3)\text{xor}\cdots \text{xor}(n\times k_n)$$
其中 $xor$ 是位异或运算。

输入格式

第一行一个整数 $n$，表示树的大小。

第二行一个长为 $n$ 的由( 与) 组成的括号串，第 $i$ 个括号表示 $i$ 号结点上的括号。

第三行包含 $n-1$ 个整数，第 $i$（$1\le i<n$）个整数表示 $i+1$ 号结点的父亲编号 $f_{i+1}$。

输出格式

仅一行一个整数表示答案。

样例 #1

样例输入 #1

5
(()()
1 1 2 2

样例输出 #1

6

提示

【样例解释1】

树的形态如下图：

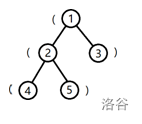
将根到 1 号结点的简单路径上的括号，按经过顺序排列所组成的字符串为 (，子串是合法括号串的个数为 $0$。

将根到 2 号结点的字符串为 ((，子串是合法括号串的个数为 $0$。

将根到 3 号结点的字符串为 ()，子串是合法括号串的个数为 $1$。

将根到 4 号结点的字符串为 (((，子串是合法括号串的个数为 $0$。

将根到 5 号结点的字符串为 (()，子串是合法括号串的个数为 $1$。

【数据范围】

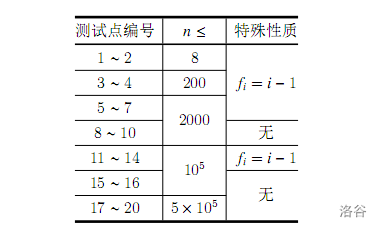
第一轮尝试 最淳朴的暴力 53pts

暴力求每一个字符串的子串个数，显然遍历结点有 $O(N)$ ，遍历子串 $O(N^2)$ ，单次查询 $O(N)$ ，共 $O(N^4)$ ，预期最差能过 $1\sim 4$ 号测试点（$N\le 200$）

test1.cpp

#include<iostream>
#include<algorithm>
#include<cstring>

using namespace std;

const int N=5e5+10;

int n;
int h[N],e[N<<1],ne[N<<1],idx;
int res;
string str;

void add(int a,int b)
{
	e[idx]=b;
	ne[idx]=h[a];
	h[a]=idx;
	idx++;
}

bool check(string s,int a,int b)
{
	int cnt=0;
	a--;
	b--;
	for(int i=a;i<=b;i++)
	{
		if(s[i]=='(')
			cnt++;
		else
		{
			if(cnt)
				cnt--;
			else
				return false;
		}
	}
	return cnt==0;
}

int count(string s)
{
	int cnt=0;
	for(int len=2;len<=s.size();len++)
		for(int i=1;i+len-1<=s.size();i++)
			if(check(s,i,i+len-1))
				cnt++;
	return cnt;
}

void dfs(int fa,int u,string s)
{
	s+=str[u-1];
	res^=u*count(s);
	for(int i=h[u];i!=-1;i=ne[i])
		if(e[i]!=fa)
			dfs(u,e[i],s);
	return;
}

int main()
{
	memset(h,-1,sizeof(h));
	cin>>n>>str;
	for(int i=2;i<=n;i++)
	{
		int a;
		cin>>a;
		add(a,i);
		add(i,a);
	}
	dfs(0,1,"");
	cout<<res<<endl;
	return 0;
}

但是因为数据没顶满，所以 $AC$ on #1 #2 #3 #4 #8 #9 #10，35 $pts$

第二轮尝试 特殊数据 70pts

分析数据的特殊性质，$$f_i=i-1$$ 等价于整棵树退化为链，问题转化为对于 $i$，求前 $i$ 位字符串的合法子串数。

观察到 $N\le 5\ast 10^5$，单次查询大概率为 $O(1)$ 或 $O(logn)$ 。显然从前往后遍历，很像线性 $dp$ 的逻辑，于是定义 $d{p}_i$ 为以 $i$ 结尾的合法子串的数量，则所求的结果 $re{s}_i$ 恰好为 $d{p}_{1\sim i}$ 的前缀和。并手动计算几组数据，看不同情况对于 $d{p}_i$ 的贡献。

数据 $1$（独立合法括号）：())()( $dp=[0,1,0,0,1,0]$ $res=[0,1,1,1,2,2]$

发现对于一个独立存在的合法括号串，对 $d{p}_i$ 的贡献为 $1$，这个很好找，只需要一个栈就可以。

数据 $2$（嵌套不相邻）：(())(((())) $dp=[0,0,1,1,0,0,0,0,1,1,1]$ $res=[0,,0,1,2,2,2,2,2,3,4,5]$

显然对于嵌套的括号，栈判断且贡献为 $1$ 仍成立，因为嵌套合法括号串在固定最后一个字符后无法拆分

数据 $3$（相邻不嵌套）：()())()()() $dp=[0,1,0,2,0,0,1,0,2,0,3]$ $res=[0,1,1,3,3,3,4,4,6,6,9]$

发现这次有一个后括号产生了大于 $1$ 的贡献，且第 $i$ 个的贡献为 $d{p}_{i-2}+1(i\ge 3)$

数据 $4$（嵌套且相邻）：()(()))() $dp[0,1,0,0,1,2,0,0,1]$ $res=[0,1,1,1,2,4,4,4,5]$

观察到此时上面的贡献计算公式不管用，但究其本质是一样的，即贡献为当前匹配的无相邻组合的合法括号串的前一位的贡献 $+1$。

以本组数据举例，根据上述定义为当前匹配的无相邻组合的合法括号串的前一位，计算 $pre=[0,1,2,3,3,2,6,6]$ 。

定义 $chec{k}_i=True$表示 $i$ 是否匹配，若 $i$ 匹配，与其匹配的字符是第 $k_i$ 个，则得出递推式 $$pr{e}_i=\{\begin{array}{rcl}i-1& & chec{k}_i=False\\ pr{e}_{k_i}& & chec{k}_i=True\end{array}$$

显然只要存栈的时候存的是编号，那么 $k_i$ 就可以直接得到。

代码呼之欲出，但是记得在暴力的基础上加特判，保留暴力分。同时上面过不了大数据所以没有开的 $longlong$也要开了

test2.cpp

#include<iostream>
#include<algorithm>
#include<cstring>
#include<stack>

using namespace std;

const int N=5e5+10;

int n;
int h[N],e[N<<1],ne[N<<1],idx;
int pre[N],dp[N];
long long ans[N];
long long res;
bool flag=1; 
string str;

void add(int a,int b)
{
	e[idx]=b;
	ne[idx]=h[a];
	h[a]=idx;
	idx++;
}

bool check(string s,int a,int b)
{
	int cnt=0;
	a--;
	b--;
	for(int i=a;i<=b;i++)
	{
		if(s[i]=='(')
			cnt++;
		else
		{
			if(cnt)
				cnt--;
			else
				return false;
		}
	}
	return cnt==0;
}

int count(string s)
{
	int cnt=0;
	for(int len=2;len<=s.size();len++)
		for(int i=1;i+len-1<=s.size();i++)
			if(check(s,i,i+len-1))
				cnt++;
	return cnt;
}

void dfs(int fa,int u,string s)
{
	s+=str[u-1];
	res^=u*count(s);
	for(int i=h[u];i!=-1;i=ne[i])
		if(e[i]!=fa)
			dfs(u,e[i],s);
	return;
}

void DP()
{
	stack<int> s;
	for(int i=1;i<=n;i++)
	{
		pre[i]=i-1;
		if(str[i-1]==')'&&!s.empty())
		{
			int t=s.top();
			s.pop();
			dp[i]=dp[pre[t]]+1;
		}
		else if(str[i-1]=='(')
			s.push(i);
		ans[i]=ans[i-1]+dp[i];
		res^=i*ans[i];
	}
	return;
}

int main()
{
	memset(h,-1,sizeof(h));
	cin>>n>>str;
	for(int i=2;i<=n;i++)
	{
		int a;
		cin>>a;
		if(a!=i-1)
			flag=0;
		add(a,i);
		add(i,a);
	}
	if(!flag)
		dfs(0,1,"");
	else
		DP();
	cout<<res<<endl;
	return 0;
}

结果就是 $TLE$ on #15-#20，即$10^5$ 以上的普通数据。

冲击满分 100pts

注意到刚刚的链上计算可以同样适用于树，于是将顺序遍历改为$dfs$，并且递归后恢复栈即可。

test3.cpp

#include<iostream>
#include<algorithm>
#include<cstring>

using namespace std;

const int N=5e5+10;

int n;
int h[N],e[N<<1],ne[N<<1],idx;
int pre[N],dp[N],s[N],top;
long long cnt[N],res;
string str;

void add(int a,int b)
{
	e[idx]=b;
	ne[idx]=h[a];
	h[a]=idx;
	idx++;
	return;
}

void dfs(int u,int fa)
{
	pre[u]=fa;
	if(str[u-1]=='(')
	{
		s[++top]=u;
		cnt[u]=cnt[fa]+dp[u];
		for(int i=h[u];i!=-1;i=ne[i])
		{
			int j=e[i];
			if(j!=fa)
				dfs(j,u);
		}
		top--;
	}
	else if(top>0&&str[u-1]==')')
	{
		int t=s[top];
		top--;
		dp[u]=dp[pre[t]]+1;
		cnt[u]=cnt[fa]+dp[u];
		for(int i=h[u];i!=-1;i=ne[i])
		{
			int j=e[i];
			if(j!=fa)
				dfs(j,u);
		}
		s[++top]=t;
	}
	else
	{
		cnt[u]=cnt[fa]+dp[u];
		for(int i=h[u];i!=-1;i=ne[i])
		{
			int j=e[i];
			if(j!=fa)
				dfs(j,u);
		}
	}
	res^=u*cnt[u];
	return;
}

int main()
{
	memset(h,-1,sizeof(h));
	cin>>n>>str;
	for(int i=2;i<=n;i++)
	{
		int a;
		cin>>a;
		add(a,i);
		add(i,a);
	}
	dfs(1,0);
	cout<<res;
	return 0;
}

愉快 $AC$