OpenCV SIFT算法原理详解及代码实现

 

1.尺度变换

目录

 

1.尺度变换

2.高斯差分金字塔

---

目的：构建尺度空间的目的就是找到在尺度变化中具有不变性的位置，可以使用连续的尺度变化，即在尺度空间中所有可能的尺度变化中找到稳定的特征点，通过这种方式找到的极点可以保证在图像缩放和旋转变化中具有不变性。

1.1相同大小的图像，利用高斯滤波，使图像进行不同尺度的模糊，（比如：可以得到4个不同程度模糊的相同尺寸图片）。

尺度空间内核是高斯函数。因此假设I(x,y)是原始图像，G(x,y,σ)是尺度空间可变的高斯函数

控制模糊程度，理解为标准差，图像变换越大，与原图像差值越大，即 越大越模糊。

2.在不同的分辨率的图像都要指定不同高斯滤波的结果，如下图右侧每层就做了五个高斯滤波：

2.高斯差分金字塔（DOG）

目的：高斯差分可以在尺度空间中找到稳定不变的极值点

如图：每一层有五个不同的高斯滤波模糊结果，差分得到四个差异性结果，极值较大的为较重要的点

定义：

其中kσ和σ是连续的两个图像的平滑尺度，其实就是 相同位置（x，y代表坐标位置）, 不同模糊程度的 两张图片进行 差分。

 

 

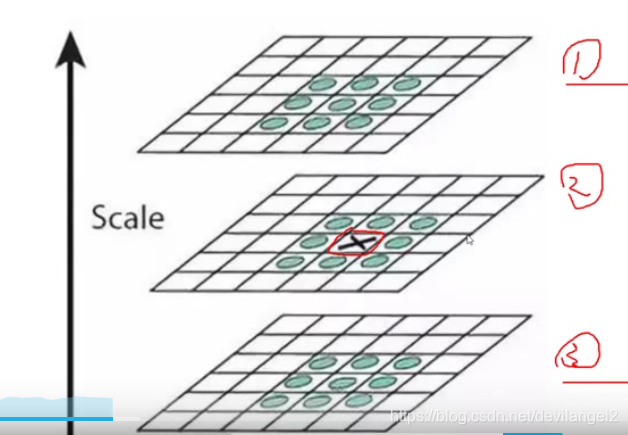
想寻找一个极值，要与周围 的点进行比较，要比较周围（上下层及周围点）共26个点。所以本 例产生的4个不同模糊，只有两个模糊可以进行比较（4-2）。可以得到不同极值点（离散）.

3.特征点的精确定位

目的：

计算机中存储的图像数据是离散的，而我们之前找到的极值点也就是离散空间中的极值点，但是离散空间中的极值点并不是真实的连续空间中的极值点