代码随想录 | 回溯算法总结

在代码随想录算法 | 回溯算法先导知识 | 题目分类，理论基础-优快云博客中我们详细的介绍了回溯算法的理论知识，不同于教科书般的讲解，这里介绍的回溯法的效率，解决的问题以及模板都是在刷题的过程中非常实用！

回溯是递归的副产品，只要有递归就会有回溯，所以回溯法也经常和二叉树遍历，深度优先搜索混在一起，因为这两种方式都是用了递归。

回溯法就是暴力搜索，并不是什么高效的算法，最多再剪枝一下。

回溯算法能解决如下问题：

• 组合问题：N个数里面按一定规则找出k个数的集合
• 排列问题：N个数按一定规则全排列，有几种排列方式
• 切割问题：一个字符串按一定规则有几种切割方式
• 子集问题：一个N个数的集合里有多少符合条件的子集
• 棋盘问题：N皇后，解数独等等

回溯法确实不好理解，所以需要把回溯法抽象为一个图形来理解就容易多了。

在代码随想录算法 | 回溯算法先导知识 | 题目分类，理论基础-优快云博客还用了回溯三部曲来分析回溯算法，并给出了回溯法的模板：

public void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

事实证明这个模板也伴随了整个回溯！

组合问题

组合问题

用回溯法解决第一道题目：组合问题。

代码随想录算法day19 | 回溯算法part01 | 77. 组合，216.组合总和III，17.电话号码的字母组合-优快云博客

我在文中开始的时候给大家列举k层for循环例子，进而得出都是同样是暴力解法，为什么要用回溯法！

此时大家应该深有体会回溯法的魅力，用递归控制for循环嵌套的数量！

博客中把回溯问题抽象为树形结构，如题：

可以直观的看出其搜索的过程：for循环横向遍历，递归纵向遍历，回溯不断调整结果集，这个理念贯穿整个回溯法系列。

对于回溯法的整体框架，网上搜的文章这块都说不清楚，按照天上掉下来的代码对着讲解，不知道究竟是怎么来的，也不知道为什么要这么写。

优化回溯算法只有剪枝一种方法，在很多题目中都把回溯法代码做了剪枝优化，举例第 77.组合 的树形结构如图：

大家可以一目了然剪的究竟是哪里。

剪枝精髓是：for循环在寻找起点的时候要有一个范围，如果这个起点到集合终止之间的元素已经不够题目要求的k个元素了，就没有必要搜索了。

在for循环上做剪枝操作是回溯法剪枝的常见套路！ 后面的题目还会经常用到。

组合总和

组合总和（一）

在代码随想录算法day20 | 回溯算法part02 | 39. 组合总和，40.组合总和II，131.分割回文串-优快云博客中，相当于 代码随想录算法day19 | 回溯算法part01 | 77. 组合，216.组合总和III，17.电话号码的字母组合-优快云博客加了一个元素总和的限制。

树形结构如图： 

整体思路还是一样的，本题的剪枝会好想一些，即：已选元素总和如果已经大于n（题中要求的和）了，那么往后遍历就没有意义了，直接剪掉，如图：

在本题中，依然还可以有一个剪枝，就是对for循环选择的起始范围的剪枝。

所以剪枝的代码可以在for循环加上 i <= 9 - (k - path.size()) + 1 的限制！

组合总和（二）

在 39.组合总和 中讲解的组合总和问题，和 77.组合 和 216.组合总和Ⅲ 的区别是：本题没有数量要求，可以无限重复，但是有总和的限制，所以间接的也是有个数的限制。

不少同学都是看到可以重复选择，就义无反顾的把startIndex去掉了。

本题还需要startIndex来控制for循环的起始位置，对于组合问题，什么时候需要startIndex呢？

我举过例子，如果是一个集合来求组合的话，就需要startIndex，例如：​​​​​​​77.组合 和 216.组合总和Ⅲ。

如果是多个集合取组合，各个集合之间相互不影响，那么就不用startIndex，例如：17.电话号码的字母组合

注意以上我只是说求组合的情况，如果是排列问题，又是另一套分析的套路。

树形结构如下： 

最后还给出了本题的剪枝优化，如下：

for (int i = startIndex; i < candidates.length && sum + candidates[i] <= target; i++)

优化后树形结构如下：

组合总和（三）

在 40.组合总和Ⅲ 中集合元素会有重复，但要求解集不能包含重复的组合。

所以难就难在去重问题上了。

这个去重问题，大家都知道有多么的晦涩难懂。网上的题解一般就说“去掉重复”，但说不清怎么个去重，代码一甩就完事了。

都知道组合问题可以抽象为树形结构，那么“使用过”在这个树形结构上是有两个维度的，一个维度是同一树枝上“使用过”，一个维度是同一树层上“使用过”。没有理解这两个层面上的“使用过” 是造成大家没有彻底理解去重的根本原因。

我在图中将used的变化用橘黄色标注上，可以看出在candidates[i] == candidates[i - 1]相同的情况下：

• used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
• used[i - 1] == false，说明同一树层candidates[i - 1]使用过

这块去重的逻辑很抽象，网上搜的题解基本没有能讲清楚的，如果大家之前思考过这个问题或者刷过这道题目，看到这里一定会感觉通透了很多！

对于去重，其实排列和子集问题也是一样的道理。

个集合求组合

在 17.电话号码的字母组合 中，开始用多个集合来求组合，还是熟悉的模板题目，但是有一些细节。

例如这里for循环，可不像是在 ​​​​​​​77.组合 和 216.组合总和Ⅲ 中从startIndex开始遍历的。

因为本题每一个数字代表的是不同集合，也就是求不同集合之间的组合，而 ​​​​​​​77.组合 和 216.组合总和Ⅲ 都是是求同一个集合中的组合！

树形结构如下：

如果大家在现场面试的时候，一定要注意各种输入异常的情况，例如本题输入1 * #按键。

其实本题不算难，但也处处是细节，还是要反复琢磨。

切割问题

在 131.切割回文串 中，文章开始讲解切割问题，虽然最后代码看起来好像是一道模板题，但是从分析到学会套用这个模板，是比较难的。

代码随想录算法day20 | 回溯算法part02 | 39. 组合总和，40.组合总和II，131.分割回文串-优快云博客

下面列出如下几个难点：

• 切割问题其实类似组合问题
• 如何模拟那些切割线
• 切割问题中递归如何终止
• 在递归循环中如何截取子串
• 如何判断回文

如果想到了用求解组合问题的思路来解决 切割问题本题就成功一大半了，接下来就可以对着模板照葫芦画瓢。

但后序如何模拟切割线，如何终止，如何截取子串，其实都不好想，最后判断回文算是最简单的了。

所以本题应该是一个道hard题目了。

除了这些难点，本题还有细节，例如：切割过的地方不能重复切割所以递归函数需要传入i + 1。

树形结构如下：

子集问题

子集问题（一）

在 78.子集 中讲解了子集问题，在树形结构中子集问题是要收集所有节点的结果，而组合问题是收集叶子节点的结果。

如图：

认清这个本质之后，今天的题目就是一道模板题了。

本题其实可以不需要加终止条件，因为startIndex >= nums.length，本层 for 循环本来也结束了，本来我们就要遍历整棵树。

有的同学可能担心不写终止条件会不会无限递归？

并不会，因为每次递归的下一层就是从i+1开始的。

如果要写终止条件，注意：result.add(path);要放在终止条件的上面，如下：

result.add(new LinkedList<>(path)); // 收集子集，要放在终止添加的上面，否则会漏掉结果
if (startIndex >= nums.length) { // 终止条件可以不加
    return;
}

子集问题（二）

在 90.子集Ⅱ 中，开始针对子集问题进行去重。

代码随想录算法day21 | 回溯算法part03 | 93.复原IP地址， 78.子集，90.子集II-优快云博客

本题就是 78.子集 的基础上加上了去重，去重我们在 40.组合总和Ⅱ 也讲过了，一样的套路。

树形结构如下：

递增子序列

在 491.递增子序列 中，处处都能看到子集的身影，但处处是陷阱，值得好好琢磨琢磨！

代码随想录算法day22 | 回溯算法part04 | 491.递增子序列，46.全排列，47.全排列 II-优快云博客

树形结构如下： 

很多同学都会把这道题目和 90. 子集Ⅱ 混在一起。

90. 子集Ⅱ 也可以使用 HashSet 针对同一父节点本层去重，但子集问题一定要排序，为什么呢？

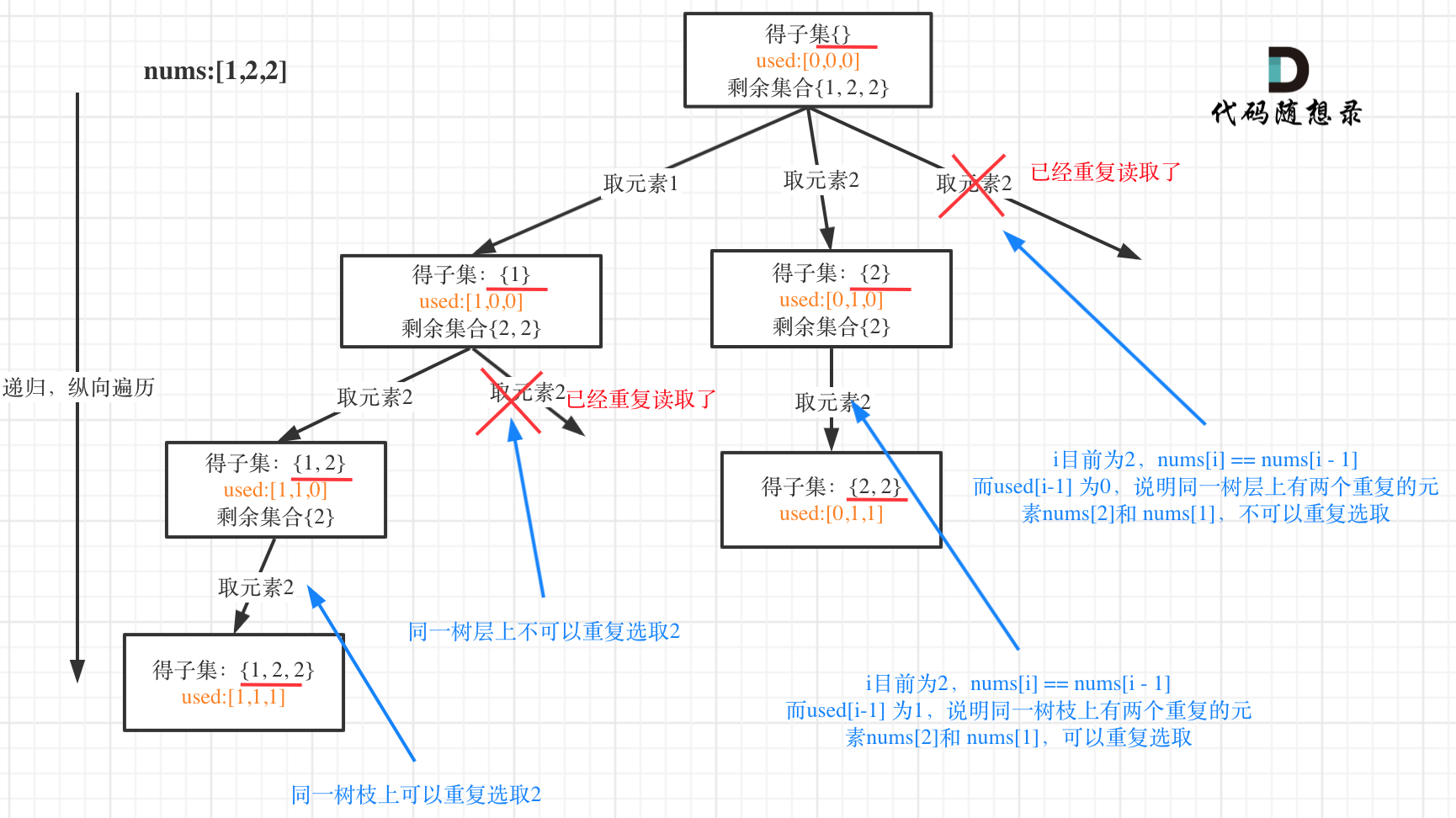
我用没有排序的集合{2,1,2,2}来举个例子画一个图，如下：

相信这个图胜过千言万语的解释了。

排列问题

排列问题（一）

46.全排列 又不一样了。

代码随想录算法day22 | 回溯算法part04 | 491.递增子序列，46.全排列，47.全排列 II-优快云博客

排列是有序的，也就是说 [1,2] 和 [2,1] 是两个集合，这和之前分析的子集以及组合所不同的地方。

可以看出元素1在[1,2]中已经使用过了，但是在[2,1]中还要在使用一次1，所以处理排列问题就不用使用startIndex了。

如图：

大家此时可以感受出排列问题的不同：

• 每层都是从 0 开始搜索而不是 startIndex
• 需要 used 数组记录 path 里都放了哪些元素了

排列问题（二）

排列问题也要去重了，在 47.全排列Ⅱ 中又一次强调了“树层去重”和“树枝去重”。

树形结构如下：

这道题目神奇的地方就是used[i - 1] == false也可以，used[i - 1] == true也可以！

我就用输入: [1,1,1] 来举一个例子。

树层上去重(used[i - 1] == false)，的树形结构如下：

树枝上去重（used[i - 1] == true）的树型结构如下：

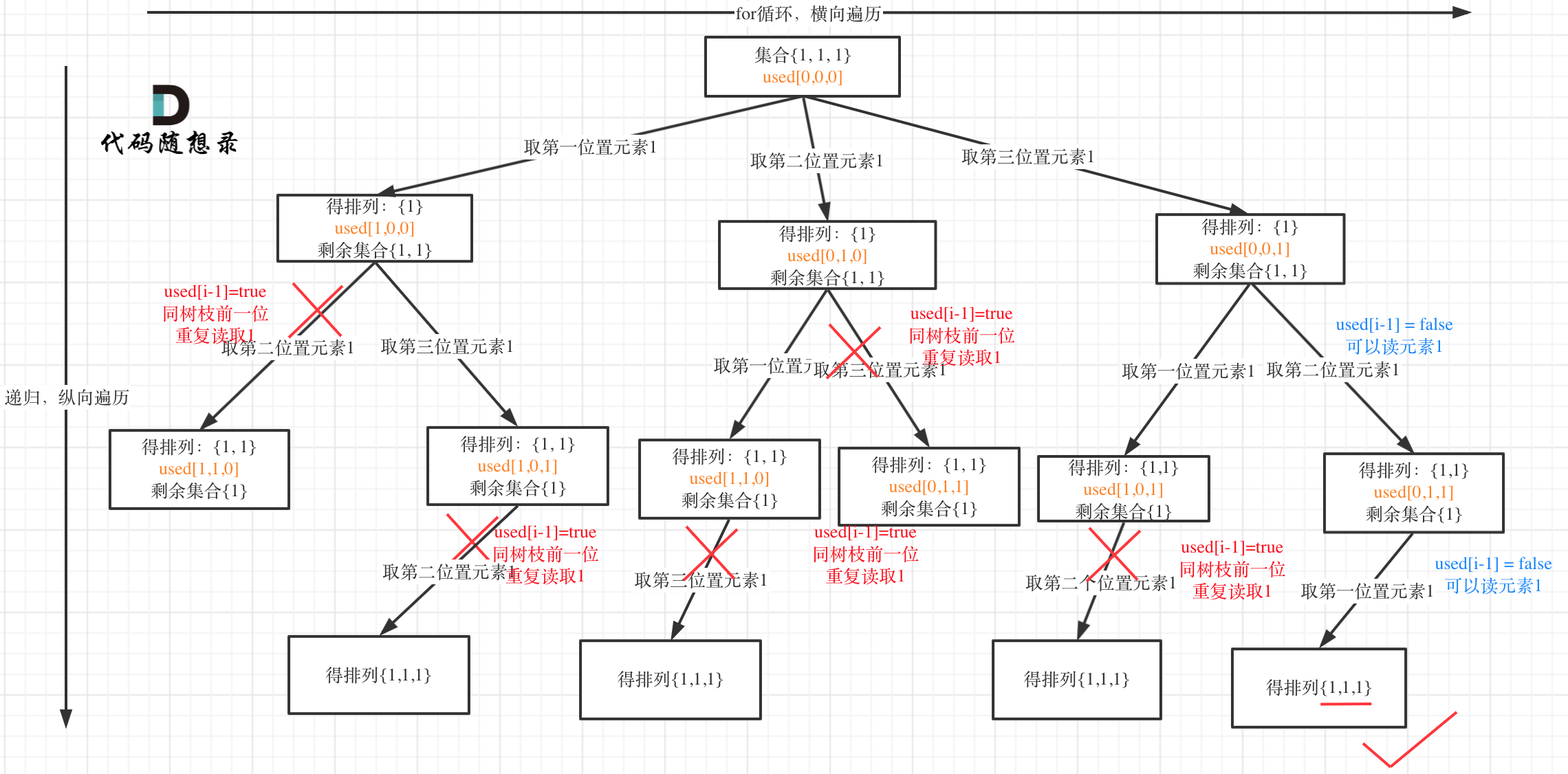
可以清晰的看到使用(used[i - 1] == false)，即树层去重，效率更高！

本题 used 数组即是记录 path 里都放了哪些元素，同时也用来去重，一举两得。​​​​​​​

性能分析

关于回溯算法的复杂度分析在网上的资料鱼龙混杂，一些所谓的经典面试书籍不讲回溯算法，算法书籍对这块也避而不谈，感觉就像是算法里模糊的边界。

所以这块就说一说我个人理解，对内容持开放态度，集思广益，欢迎大家来讨论！

以下在计算空间复杂度的时候我都把系统栈（不是数据结构里的栈）所占空间算进去。

子集问题分析：

• 时间复杂度：O(2^n)，因为每一个元素的状态无外乎取与不取，所以时间复杂度为O(2^n)
• 空间复杂度：O(n)，递归深度为n，所以系统栈所用空间为O(n)，每一层递归所用的空间都是常数级别，注意代码里的result和path都是全局变量，就算是放在参数里，传的也是引用，并不会新申请内存空间，最终空间复杂度为O(n)

排列问题分析：

• 时间复杂度：O(n!)，这个可以从排列的树形图中很明显发现，每一层节点为n，第二层每一个分支都延伸了n-1个分支，再往下又是n-2个分支，所以一直到叶子节点一共就是 n * n-1 * n-2 * ..... 1 = n!。
• 空间复杂度：O(n)，和子集问题同理。

组合问题分析：

• 时间复杂度：O(2^n)，组合问题其实就是一种子集的问题，所以组合问题最坏的情况，也不会超过子集问题的时间复杂度。
• 空间复杂度：O(n)，和子集问题同理。

一般说道回溯算法的复杂度，都说是指数级别的时间复杂度，这也算是一个概括吧！

总结

回溯专题汇聚为一张图：

这个图是 代码随想录知识星球 成员：莫非毛 (opens new window)，所画，总结的非常好，分享给大家。