笔者之前有一篇博客大致讲解了nginx源码中红黑树实现定时器的流程:Nginx事件模块学习之定时器_码农诗人的博客-优快云博客_nginx定时器;本章先不讨论红黑树算法的具体细节,借助nginx中的红黑树源码,将其抽离出来并实现一个简单的定时器的demo。
首先,将nginx源码中ngx_rbtree.h、ngx_rbtree.c两个文件拷贝出来,对其做一下简单修改,使其不再依赖nginx项目源码。
ngx_rbtree.h 具体代码如下:
/*
* Copyright (C) Igor Sysoev
* Copyright (C) Nginx, Inc.
*/
#ifndef _NGX_RBTREE_H_INCLUDED_
#define _NGX_RBTREE_H_INCLUDED_
#include <stdio.h>
typedef unsigned int ngx_rbtree_key_t;
typedef int ngx_rbtree_key_int_t;
typedef unsigned char u_char;
typedef struct ngx_rbtree_node_s ngx_rbtree_node_t;
struct ngx_rbtree_node_s {
ngx_rbtree_key_t key;
ngx_rbtree_node_t *left;
ngx_rbtree_node_t *right;
ngx_rbtree_node_t *parent;
u_char color;
u_char data;
};
typedef struct ngx_rbtree_s ngx_rbtree_t;
typedef void (*ngx_rbtree_insert_pt) (ngx_rbtree_node_t *root,
ngx_rbtree_node_t *node, ngx_rbtree_node_t *sentinel);
struct ngx_rbtree_s {
ngx_rbtree_node_t *root;
ngx_rbtree_node_t *sentinel;
ngx_rbtree_insert_pt insert;
};
#define ngx_rbtree_init(tree, s, i) \
ngx_rbtree_sentinel_init(s); \
(tree)->root = s; \
(tree)->sentinel = s; \
(tree)->insert = i
void ngx_rbtree_insert(ngx_rbtree_t *tree, ngx_rbtree_node_t *node);
void ngx_rbtree_delete(ngx_rbtree_t *tree, ngx_rbtree_node_t *node);
void ngx_rbtree_insert_value(ngx_rbtree_node_t *root, ngx_rbtree_node_t *node,
ngx_rbtree_node_t *sentinel);
void ngx_rbtree_insert_timer_value(ngx_rbtree_node_t *root,
ngx_rbtree_node_t *node, ngx_rbtree_node_t *sentinel);
ngx_rbtree_node_t *ngx_rbtree_next(ngx_rbtree_t *tree,
ngx_rbtree_node_t *node);
#define ngx_rbt_red(node) ((node)->color = 1)
#define ngx_rbt_black(node) ((node)->color = 0)
#define ngx_rbt_is_red(node) ((node)->color)
#define ngx_rbt_is_black(node) (!ngx_rbt_is_red(node))
#define ngx_rbt_copy_color(n1, n2) (n1->color = n2->color)
/* a sentinel must be black */
#define ngx_rbtree_sentinel_init(node) ngx_rbt_black(node)
static inline ngx_rbtree_node_t *
ngx_rbtree_min(ngx_rbtree_node_t *node, ngx_rbtree_node_t *sentinel)
{
while (node->left != sentinel) {
node = node->left;
}
return node;
}
#endif /* _NGX_RBTREE_H_INCLUDED_ */
ngx_rbtree.c 具体代码如下:
/*
* Copyright (C) Igor Sysoev
* Copyright (C) Nginx, Inc.
*/
#include "ngx_rbtree.h"
/*
* The red-black tree code is based on the algorithm described in
* the "Introduction to Algorithms" by Cormen, Leiserson and Rivest.
*/
static inline void ngx_rbtree_left_rotate(ngx_rbtree_node_t **root,
ngx_rbtree_node_t *sentinel, ngx_rbtree_node_t *node);
static inline void ngx_rbtree_right_rotate(ngx_rbtree_node_t **root,
ngx_rbtree_node_t *sentinel, ngx_rbtree_node_t *node);
void
ngx_rbtree_insert(ngx_rbtree_t *tree, ngx_rbtree_node_t *node)
{
ngx_rbtree_node_t **root, *temp, *sentinel;
/* a binary tree insert */
root = &tree->root;
sentinel = tree->sentinel;
if (*root == sentinel) {
node->parent = NULL;
node->left = sentinel;
node->right = sentinel;
ngx_rbt_black(node);
*root = node;
return;
}
tree->insert(*root, node, sentinel);
/* re-balance tree */
while (node != *root && ngx_rbt_is_red(node->parent)) {
if (node->parent == node->parent->parent->left) {
temp = node->parent->parent->right;
if (ngx_rbt_is_red(temp)) {
ngx_rbt_black(node->parent);
ngx_rbt_black(temp);
ngx_rbt_red(node->parent->parent);
node = node->parent->parent;
} else {
if (node == node->parent->right) {
node = node->parent;
ngx_rbtree_left_rotate(root, sentinel, node);
}
ngx_rbt_black(node->parent);
ngx_rbt_red(node->parent->parent);
ngx_rbtree_right_rotate(root, sentinel, node->parent->parent);
}
} else {
temp = node->parent->parent->left;
if (ngx_rbt_is_red(temp)) {
ngx_rbt_black(node->parent);
ngx_rbt_black(temp);
ngx_rbt_red(node->parent->parent);
node = node->parent->parent;
} else {
if (node == node->parent->left) {
node = node->parent;
ngx_rbtree_right_rotate(root, sentinel, node);
}
ngx_rbt_black(node->parent);
ngx_rbt_red(node->parent->parent);
ngx_rbtree_left_rotate(root, sentinel, node->parent->parent);
}
}
}
ngx_rbt_black(*root);
}
void
ngx_rbtree_insert_value(ngx_rbtree_node_t *temp, ngx_rbtree_node_t *node,
ngx_rbtree_node_t *sentinel)
{
ngx_rbtree_node_t **p;
for ( ;; ) {
p = (node->key < temp->key) ? &temp->left : &temp->right;
if (*p == sentinel) {
break;
}
temp = *p;
}
*p = node;
node->parent = temp;
node->left = sentinel;
node->right = sentinel;
ngx_rbt_red(node);
}
void
ngx_rbtree_insert_timer_value(ngx_rbtree_node_t *temp, ngx_rbtree_node_t *node,
ngx_rbtree_node_t *sentinel)
{
ngx_rbtree_node_t **p;
for ( ;; ) {
/*
* Timer values
* 1) are spread in small range, usually several minutes,
* 2) and overflow each 49 days, if milliseconds are stored in 32 bits.
* The comparison takes into account that overflow.
*/
/*
// map 实现 key相同覆盖
if(node->key == temp->key){
temp->data = node->data;
break;
}
*/
/* node->key < temp->key */
p = ((ngx_rbtree_key_int_t) (node->key - temp->key) < 0)
? &temp->left : &temp->right;
if (*p == sentinel) {
break;
}
temp = *p;
}
*p = node;
node->parent = temp;
node->left = sentinel;
node->right = sentinel;
ngx_rbt_red(node);
}
void
ngx_rbtree_delete(ngx_rbtree_t *tree, ngx_rbtree_node_t *node)
{
unsigned int red;
ngx_rbtree_node_t **root, *sentinel, *subst, *temp, *w;
/* a binary tree delete */
root = &tree->root;
sentinel = tree->sentinel;
if (node->left == sentinel) {
temp = node->right;
subst = node;
} else if (node->right == sentinel) {
temp = node->left;
subst = node;
} else {
subst = ngx_rbtree_min(node->right, sentinel);
if (subst->left != sentinel) {
temp = subst->left;
} else {
temp = subst->right;
}
}
if (subst == *root) {
*root = temp;
ngx_rbt_black(temp);
/* DEBUG stuff */
node->left = NULL;
node->right = NULL;
node->parent = NULL;
node->key = 0;
return;
}
red = ngx_rbt_is_red(subst);
if (subst == subst->parent->left) {
subst->parent->left = temp;
} else {
subst->parent->right = temp;
}
if (subst == node) {
temp->parent = subst->parent;
} else {
if (subst->parent == node) {
temp->parent = subst;
} else {
temp->parent = subst->parent;
}
subst->left = node->left;
subst->right = node->right;
subst->parent = node->parent;
ngx_rbt_copy_color(subst, node);
if (node == *root) {
*root = subst;
} else {
if (node == node->parent->left) {
node->parent->left = subst;
} else {
node->parent->right = subst;
}
}
if (subst->left != sentinel) {
subst->left->parent = subst;
}
if (subst->right != sentinel) {
subst->right->parent = subst;
}
}
/* DEBUG stuff */
node->left = NULL;
node->right = NULL;
node->parent = NULL;
node->key = 0;
if (red) {
return;
}
/* a delete fixup */
while (temp != *root && ngx_rbt_is_black(temp)) {
if (temp == temp->parent->left) {
w = temp->parent->right;
if (ngx_rbt_is_red(w)) {
ngx_rbt_black(w);
ngx_rbt_red(temp->parent);
ngx_rbtree_left_rotate(root, sentinel, temp->parent);
w = temp->parent->right;
}
if (ngx_rbt_is_black(w->left) && ngx_rbt_is_black(w->right)) {
ngx_rbt_red(w);
temp = temp->parent;
} else {
if (ngx_rbt_is_black(w->right)) {
ngx_rbt_black(w->left);
ngx_rbt_red(w);
ngx_rbtree_right_rotate(root, sentinel, w);
w = temp->parent->right;
}
ngx_rbt_copy_color(w, temp->parent);
ngx_rbt_black(temp->parent);
ngx_rbt_black(w->right);
ngx_rbtree_left_rotate(root, sentinel, temp->parent);
temp = *root;
}
} else {
w = temp->parent->left;
if (ngx_rbt_is_red(w)) {
ngx_rbt_black(w);
ngx_rbt_red(temp->parent);
ngx_rbtree_right_rotate(root, sentinel, temp->parent);
w = temp->parent->left;
}
if (ngx_rbt_is_black(w->left) && ngx_rbt_is_black(w->right)) {
ngx_rbt_red(w);
temp = temp->parent;
} else {
if (ngx_rbt_is_black(w->left)) {
ngx_rbt_black(w->right);
ngx_rbt_red(w);
ngx_rbtree_left_rotate(root, sentinel, w);
w = temp->parent->left;
}
ngx_rbt_copy_color(w, temp->parent);
ngx_rbt_black(temp->parent);
ngx_rbt_black(w->left);
ngx_rbtree_right_rotate(root, sentinel, temp->parent);
temp = *root;
}
}
}
ngx_rbt_black(temp);
}
static inline void
ngx_rbtree_left_rotate(ngx_rbtree_node_t **root, ngx_rbtree_node_t *sentinel,
ngx_rbtree_node_t *node)
{
ngx_rbtree_node_t *temp;
temp = node->right;
node->right = temp->left;
if (temp->left != sentinel) {
temp->left->parent = node;
}
temp->parent = node->parent;
if (node == *root) {
*root = temp;
} else if (node == node->parent->left) {
node->parent->left = temp;
} else {
node->parent->right = temp;
}
temp->left = node;
node->parent = temp;
}
static inline void
ngx_rbtree_right_rotate(ngx_rbtree_node_t **root, ngx_rbtree_node_t *sentinel,
ngx_rbtree_node_t *node)
{
ngx_rbtree_node_t *temp;
temp = node->left;
node->left = temp->right;
if (temp->right != sentinel) {
temp->right->parent = node;
}
temp->parent = node->parent;
if (node == *root) {
*root = temp;
} else if (node == node->parent->right) {
node->parent->right = temp;
} else {
node->parent->left = temp;
}
temp->right = node;
node->parent = temp;
}
ngx_rbtree_node_t *
ngx_rbtree_next(ngx_rbtree_t *tree, ngx_rbtree_node_t *node)
{
ngx_rbtree_node_t *root, *sentinel, *parent;
sentinel = tree->sentinel;
if (node->right != sentinel) {
return ngx_rbtree_min(node->right, sentinel);
}
root = tree->root;
for ( ;; ) {
parent = node->parent;
if (node == root) {
return NULL;
}
if (node == parent->left) {
return parent;
}
node = parent;
}
}
下来构建一下自己定时器头文件my_timer.h,具体代码如下:
/***********************************************
* Author : lijd
* Date : 2022-11-15
* Func : 借助nginx红黑树源码实现简单定时器
***********************************************/
#ifndef _LIJD_MY_TIMER_
#define _LIJD_MY_TIMER_
#include <stdlib.h>
#include <string.h>
#include <stddef.h>
#include <time.h>
#include <stdio.h>
#include <pthread.h>
#include "ngx_rbtree.h"
// 定时器树结构定义
ngx_rbtree_t my_timer;
// 定时器哨兵节点定义,用作初始化
ngx_rbtree_node_t my_sentinel;
typedef unsigned int uint_32;
typedef struct my_timer_entry_s my_timer_entry_t;
typedef void (*my_timer_callback_pt) (my_timer_entry_t *mte);
// 定时器结构定义
struct my_timer_entry_s {
ngx_rbtree_node_t rbnode; // 红黑树节点,用作生成红黑树
my_timer_callback_pt cb; // 到期执行的回调函数
void *data; // 回调函数的传入参数
};
// 获取当前时间的毫秒值(CLOCK_MONOTONIC:系统启动相对时间)
uint_32 my_currtime() {
struct timespec tv = {0};
clock_gettime(CLOCK_MONOTONIC, &tv);
uint_32 t = tv.tv_sec * 1000;
t += tv.tv_nsec / 1000000;
return t;
}
// 初始化定时器树结构
void my_init_timer() {
ngx_rbtree_init(&my_timer, &my_sentinel, ngx_rbtree_insert_timer_value);
}
// 定时器结构添加节点
my_timer_entry_t * my_add_timer(uint_32 key, my_timer_callback_pt cb, void *data) {
my_timer_entry_t *mte = (my_timer_entry_t *)malloc(sizeof(my_timer_entry_t));
if(mte != NULL){
memset(mte, 0, sizeof(my_timer_entry_t));
mte->rbnode.key = my_currtime() + key;
mte->cb = cb;
mte->data = data;
printf("pthread id: %x, add timer key : %u\n", pthread_self(), mte->rbnode.key);
ngx_rbtree_insert(&my_timer, &mte->rbnode);
}
return mte;
}
// 定时器结构删除节点
void my_del_timer(my_timer_entry_t *mte) {
if(mte != NULL) {
ngx_rbtree_delete(&my_timer, &mte->rbnode);
free(mte);
}
}
// 处理定时任务
void my_handle_timer() {
my_timer_entry_t *mte;
ngx_rbtree_node_t *root, *node;
for(;;) {
root = my_timer.root;
// 空树
if(root == my_timer.sentinel) break;
node = ngx_rbtree_min(root, my_timer.sentinel);
// 最近的事件还没到达触发时间
if(node->key > my_currtime()) break;
// 存在事件需触发,将node转换为自定义结构
mte = (my_timer_entry_t *)((char *)node - offsetof(my_timer_entry_t, rbnode));
// 回调函数调用
mte->cb(mte);
// 定时器树上删除已执行节点
my_del_timer(mte);
}
}
// 查找时间的最小触发时间
int my_find_nearest_timer() {
if(my_timer.root == my_timer.sentinel) return -1;
ngx_rbtree_node_t *node = ngx_rbtree_min(my_timer.root, my_timer.sentinel);
if(node->key <= my_currtime()) return -1;
return (int)(node->key - my_currtime());
}
#endif /* _LIJD_MY_TIMER_ */
由于nginx中的网络事件用epoll处理的,我们的测试用例尽量接近nginx环境。测试用例中:主要创建一个线程去随机生产定时任务,主线程去处理epoll事件和定时任务事件)。具体代码如下:
/***********************************************
* Author : lijd
* Date : 2022-11-15
* Func : 测试定时器功能主函数
***********************************************/
#include <stdio.h>
#include <sys/epoll.h>
#include <pthread.h>
#include <unistd.h>
#include "ngx_rbtree.h"
#include "my_timer.h"
// 定时器回调函数
void test(my_timer_entry_t *mte) {
printf("pthread id : %x, test time callback : %u \n", pthread_self(), mte->rbnode.key);
}
// 随机生成定时器事件
void* handler_thread(void *arg) {
my_init_timer();
for(;;) {
srand((unsigned int)time(NULL));
int ret=rand() % 10;
my_add_timer(ret * 1000, test, NULL);
sleep(5);
}
pthread_exit(NULL);
}
int main()
{
pthread_t pid;
int i;
// 创建生成定时器事件线程
pthread_create(&pid, NULL, handler_thread, NULL);
int epfd = epoll_create(1);
struct epoll_event events[512];
// 定时器中的事件:网络事件 + 其它定时事件
// 如果其它定时事件的最小key(执行时间) > nowtime(当前时间) : 说明有事件需要触发,需立即执行
// 否则,网络事件的阻塞时间(timeout) = 其它最近触发的定时事件 - nowtime
// 这样既兼顾了其它事件 也 兼顾了网络事件
for(;;) {
// epoll_wait 为阻塞的系统调用
// timeout 为阻塞时间(-1:一直阻塞,直到事件发生,>=0 表示阻塞最多时间返回)
int timeout = (my_find_nearest_timer() >= 0 ? my_find_nearest_timer() : 10*1000);
printf("now time : %u, timeout : %d\n",my_currtime(), timeout);
int n = epoll_wait(epfd, events, 512, timeout);
for(i = 0; i < n; i++) {
// 处理网络事件
}
// 处理定时任务
my_handle_timer();
printf("-----------------------------------------------------\n\n");
}
pthread_join(pid, NULL);
return 0;
}执行结果如下图:
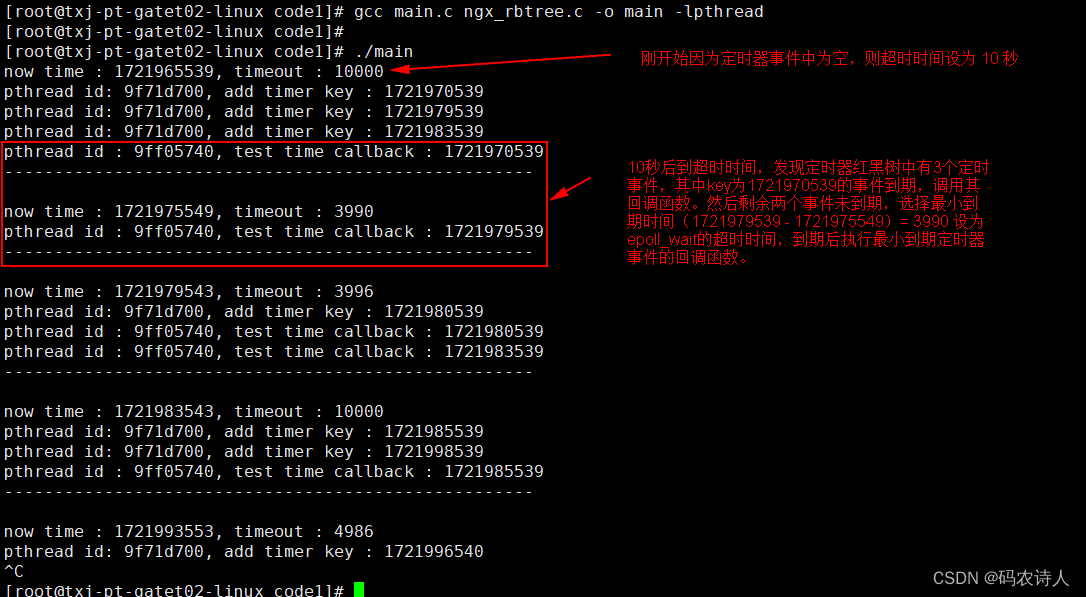





 本文介绍了如何从nginx源码中提取红黑树实现,并构建了一个简单的定时器。作者首先展示了修改后的ngx_rbtree.h和ngx_rbtree.c文件,使其独立于nginx项目。然后,创建了一个名为my_timer.h的头文件,定义了定时器结构和相关操作,如添加、删除和处理定时任务。最后,给出了一个测试用例,模拟了生成和处理定时任务的线程。测试用例中,一个线程随机添加定时任务,主线程处理这些任务。
本文介绍了如何从nginx源码中提取红黑树实现,并构建了一个简单的定时器。作者首先展示了修改后的ngx_rbtree.h和ngx_rbtree.c文件,使其独立于nginx项目。然后,创建了一个名为my_timer.h的头文件,定义了定时器结构和相关操作,如添加、删除和处理定时任务。最后,给出了一个测试用例,模拟了生成和处理定时任务的线程。测试用例中,一个线程随机添加定时任务,主线程处理这些任务。

















 1056
1056

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








