现代藏宝图分割法则 — 纠删码

引言    

很久很久以前，有五位大侠找到了一张巨大无比的藏宝图，于是商榷过后打算一分为五，十年后相约开启，结果其中一位发生意外陨落了，所持有的那一片藏宝图也随之销毁，宝物无人能得，大侠们抱憾终生，约定来生再战。

重生之五位大侠，回到了故事开头

很久很久以前，有五位大侠找到了一张巨大无比的藏宝图，有了前车之鉴，打算一人复制一份，十年后相约开启，结果因太大不便于携带，其中一份意外泄露，结果十年后，藏宝洞口人山人海，一场混战，五位大侠在混乱中战死了。

提问：五位大侠应该怎么分最合理？

一份藏宝图一分为三，对三份藏宝图碎片进行编码，然后得到两份校验码，这样的话编码+校验码一共就有五份，由五人分别持有，即使泄露两份，也不会暴露藏宝图完整信息，即使销毁两份，剩下的仍可以解码出完整藏宝图。

而这就是纠删码的基本原理，纠删码获取原始数据并以这样一种方式对其进行编码，当需要数据时，它需要片段的子集来重新创建原始信息。

总数据块=原始数据块+校验块，即 t=k+n，纠删码技术允许在数据存储中任意n个块损坏的场景中恢复出数据。

     一、概念     

纠删码（Erasure Code，也叫擦除码）是一种编码容错技术。最早用于通信行业，数据传输中的数据恢复。它通过对数据进行分块，然后计算出校验数据，使得各个部分的数据产生关联性。当一部分数据块丢失时，可以通过剩余的数据块和校验块计算出丢失的数据块。纠删码只能容忍数据丢失，无法容忍数据篡改，纠删码正是因此得名。

目前，纠删码技术中最广泛使用的是 Reed–Solomon 码，由麻省理工学院林肯实验室的 Irving S. Reed 和 Gustave Solomon 于1960年在 Polynomial Codes over Certain Finite Fields 中提及。

Reed-Solomon 码广泛应用于多个领域：

• 用于存储设备，如 CD、DVD 等。

• 用于无线或移动通信中进行数据传输。

• 用于卫星通信。

• 用于数字电视。

• 用于高速调制解调器。

• 用于条码、二维码。

• 用于企业存储环境。

     二、原理     

以存储为例，让我们看看 RS 码是怎么实现容错的。

举个简单的栗子：

藏宝洞开启的咒语为123，五位大侠将咒语划分为三份，通过预设的编码矩阵，可得：

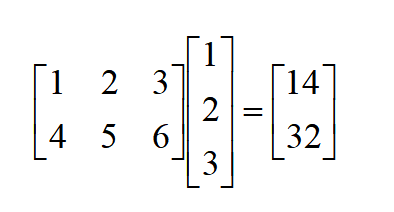
则此时数据块D1=1，D2=2，D3=3，校验块P1=14，P2=32，五位大侠分别保存，若丢失D1和D2，那么分别设丢失数据为 x，y，则：

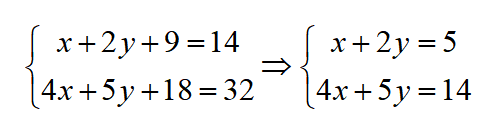
易解得D1和D2的原始值，因此，可以从五个块之中的任意两个获得原始信息。换言之，两点可以确定一条直线。

同样的事情也适用于n次多项式，可以将一条线称为 1 次多项式，2 次多项式更常见地称为二次方程或抛物线，3次多项式通常称为三次方程。

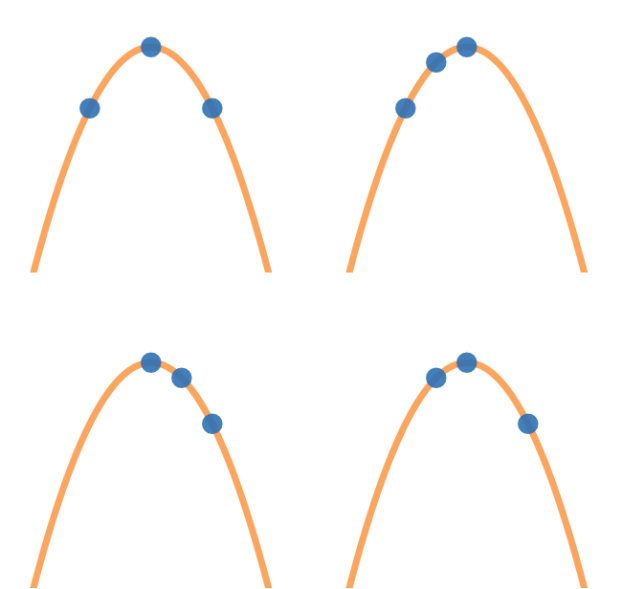
任意 3 个点唯一确定一个 2 次多项式，任意 4 个点唯一确定一个 3 次多项式。通常，任何n+1个点唯一确定一个n次多项式。

把数据分片形成多个点，校验码也是多项式上的点，则当我们像例子中有5个点时，只需要3个点就能唯一确定一个多项式。

当然，现实情况往往没有这么简单。

现如今，编码矩阵的构造方式越来越多样化，编码矩阵的选择以保证可逆性条件的满足为主，这里以原始的 Vandermonde 矩阵为例：

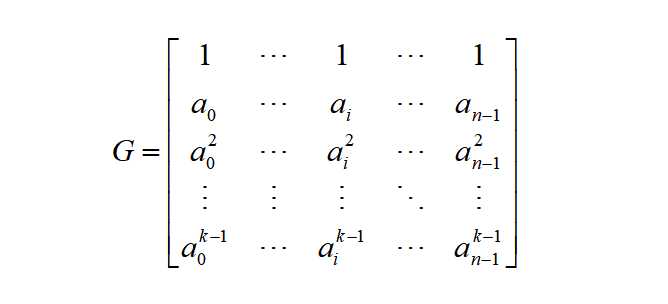
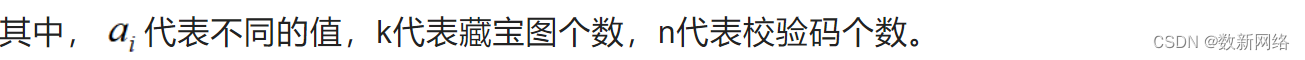
通过单位矩阵和 Vandermonde 矩阵的组合构建编码矩阵。输入数据D和编码矩阵的乘积就是编码后的数据，得到校验块P。 

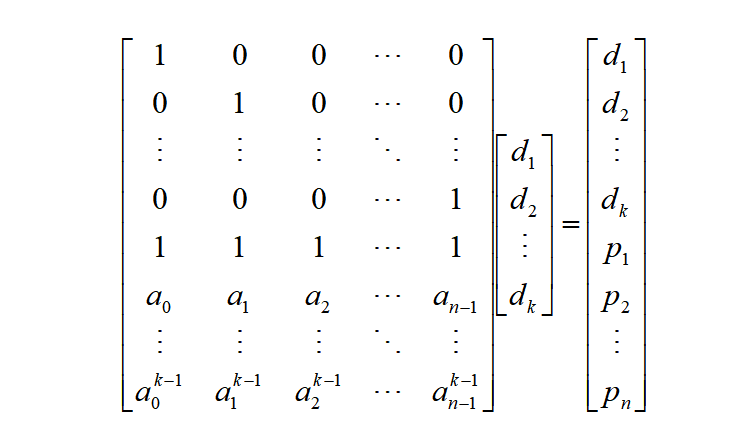
而从某种角度来讲，矩阵的运算其实就是多项式的运算。

     三、应用     

纠删码以更低的存储成本备受青睐，目前 Microsoft、Google、Facebook、Amazon、淘宝（TFS）都已经在自己的产品中采用了 Erasure Code。应用范围包括：

• 磁盘阵列系统

• 数据网格

• 分布式存储应用

• 对象存储

• 档案存储

当前一种常见的纠删码用例是基于对象的云存储。由于纠删码需要较高的 CPU 利用率并会产生延迟，因此它适用于归档应用程序。

而以分布式存储为例，通常采用冗余副本的方式，即对存储的数据进行副本备份，当数据出现丢失，损坏，即可使用备份内容进行恢复，而副本备份的多少，决定了数据可靠性的高低。从大侠们的故事很容易看出，这种方式安全性比较低，占用空间大，成本高，冗余率高，由于每个副本都是完整副本，因此很容易受到非法访问，而加密带来的密钥管理复杂性也是一个问题。当前已有很多分布式系统是采用此种方式实现，如 Hadoop 的文件系统（3个副本），Redis 的集群，MySQL 的主备模式等。而如 MinIO 和 Hadoop3.0 等则使用了纠删码进行容灾恢复，低冗余且磁盘损坏高容忍，高磁盘利用率。

四、特性     

综上所述，纠删码的优点有很多：

• 存储空间利用率： 纠删码通过减少占用的空间并提供相同级别的冗余（3 个副本）来提供更好的存储利用率，使用纠删码可节省多达 50% 的空间。

• 更高的可靠性： 数据片段被分割成独立的块，确保故障没有关联性。

• 适用性：纠删码可用于任何文件大小。从 KiloBytes 的小块大小到 PetaBytes 的大块大小。

• 仅子集：只需要数据子集即可恢复数据，不需要原始数据。

• 灵活性：可以在方便时更换故障组件，而无需使系统脱机。如果在读的过程中发现数据丢失，能够立即解码出丢失的数据从而不影响读操作。

• 安全性：不可能从单个分片中获取全部源数据。

相反，纠删码也有一些缺点：

• 数据恢复代价高。丢失数据块或者编码块时， RS需要读取n个数据块和校验块才能恢复数据，数据恢复效率也在一定程度上制约了RS的可靠性。

• 数据更新代价高。数据更新相当于重新编码， 代价很高， 因此常常针对只读数据，或者冷数据。

纠删码所带来的额外负担主要是计算量和数倍的网络负载，一般对于热数据还是会使用多副本策略来冗余，冷数据使用纠删码。

而现实应用中，会根据其特性做一些优化。

首先是 LRC（Locally Repairable Code），原理如下图所示：

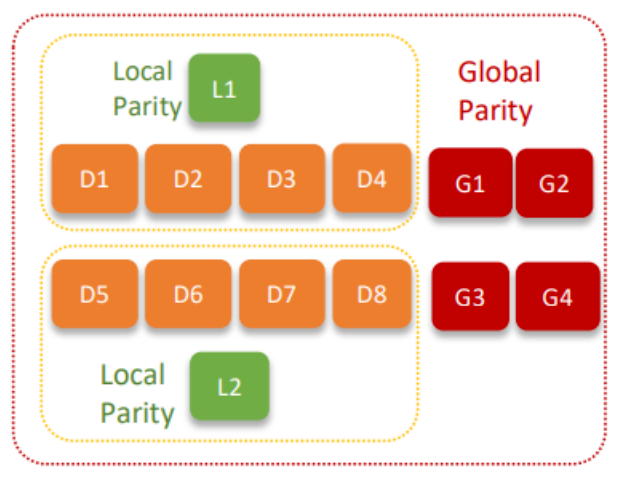
而其对策就是分组，在 RS 的基础上把单个磁盘故障影响范围缩小到各个组内部，出坏盘故障时，该组内部解决，在恢复过程中读组内更少的盘，跑更少的网络流量，从而减小对全局的影响。

同时也衍生出了 SEC（Sparse Erasure Code），增加了对全局校验块的校验块生成，减少了恢复数据时的网络和CPU开销。

✎ 写在最后 

随着海量存储系统的发展和在复杂环境中的应用，存储系统的可靠性受到了严重的挑战.纠删码在存储系统容错方向的使用越来越受到重视。目前不同纠删码在容错能力、计算效率、存储利用率等方面都存在不同程度的缺陷，如何平衡这些影响纠删码性能的因素，设计出更高容错能力、更高计算效率及更高存储利用率的纠删码，仍是未来很长一段时间内值得不断深入研究的问题。

本期内容就到这里了，如果喜欢就点个关注吧，微信公众号搜索“数 新 网 络 科 技 号”可查看更多精彩内容~