何为RMQ
在文章《Tarjan’s off-line lowest common ancestors algorithm》我们用图形化的方式展示了Tarjan’s off-line LCA的求解过程,但是该文章有很多遗漏,例如下面的这些问题。在本篇文章中,我会介绍另外一种求解LCA的方法,然后尝试顺带回答列出的这些问题。
- 既然有了Leetcode 236中标准解法,为什么还需要Tarjan这种比较重的方法?
- 在那篇文章中,提到Tarjan方法的本质是并查集,但是那种说法并不严谨,并查集只是Tarjan实现途径
现阶段比较好的求解LCA的方式是基于RMQ的求解方法,本文章会着重介绍什么是RMQ以及常见的几种求解RMQ的方法,
注:本篇文章完全按照TopCoder中的此篇文章展开的,所以如果看过那篇文章就不用浪费时间本篇文章了
RMQ,全称Range minimum query,用于查询一个数组中子数组的最值,这样一个看似简单的问题,却有很多值得玩味的地方。
In computer science, a range minimum query (RMQ) solves the problem of finding the minimal value in a sub-array of an array of comparable objects. 《Range minimum query》
朴素解法
例如,给定包含
N
N
N个数的数组
A
[
N
]
A[N]
A[N]和
Q
Q
Q个查询。每个查询的输入
(
a
,
b
)
(a, b)
(a,b)都是一对整数,要求打印出
A
[
a
]
A[a]
A[a]到
A
[
b
]
A[b]
A[b]之间的最大值和最小值之差。例如,
N
=
6
N = 6
N=6,
Q
=
3
Q = 3
Q=3,一个输入样例是
注:此问题来源于《数据结构:线段树》
A
:
1
7
3
4
2
5
6
9
A\ :\ 1\ 7\ 3\ 4\ 2\ 5\ 6\ 9
A : 1 7 3 4 2 5 6 9
q
u
e
r
y
:
0
4
query: 0\ 4
query:0 4
3
5
\qquad \quad \ \ 3\ 5
3 5
1
1
\qquad \quad \ \ 1\ 1
1 1
比较直观的方法是先得到Max和Min,然后求差值,在数组没有发生变化的情况下,这种方法有很多资源的浪费,存在很多重复计算。例如我们在查询( 1 1 1, 5 5 5)之间Max和Min,可以顺手将子区间的最大值和最小值记录下来,使用一种Record Table来存储计算后的结果。
Record Table
显而易见将所有可能的查询下标对( a a a, b b b)记录下来,需要 O ( N 2 ) O(N^2) O(N2)的空间复杂度。求子数组最小值的记录表格如下所示:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 7 | 3 | 3 | 2 | 2 | 2 | 2 | |
| 2 | 3 | 3 | 2 | 2 | 2 | 2 | ||
| 3 | 4 | 2 | 2 | 2 | 2 | |||
| 4 | 2 | 2 | 2 | 2 | ||||
| 5 | 5 | 5 | 5 | |||||
| 6 | 6 | 6 | ||||||
| 7 | 9 |
该方法的复杂度如下所示:
- 前期准备工作,亦即计算该表格的时间复杂度为 O ( N 2 ) O(N^2) O(N2)
- 查询复杂度为 O ( 1 ) O(1) O(1)
- 空间复杂度为 O ( N 2 ) O(N^2) O(N2),
该方法的查询复杂度虽然很低,但是空间复杂度却比较高,那么是否可以对存储的表格进行精简?
可以使用动态规划来求解该表格,注意对Table[i][i]的赋值移动到双层loop中,但是那种做法没有下面这种形式高效,经过我在quick-bench上的测试,下面的这种形式比另外一种形式快1.6倍,测试结果见http://quick-bench.com/oTprU_S6yaNvqI2xpjtBemq9O4w。下面这种方式比较快的原因可能是C++中的not pay for what you don’t use,类似于copy-and-swap idiom相较于传统方式的优势。
#include <iostream>
#include <vector>
using TableType = std::vector<std::vector<int>>;
void solution(std::vector<int> &Array, TableType &Table) {
size_t size = Array.size();
for (int i = 0; i < size; ++i)
Table[i][i] = Array[i];
for (size_t i = 0; i < size; ++i) {
for (size_t j = i; j < size; ++j) {
if (Table[i][j-1] < Array[j])
Table[i][j] = Table[i][j-1];
else
Table[i][j] = Array[j];
}
}
}
int main() {
std::vector<int> Vec{1, 7, 3, 4, 2, 5, 6, 9};
TableType Table{Vec.size(), std::vector<int>(Vec.size(), 0)};
solution(Vec, Table);
return 0;
}
block-based Table
Sqrt-based Table
我们可以牺牲查询操作的效率,来得到更小的表格需要的存储空间。我们可以将 A [ N ] A[N] A[N]分成几个chunks,存储各chunk的最小值,然后将某次查询经由这些chunk的最小值组合而成,由于我们至多可以将 A A A分割成 N N N个chunk,所以存储空间至多为 O ( N ) O(N) O(N)。TopCoder直接将 A [ N ] A[N] A[N]分割成了 s q r t ( N ) sqrt(N) sqrt(N)个chunk,并没有解释缘由,GeekforGeeks中有一篇很好关于为什么常常将 A r r a y Array Array分割成 s q r t ( N ) sqrt(N) sqrt(N)的讲解,见Sqrt (or Square Root) Decomposition Technique | Set 1 (Introduction)。
The key concept of this technique is to decompose given array into small chunks specifically of size sqrt(n).
我们以开头数组为例,选择将
A
r
r
a
y
Array
Array分割成不同的chrunk,如下图所示:
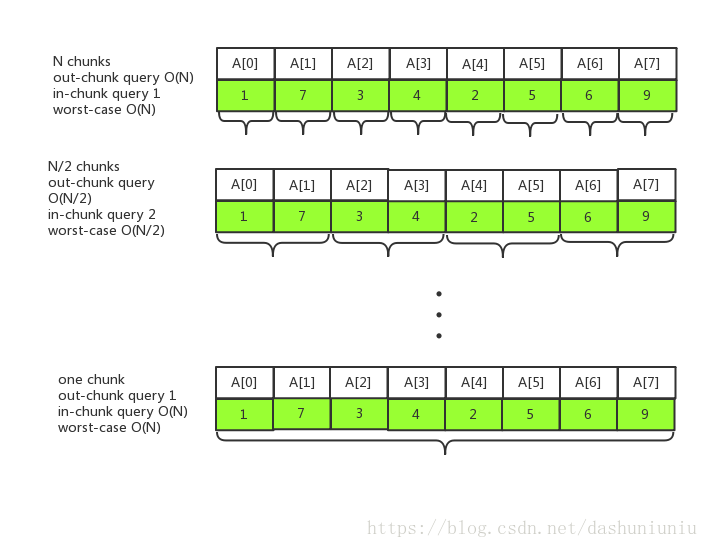
所以每次查询都可分为下面两种情况,查询的复杂度就可以通过下面两种情况中较大的复杂度决定。
- 查询跨越多个chunk
- 查询只局限在一个chunk中
那么分成几个chunk,才能使查询的最坏复杂度最小呢?答案是将长度为 N N N的 A r r a y Array Array分为 s q r t ( N ) sqrt(N) sqrt(N)个chunk时,worst case complexity最小。
Why sqrt is perfect?
假如我们将 W C ( N , x ) WC(N, x) WC(N,x)定义为将长度为 N N N的数组分割为 x x x个chunk的复杂度,那么该函数如下所示:
W
C
(
N
,
x
)
=
{
N
/
x
,
i
f
N
/
x
>
x
x
,
o
t
h
e
r
w
i
s
e
WC(N, x) = \begin{cases} N/x, \qquad {\rm if\ } N/x > x \\ x, \qquad \quad \ \ {\rm otherwise} \end{cases}
WC(N,x)={N/x,if N/x>xx, otherwise
当
x
x
x取
s
q
r
t
(
N
)
sqrt(N)
sqrt(N)时,
W
C
(
N
,
x
)
WC(N, x)
WC(N,x)达到最小值,如下图所示,也就是
8
/
x
8/x
8/x与
x
x
x交点的位置。
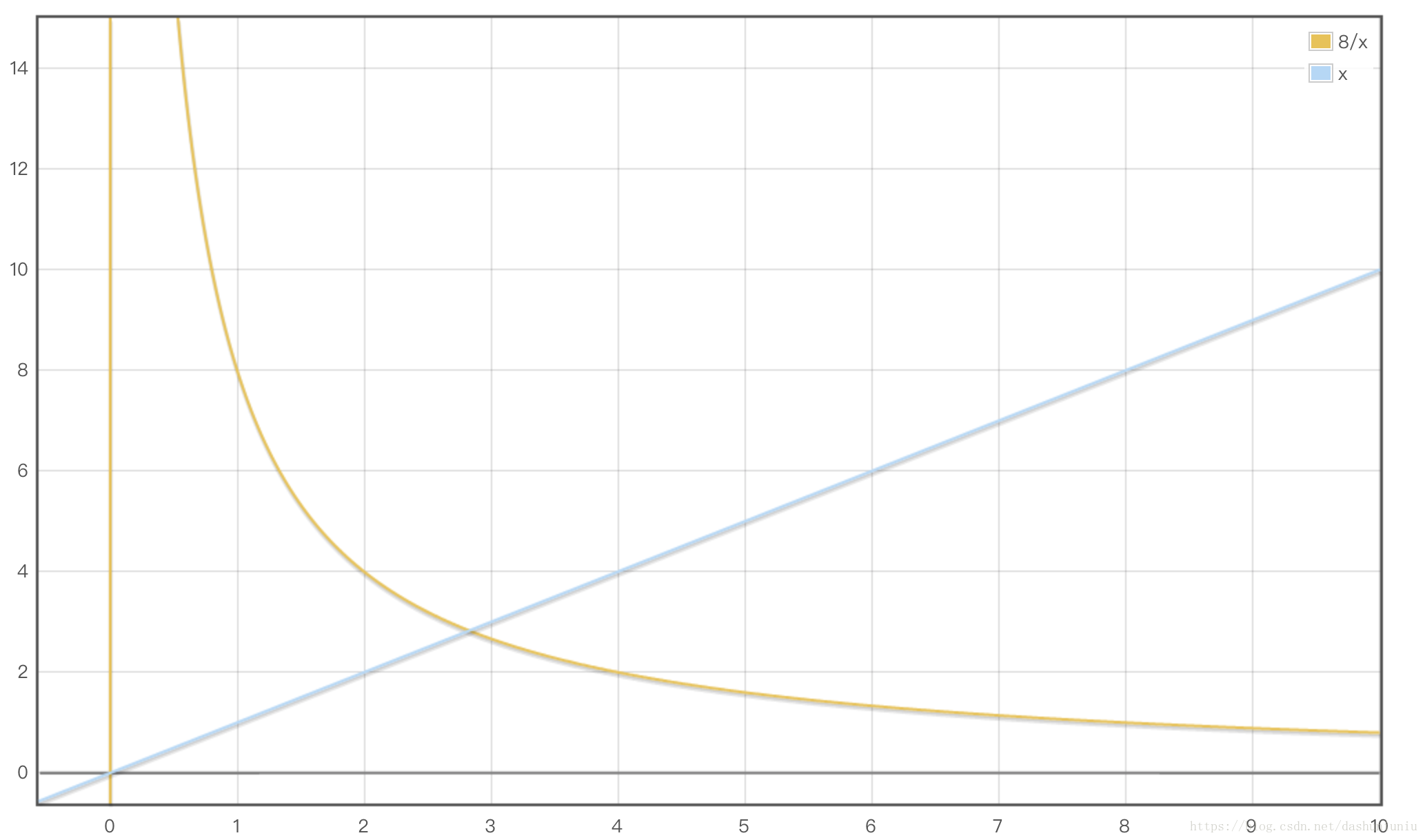
此时空间复杂度为 O ( s q r t ( N ) ) O(sqrt(N)) O(sqrt(N)),查询复杂度为 O ( s q r t ( N ) ) O(sqrt(N)) O(sqrt(N)),构建Table的复杂度是 O ( N ) O(N) O(N)。
泛华形式
Sparse Table
注:该小节的标题其实不是很合适,sparse table是一个很宽泛的概念,上一小节中的block-based table其实也可以算作这一小节中
现如今针对RMQ中的sparse table就特指文章《The LCA Problem Revisited》中提出的sparse table的方法(注:也是该篇文章首次将LCA问题转换成RMQ问题求解的)。该方法首先也是基于预先处理原数组,然后使用一个额外的Table存储指定query的值得方式。
首先我们定义
M
i
,
j
M{_i}{_,}{_j}
Mi,j,来表示子数组
A
[
i
.
.
.
i
+
2
j
−
1
]
A[i...i + 2^j-1]
A[i...i+2j−1]的最小值的index(从这里可以看到当
j
=
0
j=0
j=0时,表示就是A[i]这一个数组单元),如下图所示。任何关于子数组的query都可以通过两个
M
i
,
j
M{_i}{_,}{_j}
Mi,j覆盖。例如
A
[
2...8
]
A[2...8]
A[2...8]就可以由
A
[
2...5
]
A[2...5]
A[2...5],亦即
M
2
,
2
M{_2}{_,}{_2}
M2,2,和
A
[
5...8
]
A[5...8]
A[5...8],亦即
M
5
,
2
M{_5}{_,}{_2}
M5,2覆盖。所以求一个子数组最小值的问题就转化成为求两个预先存储好两个值的最小值的问题。
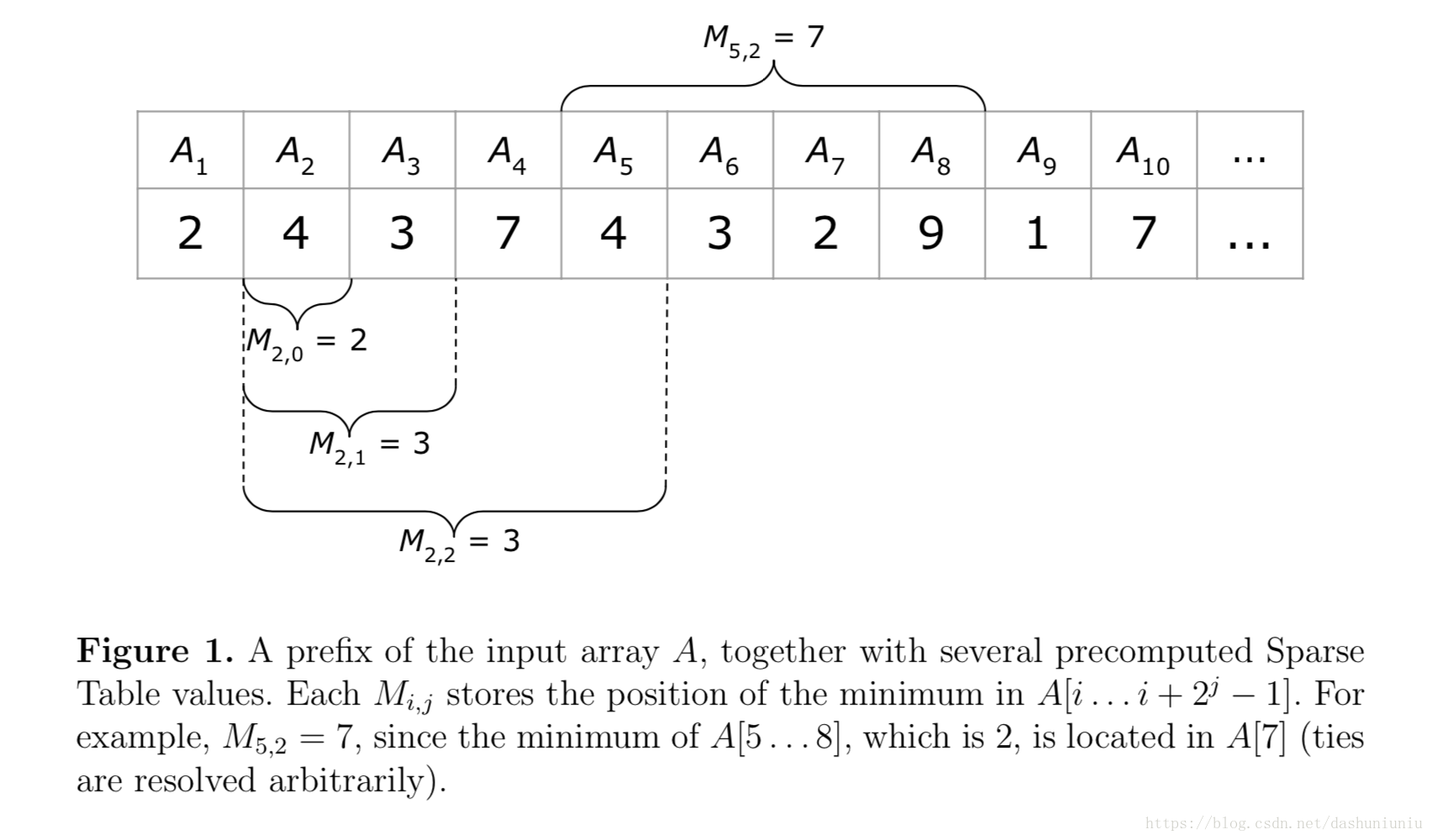
注:该图摘于《Faster range minimum queries》
由于对于数组中的元素 i i h i{_i}{_h} iih而言,都有 l o g 2 n log_2n log2n个值要存储,所以
- 空间复杂度为 O ( n ∗ l o g 2 n ) O(n * log_2n) O(n∗log2n)
- 查询时间复杂度为 O ( 1 ) O(1) O(1)
- 预处理复杂度,使用动态规划来计算的话,复杂度也是 O ( n ∗ l o g 2 n ) O(n * log_2n) O(n∗log2n)
下面我们给出,这个
O
(
n
∗
l
o
g
2
n
)
O(n * log_2n)
O(n∗log2n)空间复杂度的动态规划算法。根据上面
M
i
,
j
M{_i}{_,}{_j}
Mi,j的定义,转移方程如下:
M
i
,
j
=
{
M
i
,
j
−
1
i
f
A
[
M
i
,
j
]
<
=
A
[
M
i
+
2
j
−
1
,
j
−
1
]
M
i
+
2
j
−
1
,
j
−
1
M{_i}{_,}{_j} = \begin{cases} M_{i, j-1} \qquad if A[M_{i,j}] <= A[M_{i + 2^{j-1}, j-1}] \\ M_{i+2^{j-1}, j-1} \end{cases}
Mi,j={Mi,j−1ifA[Mi,j]<=A[Mi+2j−1,j−1]Mi+2j−1,j−1
注:示例数组是从下标1开始的
例如我们要计算
M
2
,
2
M_{2, 2}
M2,2,首先计算得到
M
2
,
1
=
3
M_{2, 1} = 3
M2,1=3,
M
4
,
1
=
5
M_{4,1} = 5
M4,1=5,然后
A
[
3
]
<
A
[
5
]
A[3] < A[5]
A[3]<A[5],所以
M
2
,
2
=
M
2
,
1
=
3
M_{2,2} = M_{2,1} = 3
M2,2=M2,1=3。
然后介绍一下,给定一个查询 R M Q A ( l , r ) RMQ_A(l, r) RMQA(l,r),如何计算出能够覆盖该子数组 A [ r . . . l ] A[r...l] A[r...l]的两个已经存储好的区间。例如我们想要求出 A [ 2...8 ] A[2...8] A[2...8]的最小值,那么首先这个区间长度为 i t h . . . j t h = 6 i_{th}...j_{th} = 6 ith...jth=6的区间,是否能被一个 2 m 2^m 2m覆盖,如果不能的话,肯定能被两个 2 m − 1 2^{m-1} 2m−1覆盖。所以,我们首先求 ⌊ l o g 2 ( j − i ) ⌋ \lfloor log_2(j - i) \rfloor ⌊log2(j−i)⌋,也就是求 l o g 2 ( j − i ) log_2(j-i) log2(j−i)的下取整,假设这个值为k,那么分别
- 从 A [ i ] A[i] A[i]开始取长度为 2 k 2^k 2k的子数组。也就是 M i , k M_{i, k} Mi,k
- 从 A [ j − 2 k ] A[j - 2^k] A[j−2k]开始,长度为 2 k 2^k 2k的数组。也就是 M j − 2 k , k M_{j-2^k,k} Mj−2k,k
如下图所示。
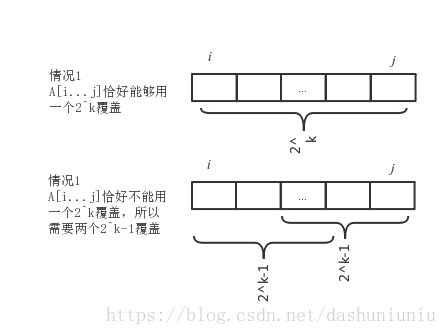
这个算法是2000年由《The LCA Problem Revisited》文章给出,但是并没有过多介绍关于该算法的其它问题,例如我最关心的核心问题
- 为什么使用以2为底,以3或者以4为底是否可行?
Why 2?
首先需要注意的是,基于Sparse Table(狭义)的方式,对于数组 A [ N ] A[N] A[N]而言,最少也要需要存储 N N N个值,或者 N N N个下标。如果存储 N N N个值,在我们需要求 A [ i . . . j ] A[i...j] A[i...j]最小值的时候,就需要遍历这N个值,此时就退化成了查询时间为 O ( N ) O(N) O(N)的情况了。
在最开始的时候,我们使用 M i , j M_{i,j} Mi,j表示 A [ i . . . i + 2 k − 1 ] A[i...i + 2^k - 1] A[i...i+2k−1]的最小值,此时的空间复杂度是 O ( n ∗ l o g 2 n ) O(n * log_2n) O(n∗log2n),如果我们不使用2作为底,而是用3作为底呢?例如我们假设 M i , j M_{i,j} Mi,j表示 A [ i . . . i + 3 k − 1 ] A[i...i+3^k-1] A[i...i+3k−1]的最小值,此时的空间复杂度为 O ( n ∗ l o g 3 n ) O(n * log_3n) O(n∗log3n),是否可行?
底为3也是可行的,但无法在 O ( 1 ) O(1) O(1)时间内完成一次查询。例如我们要取 A [ i t h . . . . j t h ] A[i_{th}....j_{th}] A[ith....jth]的最小值,与2为底的时候相同,我们同样要计算 k = ⌊ l o g 2 ( j − i ) ⌋ k = \lfloor log_2(j - i) \rfloor k=⌊log2(j−i)⌋,只是在如下情况下需要不只一次比较。如下图所示,如果我们要取 A [ 4...11 ] A[4...11] A[4...11],那么取 k = 1 k = 1 k=1,此时无法完全覆盖 A [ 4...11 ] A[4...11] A[4...11],而取 k = 2 k = 2 k=2时,则超出了整个子数组。在我们取 k = 1 k = 1 k=1时,需要比较 A [ M 4 , 1 ] A[M_{4, 1}] A[M4,1], M 7 , 0 M_{7,0} M7,0, A [ M 8 , 0 ] A[M_{8,0}] A[M8,0]和 A [ M 9 , 1 ] A[M_{9,1}] A[M9,1]四个值大小,4个值最少也需要三次比较。
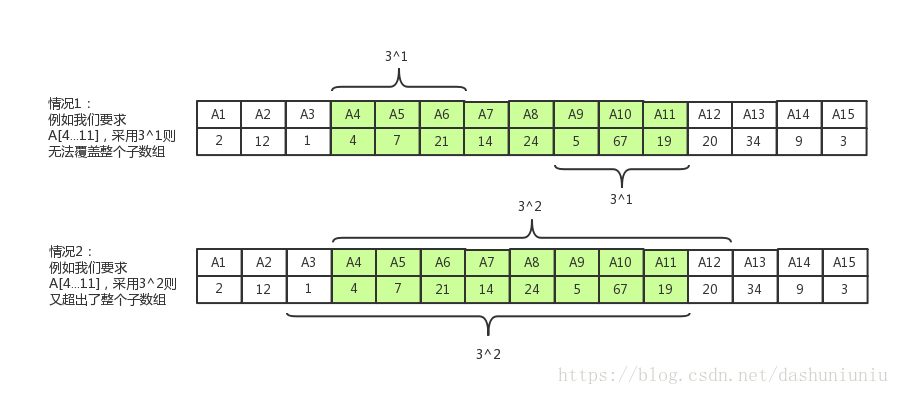
- 空间复杂度为 O ( n ∗ l o g 3 n ) O(n * log_3n) O(n∗log3n)
- 查询时间复杂度为 O ( 1 ) O(1) O(1),无论如何都需要三次比较
- 预处理复杂度,使用动态规划来计算的话,为 O ( n ∗ l o g 3 n ) O(n * log_3n) O(n∗log3n)
那么为什么底为2的时候查询时间复杂度为 O ( 1 ) O(1) O(1),底为3的时候最坏的查询时间复杂度就为 O ( 3 ) O(3) O(3)呢?假设底为 m m m,当长度为 m k + 1 m^{k+1} mk+1的子数组不能由两个 m k m^k mk表示时,无论如何都需要其它值来补充,最坏情况下需要进行关于 2 ∗ ( m − 1 ) 2*(m-1) 2∗(m−1)值的比较。
m k + 1 = m k ∗ ( m − 1 ) + m − 1 m^{k+1} = m^k * (m - 1) + m-1 mk+1=mk∗(m−1)+m−1
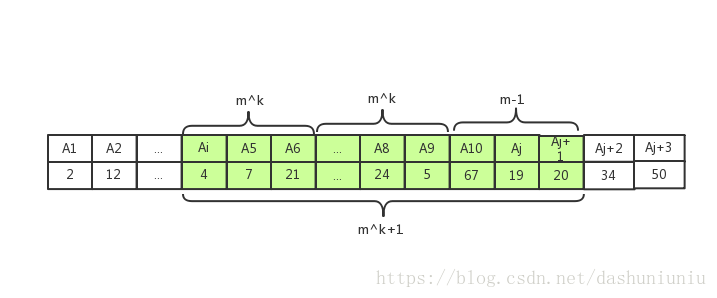
泛化形式
下面我们提出狭义sparse table的泛华形式,取m为底,定义 M i , j M_{i, j} Mi,j为子数组 A [ i . . . i + m j − 1 ] A[i...i+m^j-1 ] A[i...i+mj−1]的最小值,如果我们想要查询 R M Q A ( l . n ) RMQ_A(l. n) RMQA(l.n),我们首先计算 k = ⌊ l o g m n ⌋ k = \lfloor log_mn\rfloor k=⌊logmn⌋,然后取下面两个值:
- 子数组 A [ i . . . i + m k − 1 ] A[i...i+m^k-1] A[i...i+mk−1]的最小值,也就是 M i , k M_{i,k} Mi,k
- 子数组 A [ j − m k + 1... j ] A[j-m^k+1...j] A[j−mk+1...j]的最小值,也就是 M j − m k + 1 , k M_{j-m^k+1,k} Mj−mk+1,k
然后再枚举这两个子数组无法覆盖的中间子数组,然后遍历这个子数组, M i , k 以 及 M j − m k + 1 , k M_{i,k}以及M_{j-m^k+1,k} Mi,k以及Mj−mk+1,k得到最小值,这些值在最坏情况下有 ( m − 1 ) + 2 (m-1) + 2 (m−1)+2个,最少也需要m次比较。此时:
- 空间复杂度为 O ( n ∗ l o g m n ) O(n * log_mn) O(n∗logmn)
- 查询时间复杂度为 O ( m ) O(m) O(m)
- 预处理的复杂度为 O ( n ∗ l o g m n ) O(n*log_mn) O(n∗logmn)
注意对于数组 A [ N ] A[N] A[N]而言,当取底为 N N N时,就相当于将原有数组拷贝了一遍作为sparse table,此时空间复杂度为 O ( N ) O(N) O(N),而查询时的时间复杂度也为 O ( N ) O(N) O(N)。
-------------------------------留坑----------------------------
RMQ在信息论中的极限
Segment Tree
RMQ为什么能够解决LCA问题
Euler Tour
RMQ与Tarjan的区别
ToDo: PAT(Patricia Tree)、Suffix-Tree
[1]: https://www.topcoder.com/community/competitive-programming/tutorials/range-minimum-query-and-lowest-common-ancestor/
[2]: https://blog.youkuaiyun.com/dashuniuniu/article/details/78634002
[3]: https://en.wikipedia.org/wiki/Range_minimum_query
[4]: https://zhuanlan.zhihu.com/p/30248914
[5]: https://stackoverflow.com/questions/3279543/what-is-the-copy-and-swap-idiom
[6]: https://www.geeksforgeeks.org/range-minimum-query-for-static-array/
[7]: https://www.geeksforgeeks.org/sqrt-square-root-decomposition-technique-set-1-introduction/
[8]: https://www.geeksforgeeks.org/range-minimum-query-for-static-array/
[9]: The LCA Problem Revisited








 本文深入探讨了范围最小查询(RMQ)的概念及其在计算机科学中的重要性,包括RMQ的基本定义、朴素解法、动态规划优化、块基表和稀疏表等高级技术。文章还分析了RMQ在LCA问题求解中的应用,以及不同底数对查询效率的影响。
本文深入探讨了范围最小查询(RMQ)的概念及其在计算机科学中的重要性,包括RMQ的基本定义、朴素解法、动态规划优化、块基表和稀疏表等高级技术。文章还分析了RMQ在LCA问题求解中的应用,以及不同底数对查询效率的影响。
















 462
462

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








