贪心算法-- 0-1背包问题求解及思路

贪心算法是一种只考虑眼前利益的思路，不全盘考虑问题的所有可能，每一步做出当时看起来最佳的选择(局部最优选择)

给定n种物品和一个背包。物品i的重量是Wi，其价值为Vi，背包最大承载重量为C。假设物品是不可分割的，应如何选择装入背包的物品，使得装入背包中物品的总价值最大?

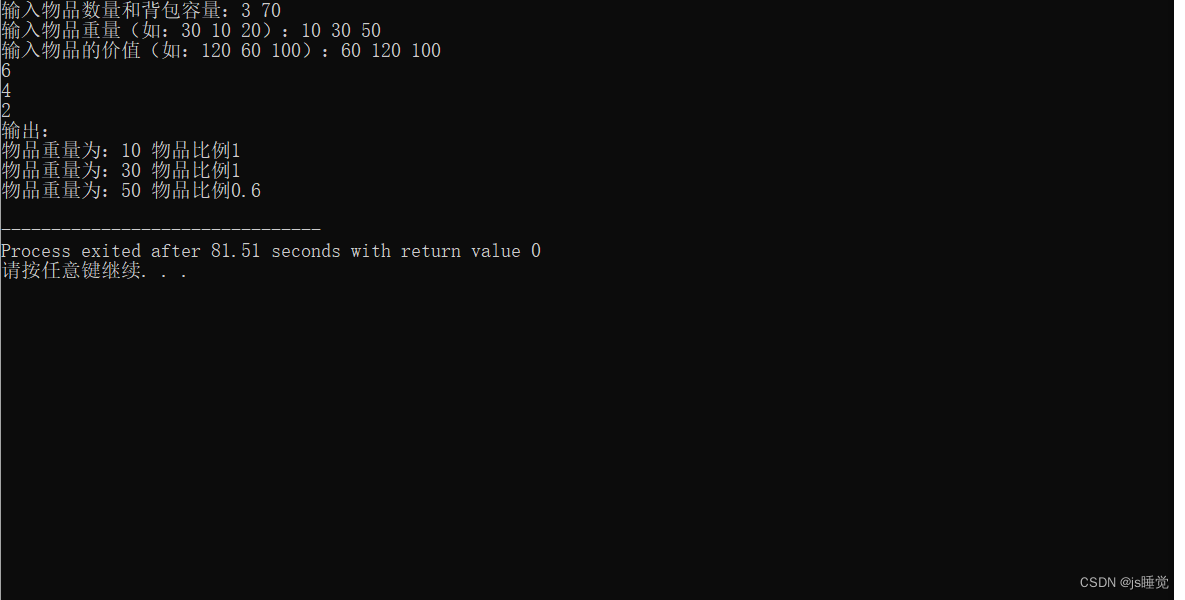
 花瓶：10公斤 60w      屏风：30公斤 120w   砚台：20公斤 100w

首先我们按照物品的单位重量价值来进行排序，然后按照单位重量价值从高到低依次进行选择，若其能装入背包则将其装入，不能则继续判断下一个直至所有物品都判断完，就得到了问题的一个解。但是对于0-1背包问题贪心算法并不能保证背包全部空间被利用因此背包的单位物品价值就会变低 因此0-1背包问题利用贪心算法并不能求得最优解。

代码如下：

#include<bits/stdc++.h>
using namespace std;
void Sort1(int n,double w[],double v[]){
    int max1;
    double t[20];
    for(int i=1;i<=n;i++){
        t[i]=v[i]/w[i];
        //cout<<t[i]<<endl;
    }
    for(int i=1;i<=n;i++){
        max1=i;
        for(int j=i+1;j<=n;j++){
            if(t[j]>t[max1]){
                max1=j;
            }
        }
        swap(t[i],t[max1]);
        swap(w[i],w[max1]);
        swap(v[i],v[max1]);
    }
    for(int i=1;i<=n;i++){
        cout<<t[i]<<endl;
    }
}
//n为物品数量，c为背包最大容量，w[]为物品重量，v[]为物品价值，b[]为背包存放 
void knapsack_greedy(int n,double c,double w[],double v[],double b[]){
    int j;
    //Sort1(n,w,v);
    Sort1(n,w,v);
    for(int i=1;i<=n;i++)//初始化背包b[]
        b[i]=0;
    for(j=1;j<=n;j++){
        if(c<w[j]) break;
        b[j]=1;
        c=c-w[j];
    } 
    if(j<=n)
        b[j]=c/w[j];
    cout<<"输出："<<endl;
    for(int i=1;i<=n;i++){
        cout<<"物品重量为："<<w[i]<<" "<<"物品比例"<<b[i]<<endl;
    }
}
int main(){
    int n,c;
    double b[20],w[20],v[20];
    cout<<"输入物品数量和背包容量：";
    cin>>n>>c;
    cout<<"输入物品重量（如：30 10 20）："; 
    for(int i=1;i<=n;i++)
        cin>>w[i];
    cout<<"输入物品的价值（如：120 60 100）："; 
    for(int i=1;i<=n;i++)
        cin>>v[i];
    knapsack_greedy(n,c,w,v,b);    
    return 0 ;
}