当你拉伸一条橡皮筋时,它会明显变细边长,我们测量下其未拉伸时的长度(L0)和直径(D0),然后测量下拉长变形量ΔL和直径变化Δd,将(ΔL/L0)比(Δd/D0),即得到了泊松比υ,材料的泊松比是表征材料变形特性的一个重要参数,上述例子我们介绍了其定义为:材料受到单轴应力时:横向应变/纵向应变的负数(早期科学家还没有发现拉伸时膨胀的材料,故加负号以使之为正,便于使用),那么同学们你有没有想过,为什么不是用纵向的应变/横向的应变,而是反过来呢?
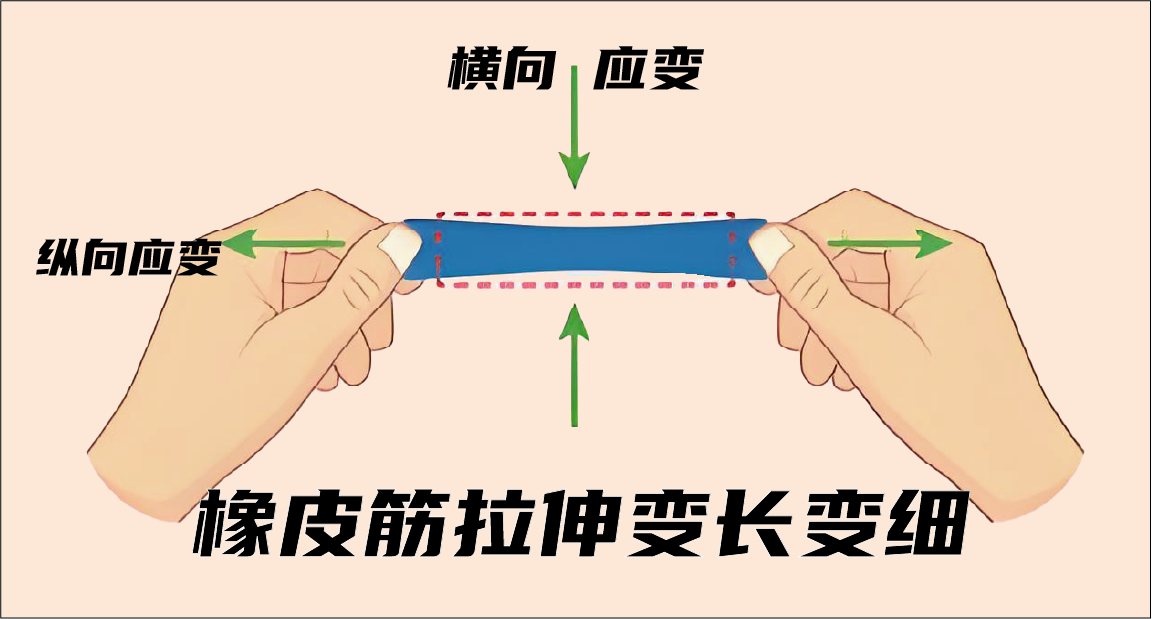
有同学会说泊松定义的泊松比就是这样的,但是为什么泊松不定义一个反过来的参数呢?带着小朋友的疑问,达芬奇探索了一下,发现泊松定义这个参数背后综合了工程、物理及数学上的实际考量,而不是简单的数学变形量之比。

从历史起源上说,西莫恩·德尼·泊松(Simeon Denis Poisson)所在年代的科学家更关注材料在单一方向受力后在其他方向上的响应,如在纵向拉伸时,横向变形情况;因为早期实验,科学家能够最直观观察测量到横向收缩量。横向应变是应力作用下的“被动结果”,纵向应变为原因,科学家关注在应力作用下的变形结果,故将其“被动结果”置于分母,“主动原因”纵向应变置于分子,符合当时科学家的研究对比便利性和人的直观性理解。
从物理意义上说泊松比表示在材料收到纵向拉伸时,横向的变形程度,若反过来,物理含义应该是单位横向变形量下的纵向变形量,这个概念本身是没有问题的,但是物理概念的定义是为了解决实际问题的需要才提出的,在实际工程中,我们遇到的很多问题都是明确纵向受力,求解横向变形量:比如在设计桥梁时,确定一根钢索承受的拉力,求其直径变化量;通过已知材料的泊松比可以很方便的计算出横向变形;在建筑物设计中,通过计算粘土的受压时的横向膨胀变形来加固减少不均匀沉降,计算桩基结构等。在航空航天领域,工程师会保证在受到外力作用时,横向变形相对较小,才利于保持结构的稳定性和完整性,确保飞机在飞行过程中的安全性。而泊松比能帮助快速计算出材料横向收缩或膨胀的程度,从而优化结构设计。
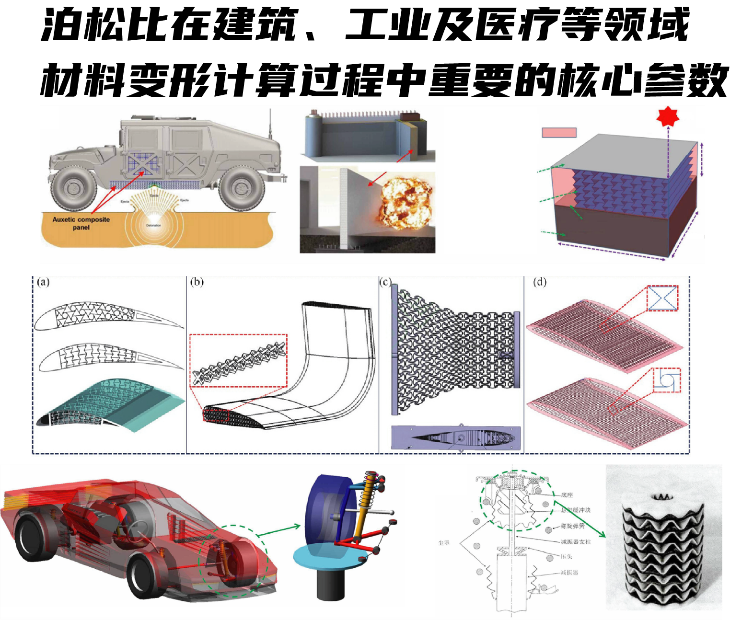
再退一步讲,假设你一定要这样创造这样的使用场景,比如上面提到的轴,我要想知道轴直径变化单位量下的长度变形量,我们完全可以通过将现有轴横向变形定义为纵向应变,从而求得横向。如果泊松比定义为纵向/横向,公式中将频繁出现倒数(1/υ),既然实际需求用的多,我们不应该在物理上再创造障碍一直用倒数,这不是增加复杂度吗😧。
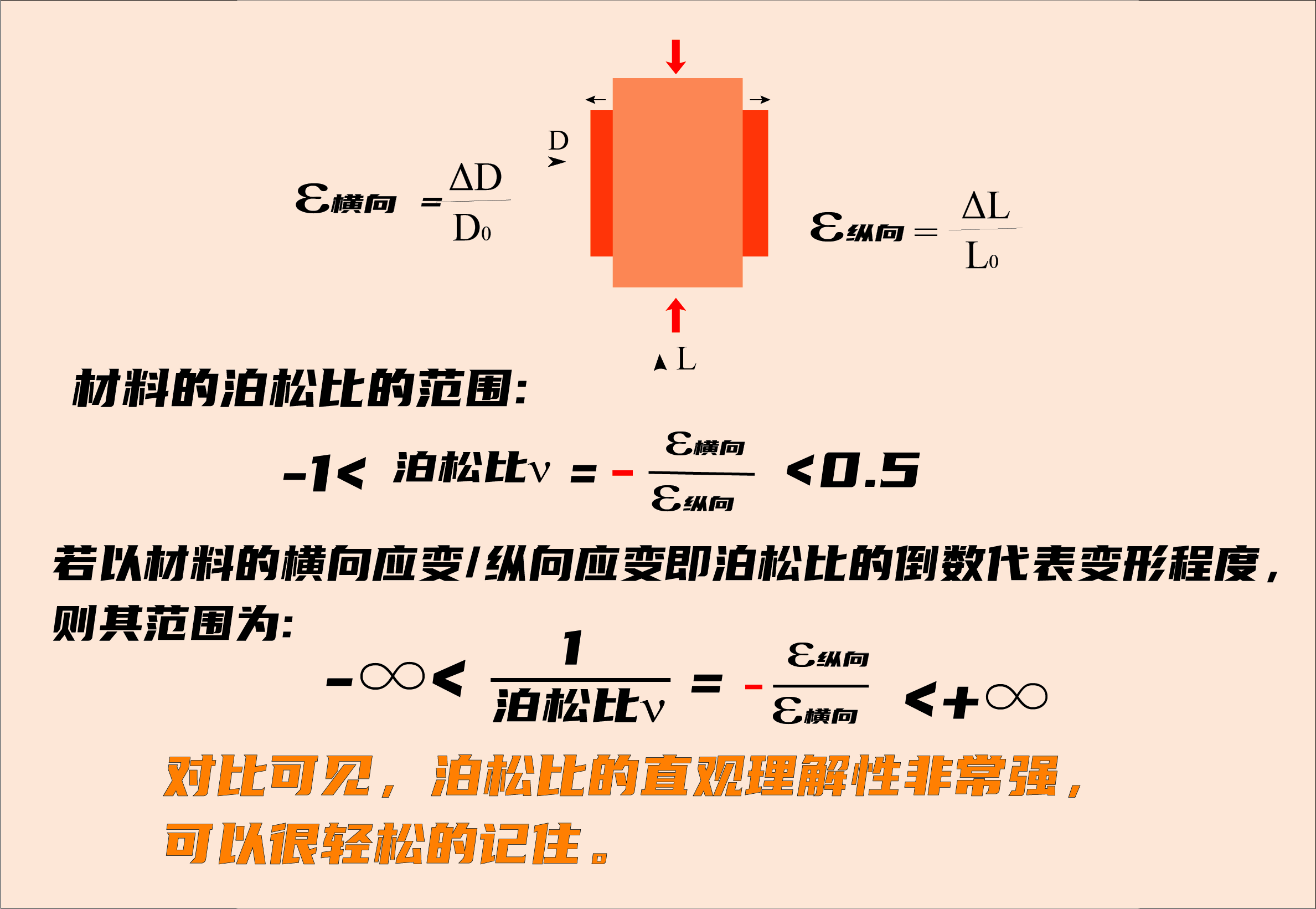
另外从数学角度,泊松比υ的取值范围通常为-1~0.5,常见材料的横向变化量都会小于纵向变形量,当材料的横向变形量很小,如接近0时,横向/纵向变形的取值会非常大,取值范围从负无穷至正无穷,对于日常使用将会非常不方便;而泊松比-1到0.5的取值范围,直观理解性就会非常强,我们可以很轻松的记住常见的材料的泊松值,如当泊松比υ =0.5时,材料不可压缩(如橡胶),体积变化为0;常见金属材料的泊松比范围为:0.2~0.35;软木的泊松比接近0,横向几乎不变形;而1987年才发现的负泊松比材料如某些多孔聚合物泡沫的材料最小值可以达到-1。
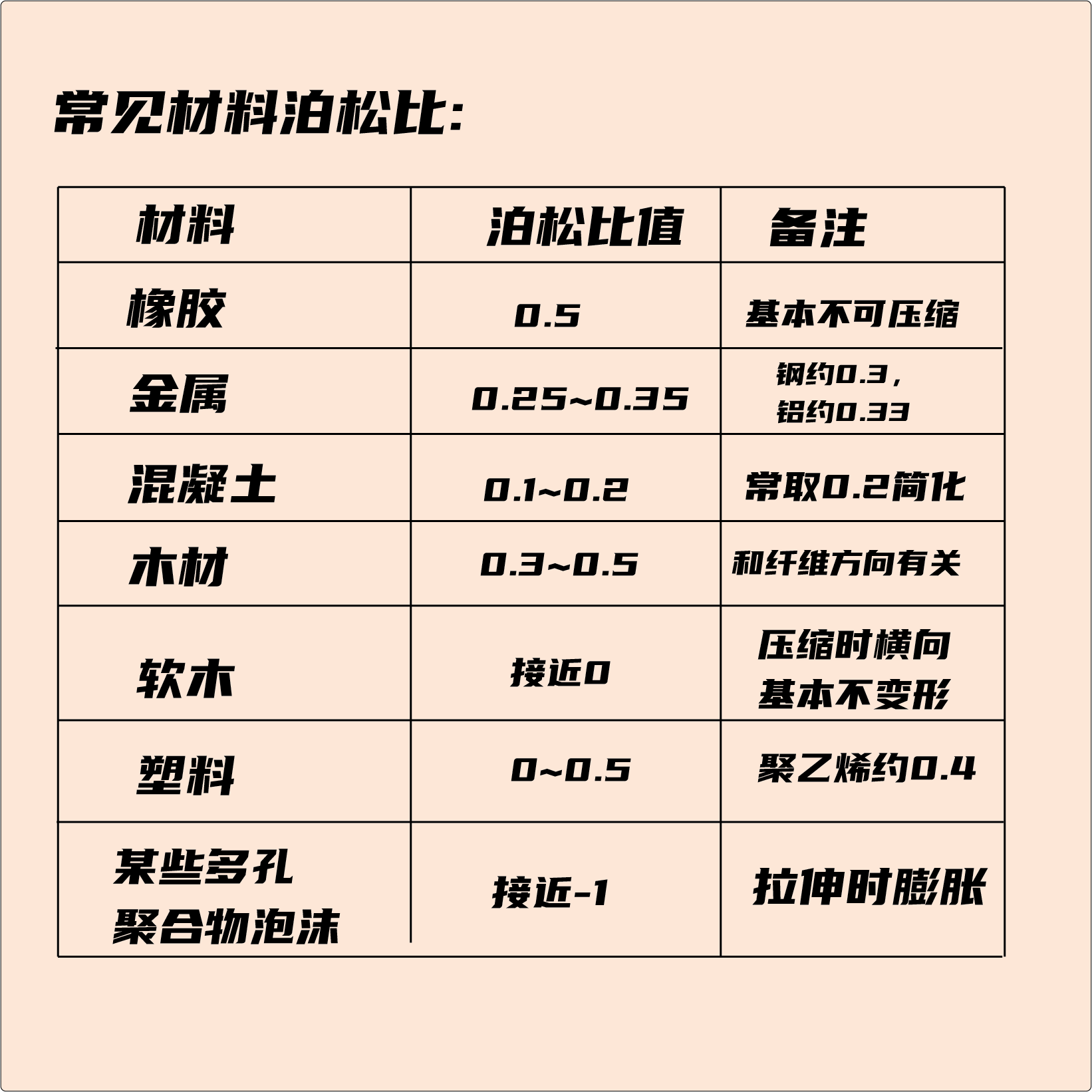
综上,从历史渊源、物理意义及实际工程需要和数学角度都说明,泊松定义泊松比的含义是综合了多方面的考虑。从中我们也应该看到,一个看似随意的定义,其背后蕴含的科学原理也是将来我们作为新世纪的概念定义人应该借鉴学习的。

























 1356
1356

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








