MATLAB函数回归调用，你真的理解吗？

最新推荐文章于 2025-12-02 19:45:00 发布

原创最新推荐文章于 2025-12-02 19:45:00 发布 · 180 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#matlab

文章讨论了一段用最小二乘法估计指数函数e^x-10根的代码问题，原始代码存在无法正确打印结果的问题。作者分析了阶乘函数的递归调用机制，并提出了一种改进的迭代方法，通过误差裕度控制循环次数来避免无限递归，最终找到根的近似值。修改后的代码能有效解决原问题。

写了一个最小二乘法估计EXP（x)-10的根代码，发现打印不出最后的值。

multi(0,3)
function m=multi(a,b)
m=(a+b)/2
if b-a<0.01
    return 
end
if (exp(a)-10)*(exp(m)-10)<0
    multi(a,m)
end
if (exp(m)-10)*(exp(b)-10)<0
    multi(m,b)
end

end

然后看了一下阶乘的回归调用内部原理

function y=fac(n); 
if n<0 
 error('n is smaller than 0,error input.'); 
 return; 
end 
if n==0|n==1 
 y=1; 
else 
 y=n*fac(n-1); 
disp(y)
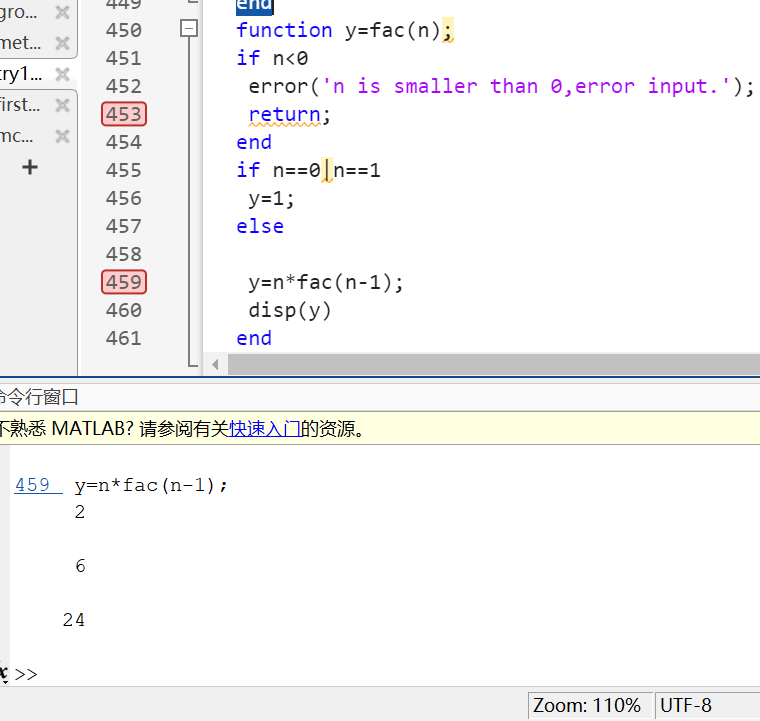
end

debug可知，程序在第9行会一直调用自己4次而无Y值打印出来，然后才会出来，在9 10 11行之间再次循环绕出到最外一层，打印值依次为2 6 24 125，看出来了吧，打个比方，回调就是一个环形迷宫，调用一次就深入一层，直到结束调用，又一层一层出来回复到最初那一层。

所以该进方法为：

function m=multi(x1,x2)
while x2-x1>0.001%误差裕度控制循环次数
if (exp(x1)-10)*(exp((x2+x1)/2)-10)<0
x2=(x1+x2)/2
end
if (exp(x2)-10)*(exp((x2+x1)/2)-10)<0
x1=(x1+x2)/2
end
end
m=x1
end