MATLAB欧拉法

最新推荐文章于 2023-08-06 22:50:01 发布
最新推荐文章于 2023-08-06 22:50:01 发布
阅读量2k 收藏 19
点赞数 6
CC 4.0 BY-SA版权
文章标签： matlab
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/dadashibangwa/article/details/128705526
文章讨论了在MATLAB中，使用函数句柄直接调用函数与通过feval的等效性，特别是在解决矩阵特征值问题上的例子。此外，还涉及到了龙格库塔法在常微分方程求解中的应用，强调了迭代次数、步长对计算时间和精度的影响，以及一阶线性近似导致的误差。提到优化方法是通过对比不同设置来寻找最佳解法。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

  • 如果您有函数句柄，不需要使用 feval，因为您可以直接调用函数句柄。以下语句的结果是相等的。

fh = @eig;

[V,D] = fh(A)

[V,D] = feval(@eig,A)

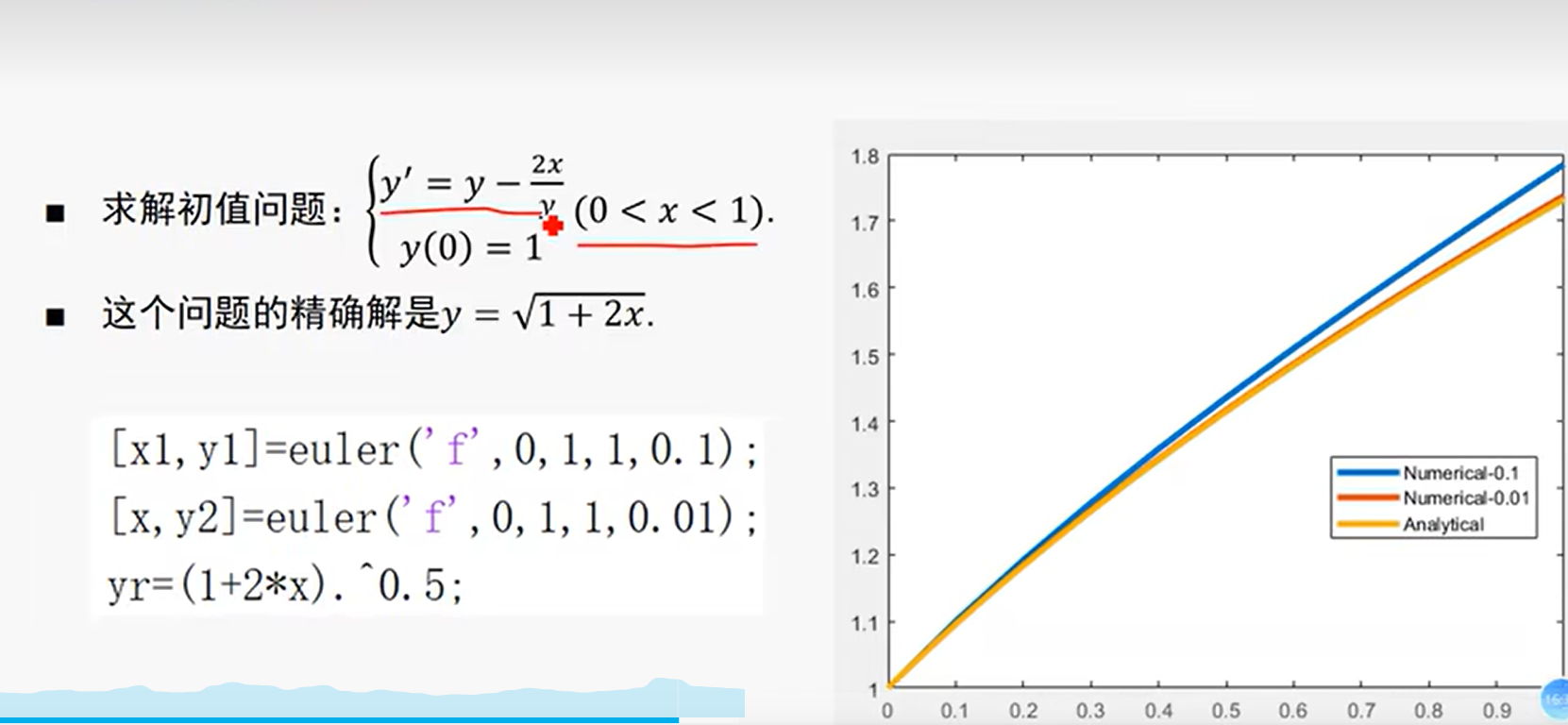
迭代次数分别为0.1和0.01的情况，次数越多，时间越长

此时控制变量为步长均为0.1

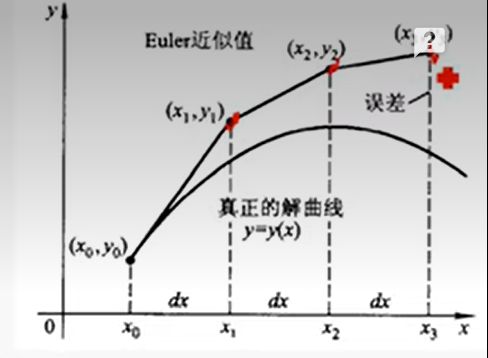
一阶线性近似，舍去^2项，故误差是h^2

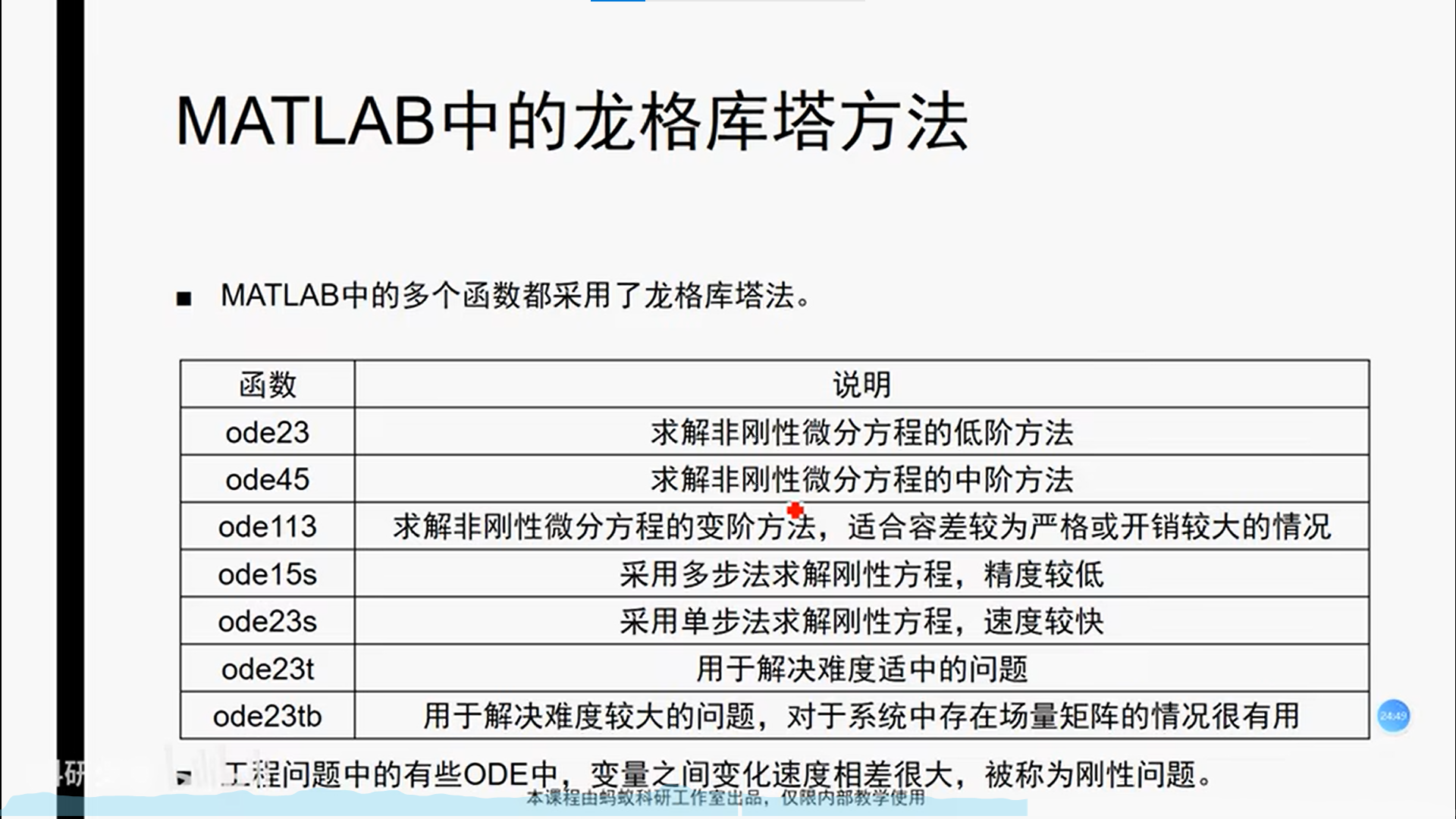
最好的方法是全部代一遍，看哪个最符合要求，只需要知道，龙格库塔法是通过多次求斜率取均值提升准确度的，且他们是ODE方程：常微分方程(ordinary differential equation)的解法

求解的微分方程的自变量可以有很多，但是只能对其中一个龙格库塔法

蕙兰之韧
关注
欧拉方法：欧拉方法：的matlab程序
10-23
里面含有欧拉方法：欧拉方法：的MATLAB程序 经过了matlab 的验证 绝对是对的 请大家放心下载
matlab欧拉法程序,欧拉法matlab程序.doc
weixin_42356284的博客
03-17 3882
欧拉法matlab程序.doc 1.Euler法function[x,y]=naeuler(dyfun,xspan,y0,h)x=xspan(1):h:xspan(2);y(1)=y0;forn=1:length(x)-1y(n+1)=y(n)+h*f(dyfun,x(n),y(n));endx=x ;y=y ;x1=0:0.2:1;y1=(1+2*x1).^0.5;plot(x,y,x1,y1)...
matlab的欧拉方法代码-Euler-s-Method:欧拉法
05-26
matlab的欧拉方法代码欧拉法 包含用于使用Euler方法和Modified Euler方法求解一阶ODE的代码。 理查森的外推法用于达到更高的精度要求。 所有代码都是使用Matlab的文件扩展名.m为Matlab编写的
matlab 显示欧拉法,[MATLAB数学相关] 显示欧拉法的问题
weixin_42511080的博客
03-29 717
显示欧拉法的问题 题目：dy=-y+x+1 y(0)=1 h=0.1用显示欧拉法 【y(i+1)=y(i)+h*(-y(i)+x(i)+1)】 求解我的结果如下：为什么误差不一直增大？？X Y 精解 误差0 1.0000 1.0000 00.1000 1.0000 1.0048...
MATLAB使用欧拉Euler法求解微分方程组
04-24
MATLAB使用欧拉Euler法求解微分方程组 部分源码 clear;clc c=2/3; %设置c的值 x(1)=0.1; %设置x初值为0.1 y(1)=0.3; %设置y初值为0.3 h=0.05; %设置步长为0.05
欧拉法：数值微分欧拉法的Matlab代码-matlab开发
05-29
欧拉法是一种求解给定初值的一阶一阶微分方程的数值方法。 它是对常微分方程进行数值积分的最基本的显式方法，并且是最简单的Runge–Kutta方法。 欧拉法是一阶方法，即局部误差（每步误差）与步长的平方成正比，全局...
数值分析欧拉法、改进的欧拉法、4阶龙格库塔法 MATLAB算法
04-13
数值解与理论解对比可知，四阶龙格-库塔法的精度已经很高，用它来解一般常微分方程已经足够了。 有程序运行说明 数值解与理论解对比可知，四阶龙格-库塔法的精度已经很高，用它来解一般常微分方程已经足够了。...
MATLAB实现欧拉法求解常微分方程组.zip
02-29
在MATLAB环境中，常微分方程（ODEs）的数值解是通过各种数值方法来获得的，其中欧拉法是一种简单且基础的方法。本文将详细介绍如何使用MATLAB实现欧拉法来求解常微分方程组，以及提供的EulerMethod.m和f.m文件在该...
"船舶无人驾驶技术研究：基于Nomoto响应型操纵运动的线性仿真程序与回转、Z型实验的MATLAB实现（欧拉法）","无人船操纵运动仿真：基于线性Nomoto响应模型的回转与Z型实验MATLAB欧拉法
02-11
"船舶无人驾驶技术研究：基于Nomoto响应型操纵运动的线性仿真程序与回转、Z型实验的MATLAB实现（欧拉法）","无人船操纵运动仿真：基于线性Nomoto响应模型的回转与Z型实验MATLAB欧拉法程序设计与分析",船舶 无人艇 ...
【气动学】基于matlab欧拉法+龙格库塔算法火箭飞行弹道仿真【Matlab仿真 8834期】.zip
12-20
优快云 Matlab武动乾坤上传的资料均有对应的仿真结果图，仿真结果图均是完整代码运行得出，完整代码亲测可用，适合小白； 1、完整的代码压缩包内容 主函数：main.m； 调用函数：其他m文件；无需运行 运行结果效果图；...
MATLAB使用欧拉Euler法求解微分方程组 源程序代码
04-03
MATLAB使用欧拉Euler法求解微分方程组 源程序代码
改进欧拉法matlab程序
07-06
改进欧拉法的MATLAB程序，适合初学者使用的程序，简单易懂
matlab的欧拉方法代码-Generic_Code_Euler_Method:此代码是用MATLAB编写的，用于Euler方法
05-26
matlab的欧拉方法代码Generic_Code_Euler_Method 此代码是用MATLAB编写的，用于Euler方法 非正式的几何描述 考虑计算从给定点开始并满足给定微分方程的未知曲线的形状的问题。 在这里，可以将微分方程视为公式，一旦计算出该点的位置，便可以通过该公式计算曲线上切线的斜率。 这个想法是，尽管曲线最初是未知的，但它的起点（我们用{\ displaystyle A_ {0}，} A_ {0}表示）是已知的（请参见右上图）。 然后，根据微分方程，可以计算出{\ displaystyle A_ {0}} A_ {0}处曲线的斜率，因此也可以计算出切线。 沿着该切线到点{\ displaystyle A_ {1}。} A_ {1}，走一小步。 沿着这一小步，斜率不会发生太大变化，因此{\ displaystyle A_ {1}} A_ {1}将接近曲线。 如果我们假装{\ displaystyle A_ {1}} A_ {1}仍在曲线上，则可以使用与上面的点{\ displaystyle A_ {0}} A_ {0}相同的推理。 经过几个步骤，计算出多边形曲线{\ d
matlab的欧拉方法代码-Schroedinger_PDEs:Schroedinger_PDEs
05-26
matlab的欧拉方法代码SchrödingerPDE：数值解和模拟。 作者：AlejandroGalván，Daniel Quiles和Bernat Ramis-UPC数学和工程物理专业的学生。 这项工作的目的是研究数值方法求解Schrödinger偏微分方程的适用性。 我们从开发一维方程的两个离散版本开始：第一个根据Euler方法，而第二个使用更稳定的Crank-Nicolson方法。 后来，我们还推导了二维空间情况下的Crank-Nicolson方程。 在Matlab中实现这些方法后，我们开始对一些简单的量子系统进行建模。 随着我们获得的模拟完全符合其背后的理论，我们转向了更困难或非常规的系统，以期希望找到更多有趣的结果，并发现数值PDE求解的优缺点。 该存储库包含一些模拟视频和一个pdf文件，其中对我们的工作方法进行了详尽的说明，并附带了我们所实现的代码的附录。
欧拉法解常微分方程组数值解的MATLAB程序
05-25
用Eular法解常微分方程组的数值解，使用了细胞数组，代码简洁，除注释外的有效代码只有二十行左右。（几年前上传的程序了，当时要20积分，现在为大家降到5个积分）
实验十.欧拉法MATLAB实现
智多星736的博客
12-01 5768
数学建模实验报告：欧拉法MATLAB实现
40.利用欧拉法求解微分方程组（matlab程序）
m0_57943157的博客
08-06 2110
求解微分方程的时候，如果不能将求出结果的表达式，则可以对利用数值积分对微分方程求解，获取数值解。title('time evolution plot') %设置图形的标题。xlabel('time') %设置x轴的标签。ylabel('value') %设置y轴的标签。legend({'x','y'}) %设置图例。plot(t,x) %绘制x曲线。plot(t,y,'r') %绘制y曲线。xlabel('x') %设置x轴的标签。ylabel('y') %设置y轴的标签。
欧拉法(Euler)求解常微分方程的Matlab程序及案例
热门推荐
Matlab_Fans技术博客
02-28 5万+
文章目录1. 概念1) 常微分方程2) 一阶常微分方程3) 微分方程的解析解法和数值解法2. 算法2.1 显式欧拉法2.2 隐式欧拉法2.3 两步欧拉法2.4 改进欧拉法2.5 四种欧拉方法的对比3. 程序4. 案例5. 联系作者 1. 概念 1) 常微分方程 自变量只有一个的微分方程，称为常微分方程；自变量数量2个或以上时，称为偏微分方程。 绝大多数实际工程问题，常微分方程的自变量都是时间t，通常表达为： F(t,y,y˙,⋯ ,y(n−1),y(n))=0F\left( {t,y,\dot y, \cd
显式欧拉格式——matlab实现
CV老李的博客
03-16 8677
日期：2020-3-16 显式欧拉格式 格式为： 我运用显式欧拉格式计算三道例题，然后展现其效果，最后将我的代码展示出来 1. 2. 3. 呈现出这样的曲线的原因是该函数由一开始的极其陡峭变为后来的非常平稳，其中斜率的变化率非常之大。 而欧拉格式走的是直线，在一个步长内斜率是不发生变化的，也就是当这个折线走完一个步长，与真实的曲线之间在数值上已经有很大的差别了。后面随着曲线的陡峭程...
matlab 欧拉法
最新发布
03-12
### 实现欧拉法的 MATLAB 示例 在MATLAB中实现简单的欧拉方法用于求解常微分方程可以通过定义函数并迭代更新来完成。下面是一个具体的例子，演示了如何使用欧拉法解决初值问题 \( y' = f(t, y),\;y(t_0)=y_0 \)[^1]...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值