基于驾驶信息的驾驶员状态检测模型

基于驾驶信息的三种驾驶员状态检测模型开发使用车辆模拟器；正常、疲劳和酒后驾驶

1. 引言

酒后驾驶和疲劳驾驶是导致致命车辆事故的主要因素。当驾驶员处于疲劳状态或醉酒状态时，其对车辆的控制能力会下降。许多研究表明了这两种状态的共同特征和差异。例如，持续清醒至少18小时的影响相当于血液浓度（BAC）达到0.05%的情况（道森和里德，1997；威廉姆森和费耶，2000；阿内特等人，2001）。此外，持续清醒至少24小时的影响相当于血液酒精含量达到0.10%（道森和里德，1997；拉蒙德和道森，1998）。另一方面，张兴健的研究显示，在五种受控情况（正常、疲倦驾驶、疲劳驾驶、困倦+疲倦驾驶和酒后驾驶）下，对二十五名参与者的生理影响表现出差异。结果表明，心率和对光的反应时间是疲劳驾驶员的重要特征。在醉酒状态下，驾驶员的生理特征受到酒后驾驶的影响：收缩压、对光的反应时间、深度偏差感知、视力、对声音的反应时间以及速度预期的时间偏差。特别是，收缩压和深度知觉偏差在醉酒状态与正常状态的回归模型中表现出显著影响（张等人，2014）。

根据美国国家公路交通安全管理局（NHTSA）的估算，2012年有近10,322人死于与酒精相关的交通事故。采用多重插补法估计，2009年至2013年在美国，疲劳驾驶占所有事故的7%，占致命事故的16.5%（特夫特，2014）。此外，根据美国一项全国代表性电话调查，41%的驾驶员承认曾“睡着或打盹”（苏伊特，2010）。

为了防止醉酒和疲劳驾驶，需要开发专业技术。目前有两种方法可用于检测醉酒状态：生理测量方法和基于车辆的测量。

生理测量方法基于生理信号，例如脑电波、肌电图（EMG）、脑电图（EEG）、眼部活动、面部表情等。许多研究发现，可以通过这些方法检测醉酒状态。已开发出一种基于碳纳米管的酒精传感器用于测量血液酒精浓度（Leng林，2010年）。小岛等人（2009）利用这些生理测量方法开发了一种用于检测酒后驾驶的无创系统。萨博酒精锁通过直接测量来检测驾驶员的状态。该设备由萨博开发，包含一个小型吹嘴。如果驾驶员呼出的气体中含有酒精，发动机将无法启动。

在利用生理特征检测困倦状态方面，脑电图（EEG）是检测疲劳驾驶行为最有效的指标之一。它通过测量脑神经元内部离子电流流动产生的电压波动来实现（Niedermeyer 和 da Silva，2005）。肌电图（EMG）是一种记录骨骼肌所产生的电活动的电诊断医学技术，属于驾驶员困倦的生理特征（Fu 和 Wang，2014）。然而，脑电数据中存在大量噪声，在使用前需要予以消除。

通常，基于车辆的测量方法（如横向位置、加速度、方向盘转角等）在现实应用中存在精度低的局限性，因为无法涵盖驾驶过程中的所有情况。然而，随着机器学习算法的发展，这些局限性已得到很大程度的克服。与生理信号方法相比，基于车辆的方法也具有诸多优势（埃斯坎达里安，2012年）。基于车辆的测量无需使用导线和电极连接驾驶员，且处理过程对计算能力的需求较低。此外，采集转向角度和制动踏板等信息所需的硬件少于生理信号的采集。最后，该方法因具备非侵入特性，更易于实现工程化应用。

戴等人（2010年）使用加速度和姿态传感器，通过手机检测酒后驾驶。为了检测醉酒状态，李开发了3种算法，分别采用逻辑回归、决策树和支持向量机（李等人，2010年）。多层感知机（MLP）和支持向量机（SVM）被用于判断血液酒精浓度是否超过0.4克/升（罗比内尔和普曾纳特，2013年）。李等人（2015年）基于车辆模拟器的多元时间序列分类，开发了醉驾检测方法。

赛义德和埃斯坎达里安（2001）成功利用转向角度等驾驶信息，通过人工神经网络（ANN）实现疲劳驾驶检测，尽管该算法的训练数据需要进行预处理工作，例如去除与道路曲率部分相关的驾驶数据。为了提高分类的准确性，克拉耶夫斯基等人（2009）收集了来自12名驾驶员的方向盘数据作为输入，并采用特征提取方法，提取了时域、频域、谱域和状态空间域的特征。他们的混合检测算法达到了86.1%准确率。使用随机森林算法，麦克唐纳的检测方法通过转向角实现了80%准确率（McDonald et al., 2012）。文等人（2012）开发了利用转向角度传感器和车辆模拟器中的车辆信息来检测疲劳状态的算法。王等人（2016）利用车辆模拟器，结合不同时间分辨率和数据集，采用随机森林机器学习算法开发了基于驾驶信息的疲劳行为检测方法。

在先前的研究中，对三种状态（正常、困倦和醉酒）进行全面检测和分类的研究相对较少。尽管对驾驶员安全至关重要，但针对从正常驾驶中检测困倦和酒后驾驶的研究通常是分别进行的，并且检测技术也朝着相同方向发展。此外，构建能够检测醉酒状态的分类系统在自动驾驶汽车中十分必要，因为允许或限制手动操作模式需要准确掌握驾驶员状态。

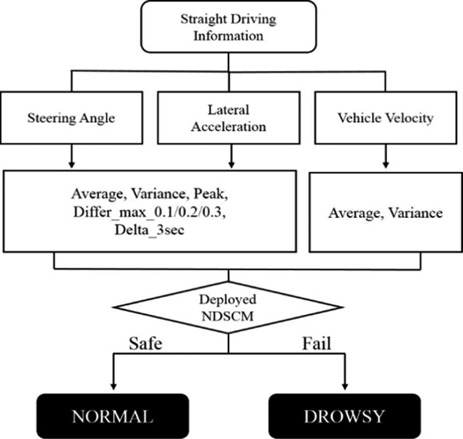
本文通过车辆模拟器在高速公路（SCH）上进行了两种类型的道路状况实验。第一种是在自由道路上以100 km/h的速度行驶，道路上无其他车辆，用于分析困倦、醉酒和正常驾驶之间的差异。第二种是驾驶事件路段，其中包括其他车辆等障碍物以及紧急停车情况。通过这些实验，获取了加速度、速度、踏板压力、转向角和横摆率作为指标。这些变量用于各状态的统计分析，并提出了三种检测算法模型：正常与疲劳状态分类模型（NDSCM）、醉酒与疲劳状态分类模型（DDSCM）以及基于事件的异常检测模型（AMFOE）。NDSCM利用直线道路驾驶数据（转向角、纵向加速度和车辆速度），采用随机森林方法对疲劳和正常行为进行分类，该模型是王的研究的改进模型。DDSCM使用来自车辆的加速度数据，通过机器学习方法（人工神经网络和随机森林）对醉酒和疲劳状态进行分类。最后，AMFOE利用变道数据检测异常行为，该模型基于转向角和横向加速度方差的特定规则。结果表明，由这三种算法模型组成的系统可全面检测驾驶员的三种状态（困倦、醉酒和正常）。

2. 实验环境

真实疲劳驾驶和酒后驾驶是危险且违法的；因此，这些实验采用虚拟驾驶车辆模拟。驾驶模拟器和虚拟驾驶环境被设计用于提高模拟的真实性。框架、座椅和驾驶装置，如方向盘、加速踏板和制动踏板，均已安装，如图1（郑等人，2013）所示。虚拟车辆通过电动车结构构建。使用“MATLAB/SIMULINK”（朴等人，2014）构建的虚拟车辆模型与实车模型进行了比较。该虚拟驾驶实验的有效性得到了验证（郑等人，2013）。虚拟驾驶条件包括从首尔至天安高速公路（SCH）的韩国高速公路路段，总驾驶距离为63.9公里。

十二名年龄在20至30岁的男性使用驾驶模拟器进行这些实验。他们均身体健康，无疾病，拥有2至9年的驾驶经验，身高和体重分别为 176 ± 10厘米和 72 ± 13千克。从起床到实验开始期间，禁止摄入咖啡因或药物，同时禁止剧烈运动和吸烟，以使参与者处于更真实的状态。为预防模拟器晕动症症状，要求他们在实验开始前在驾驶模拟器中进行练习。所有实验均按照机构审查委员会（IRB）认证（IRB证书编号2018‐05‐015‐002）的规定进行。

实时驾驶信息从驾驶模拟器中收集，采样频率为 100赫兹。为了分析和评估驾驶员的状态，记录了面部和驾驶屏幕的视频。

(1) 纵向加速度（m/s²）
(2) 横向加速度（m/s²）
(3) 车速（m/s）
(4) 加速踏板压力（psi）
(5) 制动踏板压力（psi）
(6) 转向角（°）
(7) 横摆率

3. 正常与疲劳状态分类模型（NDSCM）

王等人（2016）使用相同的车辆模拟器开发了疲劳状态检测算法模型。研究表明，采用加速度和转向角的 20秒数据集作为输入对疲劳驾驶行为检测最为有利。然而，该输入参数总数达到60个，导致算法的计算处理速度变慢。此外，它需要20秒数据集进行检测。如果使用4秒数据集，错误率平均为0.31（0.269~0.35）。因此，建议在本部分使用具有更好处理速度和实时操作系统的改进的DNSCA算法。

3.1 正常与疲劳状态的实验条件

为了获取开发疲劳检测算法所需的数据，进行了两种状态下的实验：正常状态和疲劳状态。为获得正常状态的车辆信息，白天驾驶实验在下午12:45至14:45进行。疲劳状态的实验则在凌晨 2:00至4:00进行。这些实验安排的详细信息见表1。每次实验有2名参与者（标记为‘A’和‘B’）。在夜间驾驶实验中，参与者经历了约18~22小时的睡眠剥夺。驾驶员有15分钟的练习时间，以适应正常驾驶状态。他们驾驶于首尔至天安高速公路（SCH），该路段无其他车辆。共十二名受试者被要求仅在第一车道持续驾驶，以便分析来自转动方向盘和控制油门的数据，并在首尔至天安高速公路驾驶条件（SCH）下保持限速100公里/小时。如图1所示，SCH为单向交通，两侧有护栏，由四条车道组成。实验中设有摄像头记录驾驶员面部，以监测其状态及疲劳症状，例如闭眼，如图2所示。选择空旷道路的原因是疲劳驾驶环境通常较为单调；因此，在此环境中不设置障碍物如车辆，以最大化疲劳状态的效率。

3.2. 使用随机森林算法开发NDSCM

根据王M.S之前的研究，发现横向加速度和转向角在检测疲劳状态中具有重要作用。基于此，通过减少输入变量数量以提高计算过程速度，形成了如表2所示的输入变量组合。共有18个输入变量候选用于构建算法。将频率较高的原始数据（100赫兹）处理为平均值、方差、峰值及四阶矩，时间分辨率为1秒。平均值和方差值涉及转向角、横向加速度（Ay）车辆速度（Vel）基于100赫兹原始数据以1秒时间分辨率进行计算。该时间计算包每0.01秒处理一次，意味着每1秒时间段内包含100组数据。因此，可以在高速驾驶行驶距离压力下检测和分析驾驶员状态，以提高驾驶员安全。峰值是指1秒内100赫兹原始数据中的绝对最大值。最大‐最小值是1秒内的最大值和最小值之间的差异。Differ _max值是0.1、0.2和0.5秒间隔的差分值在1秒内的最大值。Delta 3秒值是指3秒内每1秒间隔的差值的绝对值之和。这意味着该算法可检测困倦每分钟车辆采集驾驶数据后3秒的行为。

使用未参与训练RF模型的驾驶员数据来计算算法的性能和错误率。构建算法模型并进行测试共重复 10次。

从表3的结果可以看出，算法的最佳性能出现在使用所有信息的情况下。当使用所有信息（转向角、横向加速度和速度）时，平均、最小和最大错误率分别为0.180、0.158、0.198，这些值低于其他情况。研究发现，速度值影响检测能力。没有速度变量时错误率为0.205和0.226，而使用速度变量后改善为 0.191和0.195。

根据上述研究，使用所有车辆信息来开发算法。为了减少处理时间并提高准确性，输入特征有多种选择，如表4所示。当输入变量中排除平均特征时，错误率为0.181，该结果比应用所有特征的情况更差。使用变化量、Differ _max或delta特征的情况与使用所有特征的情况具有相似的错误率。另一方面，没有最大‐最小值的输入变量组合表现出最佳性能；错误率平均0.168。没有峰值变量的情况还显示出第二名的能力；错误率平均为0.169。特别是最佳情况下的标准差为0.0111，这意味着无论使用何种驾驶员信息，算法的训练都是稳定的。

因此，NDSCM是使用16个输入变量训练的随机森林模型，并结合实时处理系统用于检测困倦行为。该模型的特性见表5。与王之前开发的算法相比，检测准确率低约1.6%。王的结果记录错误率为0.152，而NDSCM显示平均0.168和最小值0.143。然而，输入变量的数量大幅减少（从60减少到16）。此外，先前模型的核心数据集为20秒，而该模型仅需3秒。这些因素影响了处理速度。构建随机森林模型的时间减少了70%以上，生成输入变量的时间加快了80%以上。

表1. 正常与嗜睡状态下的实验安排与流程
Time
下午12:45
下午13:00
13:45
下午2点
下午2点45分

表2。构建正常与嗜睡状态分类模型（NDSCM）的输入变量候选示例
平均
斯特尔
斯特尔
A_s
M_s
D3_s

表3. 使用随机森林的NDSCM相应驾驶信息的总体错误率（N = 10).
转向角度
0.205
最小错误率
最大错误率
标准差

表4. 总体误差或使用随机森林的NDSCM输入组合中被排除特征的比率 N=10)
被排除的特征
错误率
最小错误率
最大错误率
标准差

表5. NDSCM特征总结
使用方法
使用车辆数据
时间分辨率
数据处理时间
必要数据集
输入特征数量
输入特征类型
输出
最小错误率

4. 醉酒与困倦状态分类模型（DDSCM）

4.1. 醉酒状态实验条件

在酒后驾驶实验中，SCH公路分为两部分。该道路包含两种类型：前半部分（30公里）为自由道路，即没有其他车辆；后半部分（33.9公里）为事件道路，设有其他车辆变道和紧急停车点，用于测量反应时间，以进行醉酒状态下紧急情况的影响分析。为了开发DDSCM，使用了来自NDSCM实验中的第一段道路数据（直线驾驶）和困倦数据。紧急停车在驾驶课程开始20 ± 10分钟后伴随响亮的铃声发生。当铃声响起时，驾驶员立即尽快停车。正常状态驾驶在同一道路上于12:45开始，醉酒状态驾驶则于19:00开始。详细信息见表6。在参与者开始醉酒驾驶之前，他们会进含有酒精的晚餐。在此期间，使用如图4所示的设备测量其血液酒精浓度（BAC）。

根据韩国道路交通法第148‐2条，血液酒精含量不低于0.05%但低于0.1%者，将被处以不超过六个月的监禁并处劳役，或处以不超过三百万韩元的罚款。该 0.05% BAC是韩国酒驾处罚的最低标准。因此，参与者在整个实验过程中需保持BAC超过0.05%，并在练习后和正式驾驶前使用BAC测量设备测量BAC。驾驶结束后BAC低于0.05%的参与者驾驶数据被排除，并在一周后进行重新测试。表7显示了驾驶前后测量驾驶员BAC的结果。同时记录驾驶屏幕图像，以分析醉酒状态下的车辆移动，如图5所示。

4.2. 醉酒状态下的紧急停车反应时间分析

关于疲劳状态的模拟车辆实验验证已经完成（王等人，2016）。然而，仍需利用紧急停车反应时间数据来展示针对醉酒情况及酒精对驾驶影响的模拟实验验证。具体而言，对12名参与者在正常状态和醉酒状态下的反应时间分析对于验证模拟器实验及醉酒状态的影响至关重要。分析结果如表8所示。自由度为k−1 ，其中k为被试间变量的数量。对于被试间自由度，变量为自变量，每个变量水平使用不同的受试者组。在本研究中，变量为来自12名驾驶员的反应时间，取决于两种状态：正常和醉酒。

驾驶员反应时间的测量方法如下：即从紧急停车铃响到驾驶员尽快控制制动踏板之间的时间间隔。(1) 从模拟屏幕的录制视频中找出紧急铃声响起以及车辆完全停止的时间。(2) 计算铃响时刻与停止时刻之间的间隔时间。(3) 从总提取驾驶数据中找到速度低于0.1公里/小时的数据。(4) 通过回退过程(2)所得百倍值（因为数据频率为100赫兹）来确定紧急情况首次发生的位置。(5) 计算过程(4)中找到的时刻与制动压力上升时刻之间的差异。

通过这些过程收集到间隔时间，并用于方差分析。在正常驾驶中，反应时间平均值为0.31，标准差为11.14。而在酒后驾驶情况下，平均值和标准差分别为 0.92和40.77。方差分析结果显示，p值和F值分别为 0.005（< 0.05）和12.5，表明酒后驾驶与正常驾驶之间存在显著差异。这意味着与正常状态相比，醉酒驾驶员在紧急情况下的反应能力表现出缓慢且不均匀的特点。该结果表明，当驾驶员平均醉酒程度达到300 %时，包括视觉识别在内的神经过程以及控制踏板和转向等生理过程均变得不稳定。因此，酒后驾驶阶段的驾驶员确实处于醉酒状态，且模拟器实验能够反映驾驶员状态。

4.3. 使用机器学习算法开发DDSCM

用于区分困倦与正常状态的困倦状态分类模型（DNSCM）在4.2节中开发。本部分的目的是开发一种算法以检测并区分困倦和醉酒状态。为了构建该算法模型，使用了自由道路驾驶下困倦状态和醉酒状态的数据。为了获得更高精度，排除了显示模拟驾驶适应时间的前4分钟段以及最后5分钟段。

通过分析图像记录确定了这段排除时间。采集了采集频率高达100赫兹的数据。由于分类困倦和酒后驾驶相对需要较长时间的驾驶数据，因此需要将其简单处理为时间分辨率为3秒的数据集。

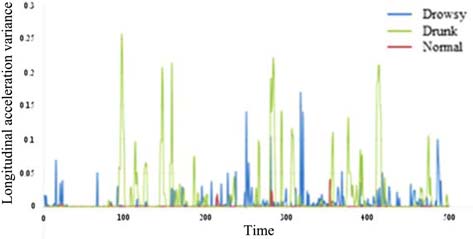
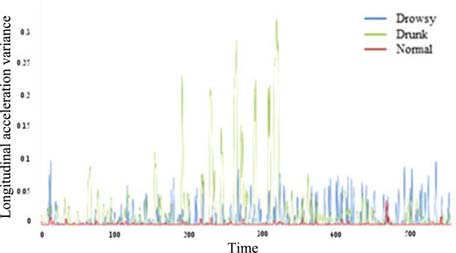
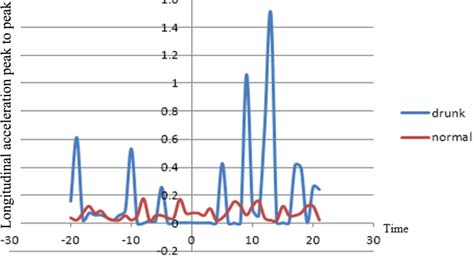
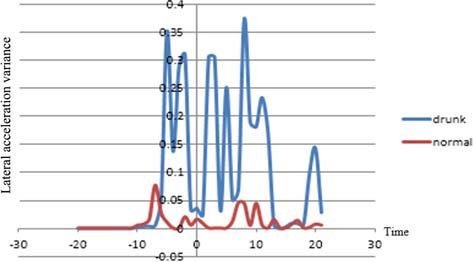
通过分析记录图像，酒后驾驶和疲劳驾驶均表现出类似的横向运动，如蛇形驾驶。纵向值（如方差和峰峰值）的差异如图6至图7所示。正常状态下的纵向加速度方差最低，而醉酒状态的方差最高。这意味着驾驶员在保持恒定速度方面具有最佳控制能力。然而，困倦和醉酒驾驶员失去了保持恒定速度的能力，尤其是醉酒驾驶员，其车辆速度记录的范围更广。

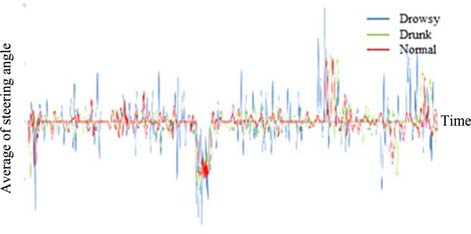
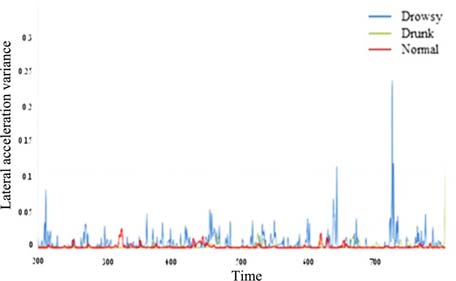
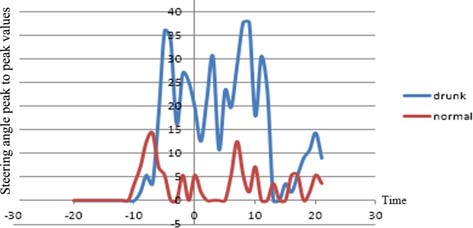
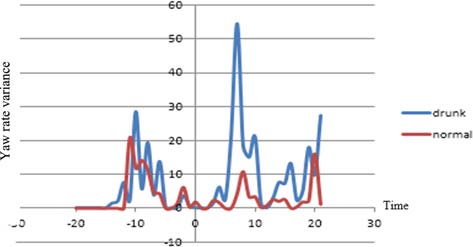
在横向运动方面，疲劳驾驶相比其他状态具有显著的特征，如图8至图9所示。图8是方向盘转角平均值的曲线图。在相同的道路和时刻下，疲劳状态下的数值高于其他状态。此外，疲劳状态的方差具有更高的频率和幅值。然而，没有特定的因素能够区分醉酒和正常状态。这些结果表明，驾驶员在处于疲劳状态时，失去了对方向盘和横向运动的控制能力。通过对图像的分析发现，他们通常会闭眼且无法注视前方。

通过分析确认，困倦状态变量在横向运动中具有明显特征，与其他状态不同。另一方面，酒驾变量在纵向运动方面显示出与其它状态的差异。

基于这些结果，选择加速度方差值来训练机器学习算法。如图6至图9所示，这些图中的峰值点表明有可能构建算法，因此无需使用所有结果数据来训练算法。

表9是输入变量的示例，包含一个60秒时间数据集。Ax_P1 是60秒时间集中纵向加速度的最大方差值，Ax_Pn 是第n个方差值。横向加速度变量的处理方式与纵向加速度相同。总数据集包含3114个输入向量。

表10列出了变量n的结果。训练集占总数的80%，测试集采用自助法，通常为10%。输入数据包采用滑动方法，即无论构建连续系统的时间长度如何，均为前一输入数据之后15秒的数据。决策树的数量为500，隐含神经元数量固定为20，以便比较这两种方法的性能。随机森林的记录结果优于神经网络。随机森林的错误率平均值（10次试验）为14.72%，而神经网络的平均误差率为19.63%。由此结果可知，随机森林在分类困倦和醉酒状态方面具有更好的性能。所有这些表明，随机森林学习算法擅长处理大规模且高复杂性的数据。特别是当算法总共包含7个变量时，其性能最佳。然而，由于相似性导致了这一结果，因此有必要开发具有不同时间集数据和不同n值的算法。

为了确定时间集的影响，通过表11展示了各个时间集在检测困倦和醉酒行为方面的多次试验及结果。使用不同的参数组合得到平均误差率和误差率的标准差。结果显示了参数n与错误率之间的关系，通常它们呈反比，即参数“n”越小，错误率越大。在使用45秒数据生成的错误率中，当参数“n”为15时产生的最低错误率为3.5%，这意味着在45秒数据中没有例外情况，因为所有数据均为3秒时间分辨率。60秒时间数据集也表现出较高的性能，其错误率为4.22%，在所有情况中位列第二。然而，这些组合需要大量的数据以及高性能计算设备来构建和运行算法。因此，为了实现实时分析系统中轻量级系统的快速计算与分析，推荐使用参数“n”为12的45秒数据集以及参数“n”为9的30秒数据集。第一种组合显示错误率为5.5%，第二种组合记录的错误率为7.6%，这些值接近最佳性能（3.5%），且足够可以接受。

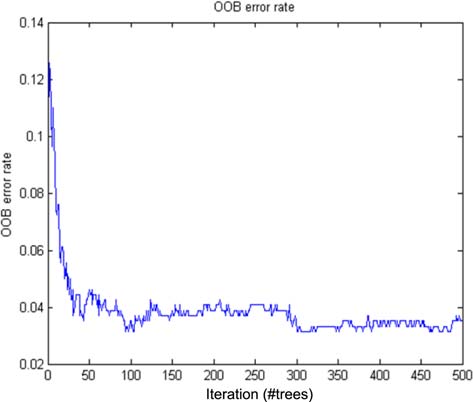
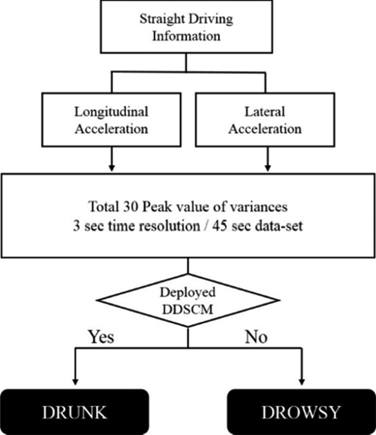
使用45秒数据集和参数获得的错误率在图10中，随机森林模型中的n = 15被绘制为曲线。误差率曲线下降明显，表明其对分类酒驾和疲劳驾驶行为最为有利。表12是DDSCM特征的总结，用于训练和开发该模型。图11展示了使用该模型进行分类酒驾与疲劳状态算法的流程图。

表6. 正常与醉酒状态实验过程。
Time
下午12:45
下午13:00
13:45
下午2点
下午2点45分

表7. 血液酒精浓度。

表8. 紧急停车反应时间分析（正常与酒后）。
阶段T (s)
正常驾驶
醉酒驾驶

表9. 使用60秒数据集训练机器学习算法的输入变量示例。
高阶纵向加速度方差
Ax_P1
0.0951
0.1661

表10. 使用NN和RF对醉驾和疲劳驾驶进行分类的结果，基于固定的60秒数据集。
算法
神经网络
随机森林

表11. 使用随机森林分类醉酒驾驶和疲劳驾驶的总体错误率及对应的时间数据集和n变量。
时间数据集
错平均率
标准偏差

表12. DDSCM特性总结。
使用方法
使用车辆数据
时间分辨率
数据处理时间
必要数据集
输入数量 特征
输入特征类型
输出
最小错误率

5. 面向事件的异常检测模型（AMFOE）

5.1 AMFOE模型开发的实验条件

如5.1节所述，在酒后驾驶实验中，SCH公路上分为两部分：自由道路（30公里）和事件道路（33.9公里）。为了开发 DDSCM，使用了自由道路（直道）的驾驶数据。在本部分中，使用事件道路的驾驶数据来开发 AMFOE。事件道路包含21种变道情况和4种车道受限情况，如表13所示。这些事件被分为三种类型：单次变道、连续两次变道和保持车道。采集的数据频率较高，为100赫兹。由于该高频率，需要将数据基于 100赫兹原始数据每0.01秒进行处理，简化为时间分辨率1秒的数据集。统计方差、平均值和峰峰值（即最小值和最大值之间的差异）等形式被用于此分析，具体取决于所提及的各个事件。

5.2 基于规则方法的AMFOE开发

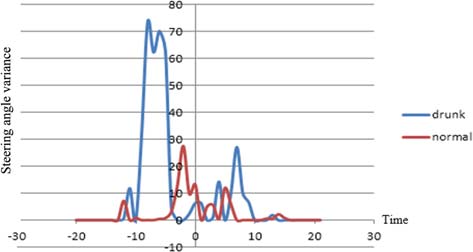
该模型利用车辆变道时的数据，通过基于规则的算法来检测正常状态和异常状态。该算法使用醉酒和正常状态的数据对两种状态（正常和异常）进行分类。假设疲劳驾驶特征与醉酒驾驶特征表现出相似的模式。这一假设基于关于酒后驾驶与疲劳驾驶相似性的研究（道森和里德，1997；威廉姆森和费耶，2000；阿内特等人，2001），以及M个横向变量具有区分疲劳状态的能力（文等，2012）。如图12所示17个原点是车辆通过事件点的时刻，x轴表示时间。具体而言，分析使用了事件点前后2秒的数据。

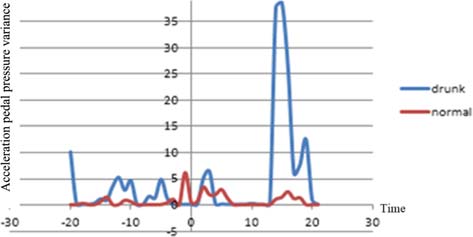
对于车道限制情况，加速踏板压力和纵向加速度的方差及峰峰值具有特定特征，如图12至13所示。驾驶员在酒后驾驶时驾驶车辆不稳定，且醉酒状态下的特征最大值相比正常状态高出300%以上。

在变道一次的情况中，数据显示横向值（如转向角）具有特定特征，如图14至15所示。方差和峰峰值与车道受限事件类似存在差异。另一方面，平均值没有明显的特定模式。这意味着驾驶员在进行单次变道操作时，控制的转向角大致相同，但在准确性和精确性方面有所下降。

两次变道在方差值上表现出一些特征，如图16至17所示。两次变道情况需要驾驶员控制较大的转向角，因此峰峰值不像一次变道那样显示出差异。然而，正如所提到的，当驾驶员处于醉酒状态时，方差值比正常状态更大。

驾驶员在变道情况下有自己控制车辆的习惯，因此本研究所使用的数据分别对每位驾驶员进行分析。为了生成用于构建算法的输入值，本研究使用了正常状态和醉酒状态下最大的3个峰值特征的比值。表14是通过每个事件中醉酒状态值除以正常状态值，并基于最高的3个峰值方差计算得出的比值示例。具体而言，排名#1并不表示特征的最大值，而是表示醉酒状态下最大的方差值除以正常状态下最大的方差值。排名#2的值表示醉酒变道期间第二大的方差除以正常变道期间第二大的方差。

如表14所示，除事件编号21外，所有比值均大于1，这意味着驾驶员处于醉酒状态时的方差高于正常状态。

在本节中，针对每个事件使用了大量的方差数据。例如，在计算事件#1的结果时，仅使用事件#1的正常方差和醉酒状态值。然而，在现实世界中，每种情况都不同，无法像上述那样分组，因此必须建立一个通用的标准方差，以便在所有事件中用于计算方差比。

标准方差反映了驾驶员在变道过程中驾驶员自身特性。从驾驶数据中，可以计算出每次变道情况的3个峰值方差值，如表15所示。在正常状态下，为了调整正常状态下的控制误差，除80到90百分位数外，其余均被排除。排除前10%变量的原因是为了调整噪声带来的误差。然后，标准方差是这些范围内方差的平均值。当变道驾驶数据的方差越来越多时，它会收敛到特定值。具体而言，获取标准方差的流程如下。(1) 获取正常状态下的变道数据 (2) 数据应包含变道交界点前后 ± 2秒 (3) 以3秒分辨率计算方差值 (4) 在各种情况下分别找出并收集3个高峰值 (5) 除去80 到90百分位数以外的峰值 (6) 对剩余的每个峰值计算平均值

例如，在表15中，每个事件有三个峰值方差，数据集为± 2 s，如图12至图17所示。如果使用90百分位数以下的所有数据来计算标准方差，则该值为19.33。此值作为标准过于敏感。然而，80到90百分位数范围内的变量的平均值为49.12，该值适合作为标准使用。在相同的驾驶信息下，针对醉酒和正常状态，使用第一个值进行检测时准确率低于60%，特别是由于其高敏感性，对正常状态数据的误检率超过一半。另一方面，当使用49.12作为检测基准时，准确率超过80%。这意味着80到90百分位数范围适用于计算标准方差。因此，在特定状态（待估计状态）累积的10个事件的方差中，排除最高和最低各20%的数据，以调整因计算标准方差范围带来的检测误差。经过此过程后剩余的变量即为目标方差。表16是基于标准方差计算的比值，除事件20外，所有结果均大于1。

由于需要附加设备（如摄像头）将车道受限情况与自由驾驶区分开来，导致数据获取困难，因此本算法未使用对车道受限情况的分析。

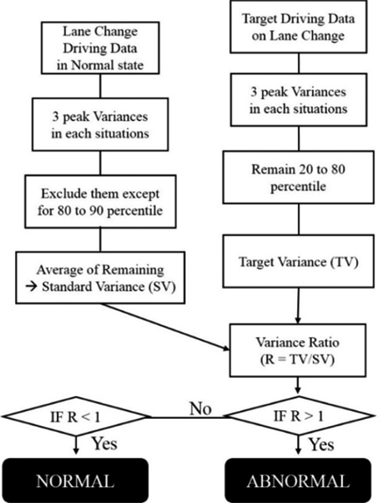
基于上述分析，开发了包含多个检测异常状态步骤的AMFOE模型，如图18所示。第一步是收集驾驶数据、横向加速度和转向角，在驾驶员处于正常状态并尝试变道时，如图12至图17所示。然后，从这些数据中计算出每个事件的多个三个峰值方差，如表15所示。接着，将80到90百分位数的平均值收敛到一个特定值，称为上述的标准方差。第三，收集目标驾驶数据中三个峰值转向角与横向加速度方差的方差比，并剔除最高和最低的20%数值。如果结果值大于1，则认为该驾驶员为异常。

该算法有一些可用的特征。特征组合有多种选择，例如使用全部6个特征，或仅使用等级1和2值的4个特征。几种选项的结果汇总于表17。结果显示，仅使用车辆信息即可实现对异常状态的高准确率检测。当算法仅使用2个特征（转向角等级#1和横向加速度等级#1）时，准确率达到最高。然而，由于交通和振动等其他噪声因素，在实际驾驶情况下建议使用6个特征或4个特征。此外，该算法是通过变道来检测异常状态的。为了获得更高的准确率，建议通过多个事件的总检测结果来使用此算法。例如，如果异常状态的标准是在最近10次变道操作中该算法检测到异常超过7次，则在这些实验结果中准确率高于95%。

表13. 将每个事件分类为三种情况
Type
1车道变换
2车道变换
无变化 （限车道）

表14. 使用所有驾驶员数据，基于各事件的三个峰值方差计算的方差比平均值。
转向角
#1
2.97
8.96
256.0
…

表15. 驾驶员‘A’在正常状态变道情况下各事件的一次变道3个峰值转向角方差示例及标准方差的计算。
一次变道事件的3个峰值方差
Peak
#1
#2
#3

表16. 使用驾驶员‘A’的标准方差，基于各事件的三个高峰值方差值得到的方差比示例。
转向角
#1
2.51
3.17
15.98
…

表17. 按输入特征数量和每个事件的阈值数量划分的多种组合选项的结果
数量
6个特征
4个特征
2个功能

表18. AMFOE 特性总结。
使用方法
使用车辆数据
时间分辨率
数据处理时间
必要数据集
输入特征数量
输入特征类型
输出
最小错误率

6. 三状态检测系统的建议

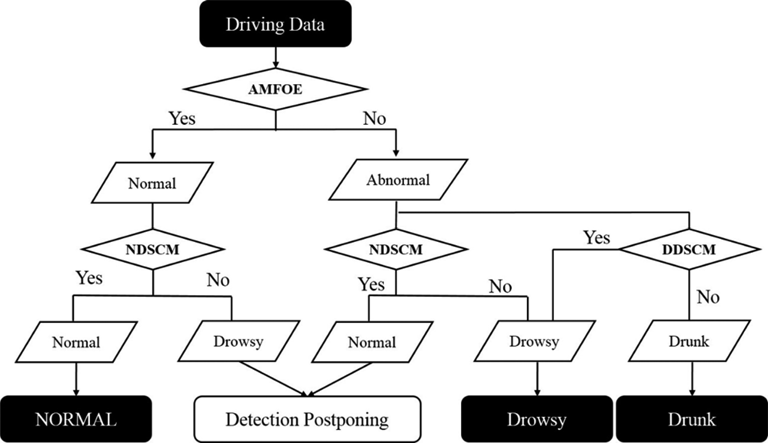
基于三种算法模型的开发；NDSCM、DDSCM和AMFOE，本部分提出了用于检测3种状态的系统，如图19所示。

首先，对AMFOE进行驾驶数据处理。该模型为基于规则的算法，使用转向角和横向加速度。该算法将状态分为两类：正常和异常。在第一步中使用 AMFOE的原因是，该基于规则的模型操作简单。此外，先在大框架下对状态进行分类更为合理。如果状态被判定为正常状态，则启动NDSCM进行检测。NDSCM使用转向角、横向加速度和车辆速度，利用这些数据检测疲劳状态。如果该模型判断为正常状态，则系统得出驾驶员处于正常状态的结论。然而，如果该模型判断为疲劳状态，则决策将推迟到下一组数据，因为所有模型均可连续运行。具体而言，系统可通过重复操作直至得出准确决策。如果AMFOE判定驾驶员处于异常状态，则启动两个模型进行操作。第一个是NDSCM，该模型用于对驾驶员状态进行分类。若判断为正常状态，则系统按照上述正常‐疲劳判断方式进行处理。DDSCM也具有对驾驶员状态进行分类的作用。DDSCM是利用横向和纵向加速度来检测并分类疲劳状态和醉酒状态的模型。如果该模型显示为醉酒状态，则判定驾驶员处于醉酒状态。疲劳状态需由NDSCM和DDSCM同时判断确定。

该系统是一个利用3个简单模型实现精密检测的示例。仅使用一个模型难以精确检测醉酒、困倦和正常等状态。然而，若结合多个简单的算法模型，则可以实现。这意味着可检测更多状态，例如低血压药物也使用类似该系统的简单模型组合进行分类。

7. 结论

本研究提出了三种用于分类正常、困倦和醉酒驾驶的算法模型。

为了构建三个模型，进行了两种类型的实验；第一种是自由道路驾驶，以获取关于困倦状态和正常状态的驾驶信息；第二种是事件道路驾驶，以获取酒后驾驶信息和正常驾驶信息。事件课程道路包含两个部分；前半段道路类似于困倦状态实验中的自由道路，而后半段则有许多障碍物，如其他车辆和紧急停车点。通过模拟器采集了加速度、转向角、横摆率、速度等实时驾驶数据。共有12名参与者完成了实验，且他们都具备参与这些实验的资格。

利用这些驾驶数据，开发了首个用于区分困倦行为与正常行为的模型。该模型称为正常与疲劳状态分类模型（NDSCM），是在王的研究基础上改进而来的。该随机森林模型采用来自转向角、横向加速度和车速的16个输入变量，时间分辨率为1秒，数据集时长为3秒。其错误率平均为0.168，最小值为0.143，最小值低于王的错误率（0.152）。此外，构建和运行该随机森林模型所需时间减少了70%以上，且准确率相近或更优。

第二个模型称为醉酒与困倦状态分类模型（DDSCM），该模型基于自由道路数据的特征。在分析和开发之前，收集紧急停车反应时间以分析酒精对驾驶情况的影响，并验证这些模拟器实验。结果表明，p值低于0.05，酒精影响驾驶员的反应能力，这些实验已得到验证。在此算法模型中，由于数据的复杂性和大规模数据，采用了机器学习方法。该模型包含多个参数。随机森林算法和人工神经网络的输入变量是纵向和横向加速度方差值，这些值可作为区分驾驶员状态的特征。N表示数据集中峰值方差值的数量。使用60秒数据集发现，当导入不同的N值时，随机森林（RF）在对醉酒状态和困倦状态进行分组方面的性能高于人工神经网络（ANN）。然后结果表明，当N值和时间数据集较小时，错误率会变大。因此，最佳检测点是使用45秒数据集和N = 15。使用这些参数的错误率小于5%。

最后一种算法AMFOE利用基于事件道路驾驶数据的机器学习方法，通过变道驾驶数据检测异常状态。侧向运动变量的方差和峰峰值，例如加速度或转向角是变道情况下的显著因素。另一方面，在车道受限情况下，纵向因素表现出差异。基于这些结果，标准方差（SV）通过正常状态下的变道中第80百分位到第90百分位方差的平均值计算，以调整误差。目标驾驶（TV）的方差（即在变道中需要检测的状态）同样排除上下20%的数据，以调整计算标准方差时产生的误差。当方差比（TV/SV）的值大于1时，算法判定为异常状态。当特征数量为4且阈值为2时，每次变道的准确率均超过92.3%。

在本研究中，如前所述，已开发出用于检测3种状态的模型。然而，在以下几个方面仍存在一些局限性。例如，AMFOE仅在积累了足够数据后才能运行，且该方法需要在真实环境中进行验证。此外，所有模型目前仅用于分类2种状态。尽管如此，它们展示了仅通过易于获取的驾驶数据组合即可对驾驶员状态进行分类的可能性。图19展示了使用三种所开发的模型来检测3种状态的系统示例。未来，通过在复杂条件下以及针对不同类型驾驶员开展实验，可能会进一步提升这些模型的性能。