【初中数学 课本阅读】七年级上册 第一章 有理数

第一章 有理数

1.1 正数和负数

负数运算？ 3-（-3）？？？
在正数前加上符号“-”（负）的数叫负数
在正数前面也加上符号“+”（正）表示正数
一个数前面的“+”，“-”叫做数的符号
0既不是正数，也不是负数

• 正负数：表示是一种相对关系，如前后，左右，上下，0表示这对关系的分界线

1.2 有理数

小学学过的数：正整数、0、负整数
正整数、0、负整数统称为整数
正分数、负分数统称为分数
整数和分数统称为有理数
数轴

• 在数学中，可以用一条直线上的点表示数。这条直线叫做数轴。
• 满足要求：
  • 在直线上任取一个点表示数0，这个点叫做原点
  • 通常规定直线上从原点向右或上为正方向，从原点向左或下为负方向
  • 选取适当的长度为单位长度，直线上从原点向右，每隔一个单位长度取一个点，依次表示1,2，3···；从原点向左，用类似方法依次表示-1，-2，-3···。

1.2.1 相反数

符号不同的两个数互为相反数
一般地，a和-a互为相反数。特别地，0的相反数是0
在任意一个数前面添加上负号，新的数就表示原数的相反数

1.2.2 绝对值

一般地，数轴上表示数a的点与原点的距离叫做数a的绝对值。
显然，0的绝对值是0

• 一个正数的绝对值是它本身
• 一个负数的绝对值是它的相反数
• 0的绝对值是0
  有理数的大小判定： 数学中规定：在数轴上表示有理数，它们从左到右的顺序，就是从小到大的顺序，即右边的数大于左边的数

1.3 有理数的加减法

引入负数的加减法

• 符号相同的两个数相加减，结果的符号不变，绝对值相加
• 符号相反的两个数相加减，结果的符号与绝对值较大的数的符号保持一致，并用较大的绝对值减去较小的绝对值
  有理数加减法运算规律：
• 满足交换律：两个数相加减，交换两个数的位置，和不变
• 满足结合律：三个数相加减，可以改变计算顺序

有理数减法法则：

• 减去一个数，等于加上这个数的相反数

1.4 有理数的乘除法

我们已经熟悉正数和0的乘除法运算，引入负数后。乘除法运算如何进行呢？
有理数乘法法则：
一般地，两数相乘，同号得正，异号得负，绝对值相乘

• 任何数与0相乘，都得0
• 相反数：自身×-1
• 倒数：两个数相乘的积为1
• 满足交换律、结合律、分配律

有理数的除法法则：
除法是乘法的逆运算：除以一个不等于0的数，等于乘这个数的倒数
一般地，两数相除，同号得正，异号得负，并把绝对值相除

• 0除以任何一个不等于0的数，都得0

1.5 有理数的乘方

一般地，n个相同因数的积的运算，叫做乘方，乘方的结果叫做幂。记作$a^n$，a叫做底数，n叫做指数

• 负数的奇次幂是负数，负数的偶次幂是正数
• 正数的任何次幂都是正数
• 0的任何正整数次幂都是0

做有理数的混合运算时，应注意以下运算顺序：
１．先乘方，再乘除，最后加减；
２．同级运算，从左到右进行；
３．如有括号，先做括号内的运算，按小括号、中括号、大括号依次进行．

1.6 科学计数法与近似数

**科学计数法：**把一个大于10的数表示成a×$10^n$的形式

• a大于或等于1且小于10，n是正整数
• 与实际数有一定差别的数，就是近似数

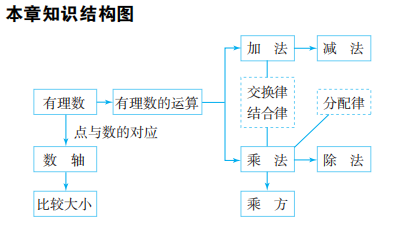
小结