XGBoost原理及公式推导(参考官网文档)

本文主要是参考XGBoost官方网页的学习笔记。
参考网页：https://xgboost.readthedocs.io/en/latest/tutorials/model.html

Introduction to Boosted Trees

XGBoost是“Extreme Gradient Boosting”的简称，“Gradient Boosting”这一术语是在“Greedy Function Approximation: A Gradient Boosting Machine, by Friedman. ”论文中提出的。XGBoost就是基于该原始模型的。如下链接是一个关于梯度提升树的教程，本文大部分内容都是基于xgboost作者的链接ppt文档https://homes.cs.washington.edu/~tqchen/pdf/BoostedTree.pdf。GBM(提升树)已经存在有一段时间了，关于这个话题的材料有很多，本教程通过监督学习解释提升树。

Elements of Supervised Learning

对于监督学习，给定训练集(包含多维特征$x_i$)和要预测的目标变量$y_i$。

Model and Parameters

监督学习模型预测是对于给定的$x_i$预测$y_i$。以常见的线性模型为例，预测值是特征的线性组合${\hat{y}}_i=\sum _j{\theta }_j{x}_{ij}$。根据任务是回归还是分类，预测值可以有不同的解释。例如，在逻辑回归里，可以用logisitic函数将线性组合结果转化成属于正类的概率；在排序问题里，可以将线性组合结果看作是排序分数。参数是不确定，需要从数据中学习。在线性回归里，参数是指系数$\theta$。

Objective Function: Training Loss + Regularization

基于对$y_i$的不同理解，可以有不同问题，如回归、分类、排序，等等。对于给定的训练集，我们应该找一种求最优参数的方法，如定义目标函数，度量给定的一组参数在模型上的表现。目标函数通常包含两部分：训练集损失和正则化项。
$$obj(\theta )=L(\theta )+\Omega (\theta )$$
其中，$L(\theta )$是训练集损失，度量模型在训练数据上的准确性，$\Omega$是正则化项。如，MSE训练损失
$$L(\theta )=\sum _i(y_i-{\hat{y}}_i{)}^2$$
逻辑回归里的Logistic损失
$$L(\theta )=\sum _i[y_{i}ln(1+e^{-{\hat{y}}_i})+(1-y_i)ln(1+e^{{\hat{y}}_i})]$$
正则化项控制模型的复杂度，避免过拟合。为了形象解释，请看下图描述的的问题：用一个分段函数拟合图片左上角给定的输入点。你认为下面三种哪个拟合得最好？

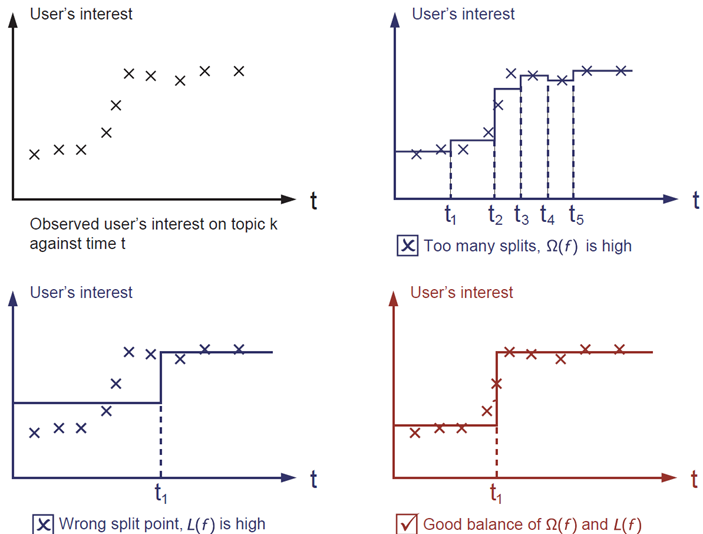
最好的是红色的那个。因为我们想要的模型是既简单又具有预测性的，二者之间的均衡在机器学习里又称为“偏差-方差均衡”(bias-variance tradeoff)。

Why introduce the general principle?

上述介绍的内容是监督学习的基本要素，它们自然地组成了机器学习工具箱的各个模块。描述提升树和随机森林的异同，通过公式理解算法，有助于理解模型学习过程，及剪枝和平滑等启发式方法。

Tree Ensemble

首先，我们学习下Xgboost集成树。树集成模型即是一组分类和回归树(CART)。下面看一个分类树，具体场景是判断一群人是否喜欢电脑游戏。

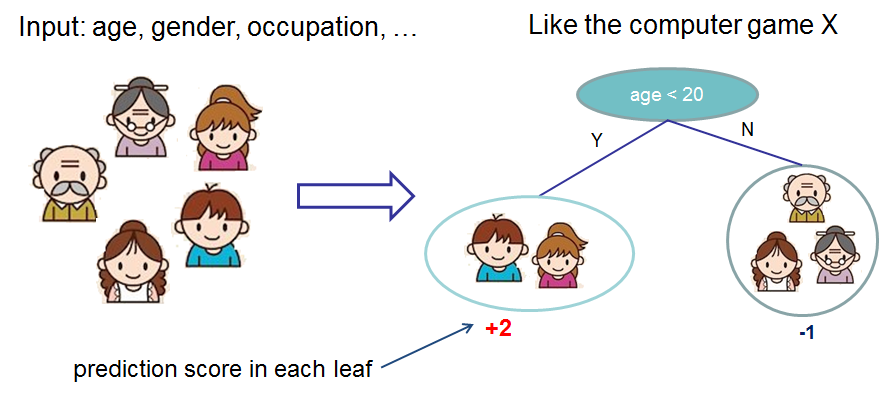
将每个人划分到不同的叶子，并根据每个人所在的叶子给该人分配分数。CART不同于决策树，决策树的叶子只包含决策值，CART里的一个得分与每一个叶子都有关联，这给了我们更丰富的解释，超出了分类，这也使得统一的优化步骤更简单。通常，单棵树在实践中的表现不够强，实际会用的是集成树模型，即将多棵树的预测求和。

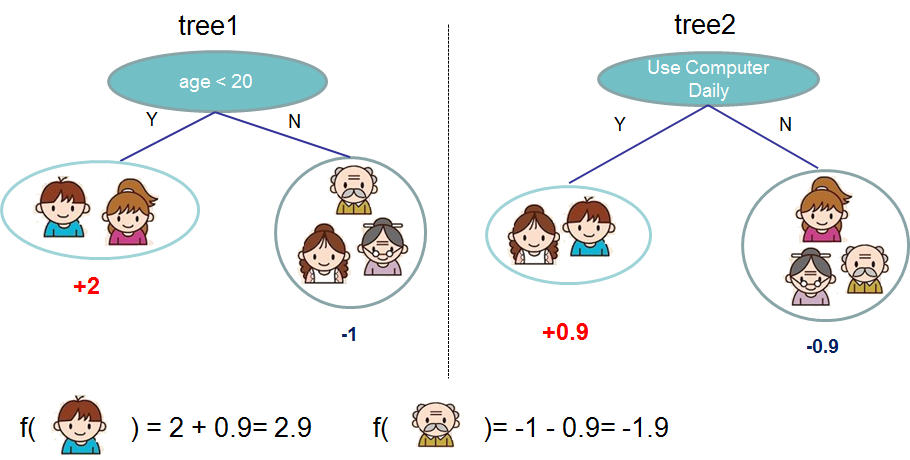
上图就是两棵树集成的一个例子，最终每个人的预测分数是由该人在每棵树获得的得分求和。需要注意的是，该例中两棵树都是单独构建的，用数学公示表示该公式如下
$${\hat{y}}_i=\sum _{k=1}^K{f}_k(x_i),f_k\in \mathcal{F}$$
这里，是树的棵树，是函数空间里的函数，是所有可能的CARTS的集合。因此，要优化的目标可记做
$$\text{obj}(\theta )=\sum _i^{n}l(y_i,{\hat{y}}_i)+\sum _{k=1}^K\Omega (f_k)$$
随机森林和提升树的主要不同在于模型训练过程。

Tree Boosting

树怎么学习？和所有监督学习一样：定义一个目标函数，然后优化它。假如有如下目标函数
$$\text{obj}=\sum _{i=1}^{n}l(y_i,{\hat{y}}_i^{(t)})+\sum _{i=1}^t\Omega (f_i)$$

Additive Training

首先，我们想问“树的参数是什么”？我们需要学习的是函数$f_i$，包含树的结构和叶子的分数。这比传统的利用梯度法求解的优化问题要难得多。由于同时训练所有的树不容易，我们选用另一策略：将已经学习的树固定，每次向其中添加一棵新的树。在第$t$步获得的预测值记为${\hat{y}}_i^{(t)}$，则
$$\begin{gathered} {\hat{y}}_i^{(0)}=0 \\ {\hat{y}}_i^{(1)}=f_1(x_i)={\hat{y}}_i^{(0)}+f_1(x_i) \\ {\hat{y}}_i^{(2)}=f_1(x_i)+f_2(x_i)={\hat{y}}_i^{(1)}+f_2(x_i) \\ \dots \\ {\hat{y}}_i^{(t)}=\sum _{k=1}^t{f}_k(x_i)={\hat{y}}_i^{(t-1)}+f_t(x_i) \end{gathered}$$
接下来要问，每一步我们想要的哪一棵树？一个很自然的想法是增加的那一棵树可以优化目标函数
$$\begin{gathered} {\text{obj}}^{(t)}=\sum _{i=1}^{n}l(y_i,{\hat{y}}_i^{(t)})+\sum _{i=1}^t\Omega (f_i) \\ =\sum _{i=1}^{n}l(y_i,{\hat{y}}_i^{(t-1)}+f_t(x_i))+\Omega (f_t)+constant \end{gathered}$$
其中$\Omega (f_i)$是正则化项。如果用MSE作为损失函数，目标函数变成如下形式
$$\begin{gathered} {\text{obj}}^{(t)}=\sum _{i=1}^n(y_i-({\hat{y}}_i^{(t-1)}+f_t(x_i)){)}^2+\sum _{i=1}^t\Omega (f_i) \\ =\sum _{i=1}^n[2({\hat{y}}_i^{(t-1)}-y_i)f_t(x_i)+f_t(x_i{)}^2]+\Omega (f_t)+constant \end{gathered}$$
MSE损失函数包含一阶残差项和一个平方项，相比之下，其他的损失函数(如logistic损失)就不会得到这么漂亮的形式。所以，通常将损失函数在$x_i$进行二阶泰勒展开
$${\text{obj}}^{(t)}=\sum _{i=1}^n[l(y_i,{\hat{y}}_i^{(t-1)})+g_i{f}_t(x_i)+\frac{1}{2}{h}_i{f}_t^2(x_i)]+\Omega (f_t)+constant$$
其中
$$\begin{gathered} g_i={\partial }_{{\hat{y}}_i^{(t-1)}}l(y_i,{\hat{y}}_i^{(t-1)}) \\ {h}_i={\partial }_{{\hat{y}}_i^{(t-1)}}^{2}l(y_i,{\hat{y}}_i^{(t-1)}) \end{gathered}$$
将所有的constant项去掉，在第t步的目标函数变为
$$\sum _{i=1}^n[g_i{f}_t(x_i)+\frac{1}{2}{h}_i{f}_t^2(x_i)]+\Omega (f_t)$$
该函数就是我们构建新树的优化目标，该函数有个很大的优势，即只依赖$g_i$和$h_i$。这就是Xgboost可以支持“自定义损失函数”的原因。将$g_i$和$h_i$作为输入，即可用相同的求解器优化每一个损失函数，包括logistic regression和加权logistic regression。

Model Complexity

下面考虑树的复杂度$\Omega (f)$。首先，重新定义树$f(x)$为
f t ( x ) = w q ( x ) , w ∈ R T , q : R d → { 1 , 2 , ⋯   , T } . f_t(x) = w_{q(x)}, w \in R^T, q:R^d\rightarrow \{1,2,\cdots,T\} . ft​(x)=wq(x)​,w∈RT,q:Rd→{1,2,⋯,T}.
这里，$w$是叶节点上的得分向量，$q$是将每个样本分配到相应叶子的函数，$T$是叶子数。
在XGBoost里，如下定义复杂度
$$\Omega (f)=\gamma T+\frac{1}{2}\lambda \sum _{j=1}^T{w}_j^2$$
当然，不止一种方式可以定义复杂度，但实践中上面提到的就能很好得起作用。正则化项在很多树模型包里都没有很好地处理，甚至直接忽略。这是因为，传统树模型只强调提升模型的纯度，而模型复杂度控制采用启发式方法。通过公式定义，我们可以更好得理解学习器训练过程，并起获得较好的实践结果。

The Structure Score

下面是公式推导里神奇的部分！将树模型重新公式化表示之后，可以将第棵树的目标值记作：
$$\begin{gathered} {\text{obj}}^{(t)}\approx \sum _{i=1}^n[g_i{w}_{q(x_i)}+\frac{1}{2}{h}_i{w}_{q(x_i)}^2]+\gamma T+\frac{1}{2}\lambda \sum _{j=1}^T{w}_j^2 \\ =\sum _{j=1}^T[(\sum _{i\in I_j}{g}_i)w_j+\frac{1}{2}(\sum _{i\in I_j}{h}_i+\lambda )w_j^2]+\gamma T \end{gathered}$$
这里 I j = { i ∣ q ( x i ) = j } I_j = \{i|q(x_i)=j\} Ij​={i∣q(xi​)=j} 是被分配到第 $j$ 个叶子节点的人的下标集。注意，在上述公式第二行，由于所有在相同叶子上的人获得的分数一样，所以可对求和公式的下标重新表示。利用 $G_j={\sum }_{i\in I_j}{g}_i$ 和 $H_j={\sum }_{i\in I_j}{h}_i$，可进一步简化公式：
$${\text{obj}}^{(t)}=\sum _{j=1}^T[G_j{w}_j+\frac{1}{2}(H_j+\lambda )w_j^2]+\gamma T$$
在上式中，$w_j(j=1,2,\cdots ,T)$ 之间是彼此独立的，公式 $G_j{w}_j+\frac{1}{2}(H_j+\lambda )w_j^2$是二次的。对于给定的树结构$q(x)$，可求使目标最优的$w_j$及相应的最优目标函数值：
$$\begin{gathered} w_j^{\ast }=-\frac{G_j}{H_j+\lambda } \\ {\text{obj}}^{\ast }=-\frac{1}{2}\sum _{j=1}^T\frac{G_j^2}{H_j+\lambda }+\gamma T \end{gathered}$$
上述最后一个式子度量了树结构$q(x)$的好坏。

如上述公式听起来复杂，可以参考图片理解得分是怎么计算的。对于给定的树结构，在每个叶子节点上推算统计量$g_i$和$h_i$，并求和，利用公式$obj$计算出树的好坏程度。“得分”看起来像决策树里的“不纯度”，此外，其计算也考虑了“模型的复杂度”。

Learn the tree structure

现在，我们有一种方式去度量一棵树的好坏，理想情况下，我们可以遍历计算每一棵树后选取最好的一个，但实际上这是棘手的。通常，我们会试着每次优化树的一层。集体地说，试着将一个叶节点分裂成两个叶节点，分数增益是
$$Gain=\frac{1}{2}\left[\frac{G_L^2}{H_L+\lambda }+\frac{G_R^2}{H_R+\lambda }-\frac{(G_L+G_R{)}^2}{H_L+H_R+\lambda }\right]-\gamma$$
上述公式可以分解成(1)在新左叶节点上的分数 (2)在新右叶节点上的分数 (3)在原来叶节点上的分数 (4)新增的叶节点引入的正则化项。一个重要的事实：如果增益小于$\gamma$，加入分支会表现更好，这即是树模型里的剪枝技巧。
对于真实的数据，通常我们想寻找一个最优切分点。为了高效得完成这个工作，首先将所有样本排序，如下图

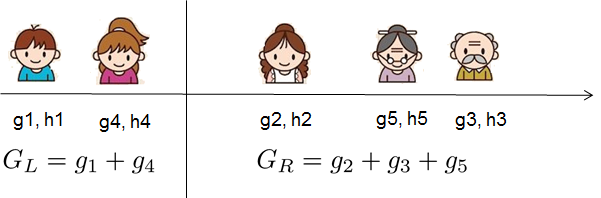
从左到右遍历即可找出所有可能的切分结构及相应的得分。