关于格雷码的一点思考

关于格雷码的一点思考(图片修复)

什么是格雷码

在一组数的编码中，若任意两个相邻的代码只有一位二进制数不同，则称这种编码为格雷码（Gray Code），另外由于最大数与最小数之间也仅一位数不同，即“首尾相连”，因此又称循环码或反射码。由于这种特点，就可以避免二进制编码计数组合电路中出现的亚稳态。格雷码常用于通信，FIFO 或者 RAM 地址寻址计数器中。

格雷码属于可靠性编码，是一种错误最小化的编码方式，因为虽然二进制码可以直接由数/模转换器转换成模拟信号，但在某些情况，例如从十进制的 7 转换为 8 时二进制码的每一位都要变，能使数字电路产生很大的尖峰电流脉冲。而格雷码则没有这一缺点，它在相邻数字间转换时，只有一位产生变化。它大大地减少了由一个状态到下一个状态时逻辑的混淆。

从广义上讲，格雷码（Gray Code）不止一种，在没做特殊说明的情况下，格雷码是指经典格雷码。下面是深度为4的二进制码和格雷码的对照表。

二进制码	格雷码	二进制码	格雷码
0000	0000	1000	1100
0001	0001	1001	1101
0010	0011	1010	1111
0011	0010	1011	1110
0100	0110	1100	1010
0101	0111	1101	1011
0110	0101	1110	1001
0111	0100	1111	1000

​ ​

二进制码与格雷码的转换及其推理过程

我们先将一个四位的二进制码的四个位分别设为A、B、C、D。

我们先从格雷码的最低位等于0的情况开始列写逻辑函数

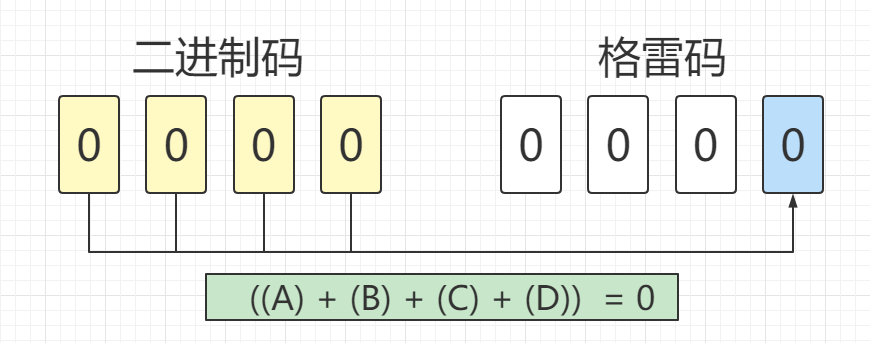
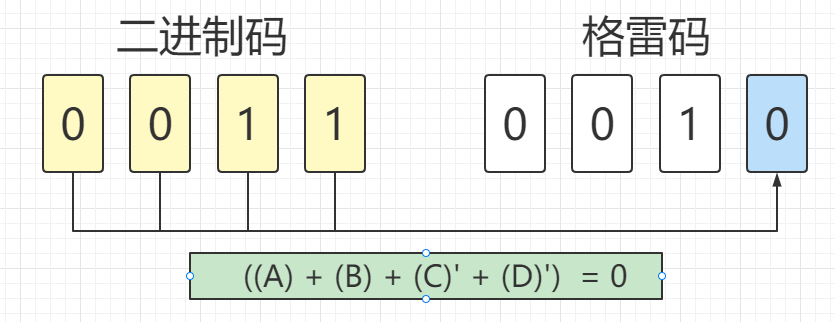
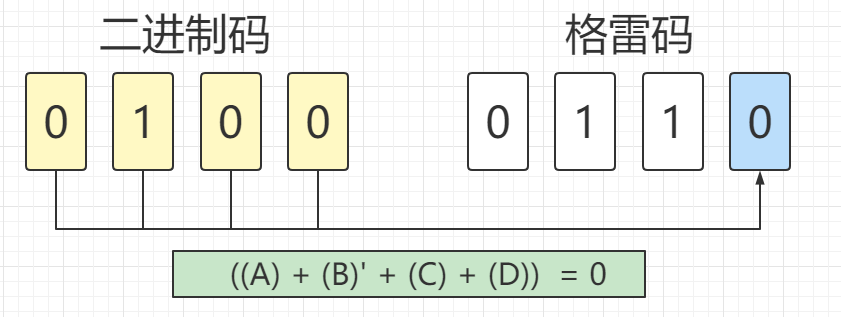
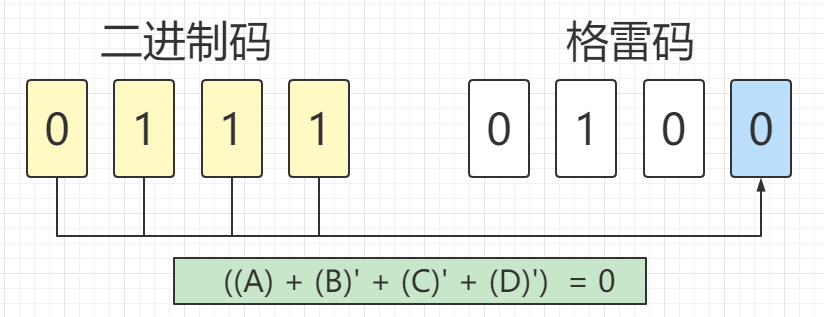
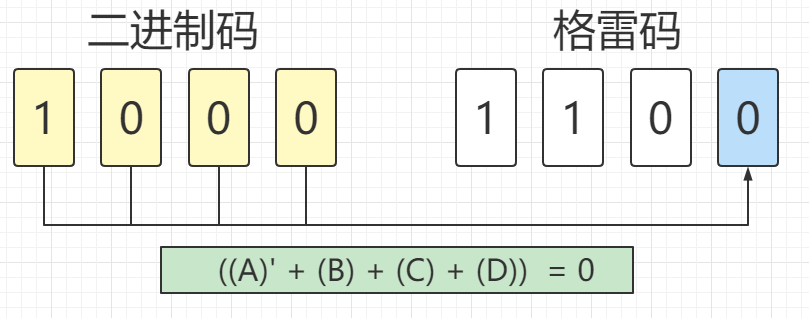
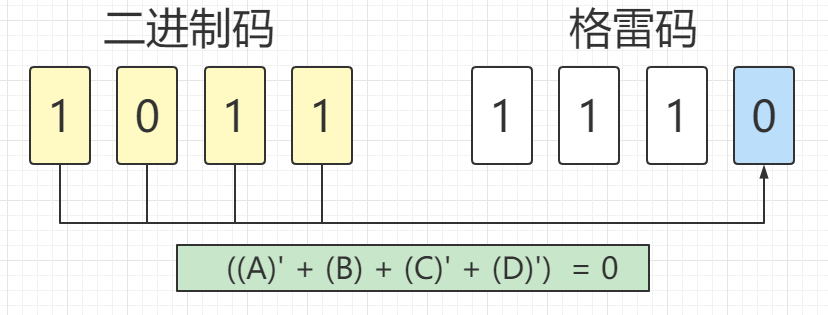
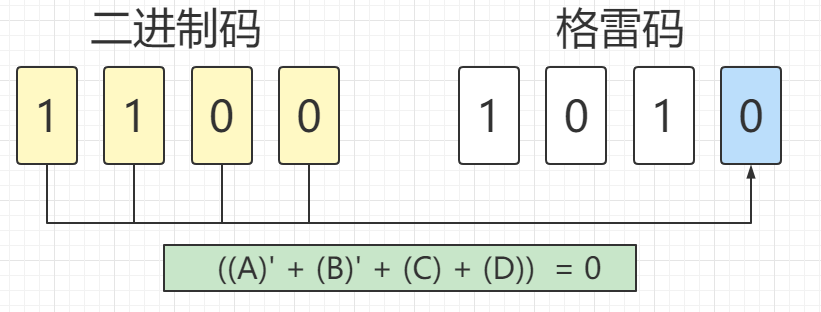
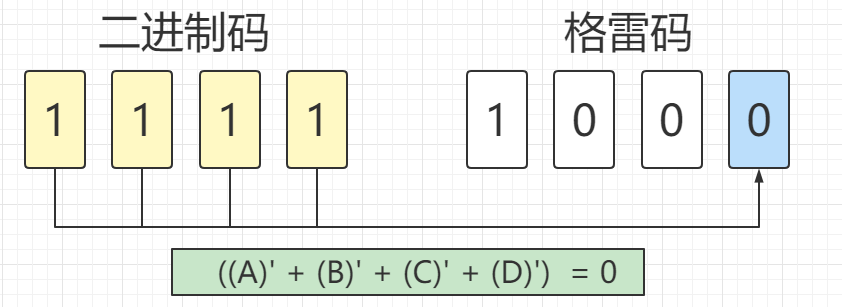
通过比较第1、3、5、7张图片上的公式可以看出，A和B对于公式结果没有影响，所以可以省去。

这时候再结合 格雷码的最低位等于1的情况（用C、D位列写逻辑函数来表示，形式上类似于**（© * (D)')**），由于篇幅原因这里就不一一写出。

我们将格雷码的最低位设为F，那么通过C、D位的公式可以推导出：
$$((C{)}^{\prime }+(D{)}^{\prime })\ast ((C)+(D))=F$$
或
$$((C{)}^{\prime }\ast (D))+((C)\ast (D{)}^{\prime })=F$$
由上面两个式子可以得出
$$C^{\prime }D+C{D}^{\prime }=F$$
即
$$C⨁D=F$$

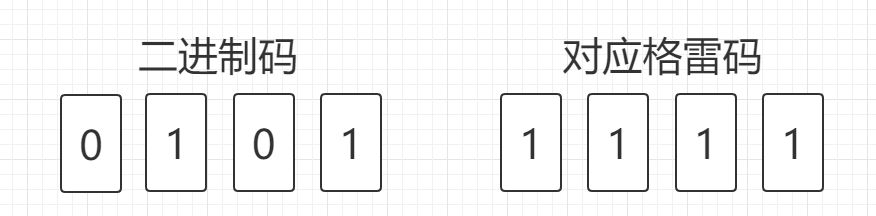
同理，可以得到二进制码转格雷码的方法：从最右侧开始，依次向左，将一位与其左边一位相异或，得到的数放入该位对应位置。

转码方式的核心思想

我们知道了转码方式，那为什么这样转码就可以产生相邻位转换仅变化一位的效果呢？

我们将6、7、8 三个的二进制数转化成波形图

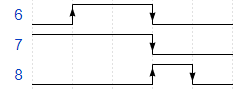
可以观察到，“6”有两处“电平变换”，“7”有一处，“8”有两处。对比6和7，变换数量发生了变化，对比“6”和“8”，变换的位置发生了变化。再对比更多的二进制数，可以发现，每一个二进制数的“电平变换”的分布是独有的，而且这种分布在相邻的数之间仅差一位。（这仅仅是我观察得到的结论，还没有严谨的证明，有证明或证伪方法的朋友可以提出来）这用我们就可以用上面异或的方式来表示“电平变换”的分布，就可以得到格雷码

其他转码方式

经典格雷码编码的核心思想就是通过某种运算来表示“电平变换”的分布，那还有什么方式可以产生同样的效果呢？

同或转换

就是将经典格雷码转码方式中的异或运算改为同或，这样可以得到经典格雷码的反码。

右侧异或

最右侧的最低位不变，从第二位开始，依次向左，位与右侧一位进行异或操作。当然，这样有一个问题，就是一个四位的二进制码很可能需要五位才可以表示，可能因此这种方法并不常用

解码

知道了编码，解码也就非常简单了，只需要进行逆向运算就可以，我们以经典格雷码为例：

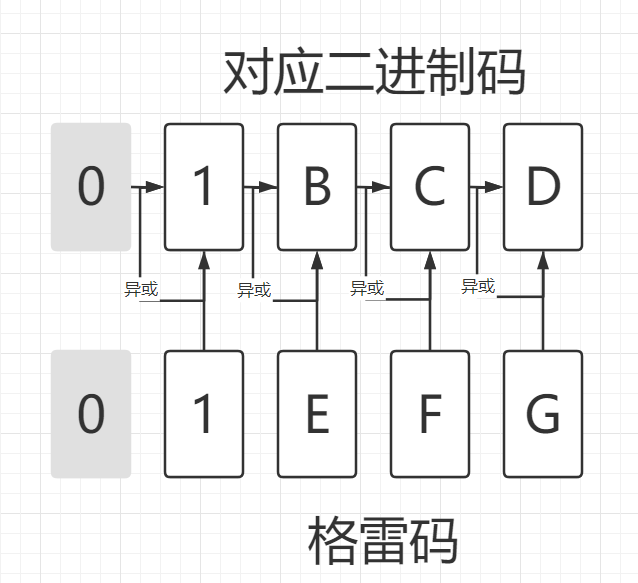
首先我们要找到格雷码的最高位，假设最高位是第四位

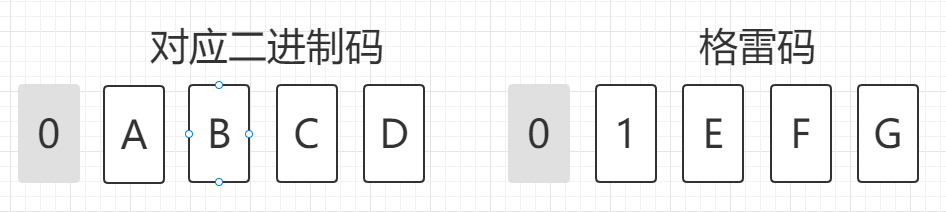
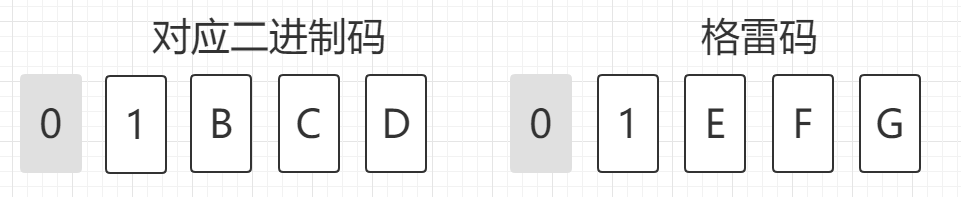
最高位是第四位所隐含的条件是格雷码和二进制码的第五位都是0，所以
$$A⨁0=1$$
易得 $A=1$

在来看下一位“E”

$$ &1\bigoplus B&=E \\ （由异或的性质可得） \implies & 1\bigoplus E&=B $$

需要注意的是这里格雷码的“E”是已知量，所以我们可以求得“B”，再通过“B”和“F”求得“C”，以此类推。

其他解码方式就不做介绍了，大家可以自己试着推导一下，相信你们也会有所收获