物理上定义力矩是力对物体产生转动作用的物理量,这里我们想象一下现实中的力矩现象,比如陀螺,老式摇动柴油发动机,打隧道用的隧道机械都有力矩在其中。
这里我们看一下老式柴油发动机的摇把,如下图:
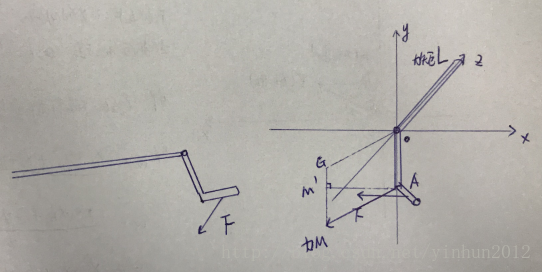
手对摇把产生OA的半径圆的切线方面力F摇动,那么会产生一种沿着Z轴的力矩L,物理上把求力矩L定义为力F 乘 力臂OA,既:L = F*OA。
这里力矩L可以看作一个和Z轴重合的向量,力矩L的数量值等于力F作用的那一刻(那一瞬间,后面我们在微分中会讲解一瞬的意义)与力臂OA组成的平行四边形(特殊情况下比如F为切线就是矩形)的面积,上图中力M就是普通情况,求AM'和MG的乘积救得到力矩的向量的模长。
扯了这么多,其实就是阐述力矩的这种定义,数学上我们把计算力矩称为计算叉积,接下来我们继续观察叉积的几何意义。
我们同样建立空间xyz坐标系,如下图:
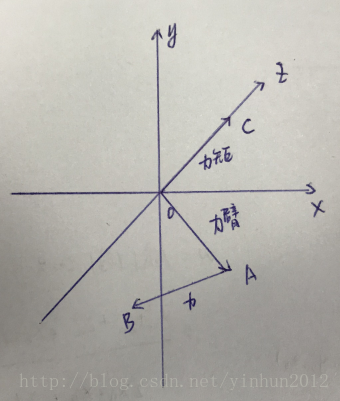
向量OA和AB的叉积OC,OC的属性包括两个
①OC垂直于OA,AB所在的平面(不共线三点确定一个平面)
②OC的向量模长等于OA,AB组成的平行四边形的面积
接下来就要思考怎么计算OC这个向量了,为了直观些,我们继续看下图:
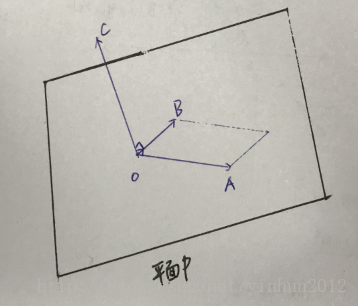
够形象吧,OC这个“力矩”垂直于OB且垂直于OA①,而且模长等于|OA|*|OB|*sin∠BOA②,如下图:

由①我们推算出OC的Z代数坐标分量,那么此时问题就变换成求Z分量了,如下图:

这里我们用xyz基坐标两两的叉积等第三轴的基坐标,这种特殊形式推出OC中z值。
下面我们用程序验证一下,如图:
-
using System.Collections;
-
using System.Collections.Generic;
-
using UnityEngine;
-
-
public
class
CrossMathFunc :
MonoBehaviour {
-
-
public Transform aHead;
-
public Transform aTail;
-
public Transform bHead;
-
public Transform bTail;
-
-
void Start()
-
{
-
//A (a1,a2,a3)
-
Vector3 A = aTail.position - aHead.position;
-
//B (b1,b2,b3)
-
Vector3 B = bTail.position - bHead.position;
-
//用推导公式计算
-
Vector3 crossAB =
new Vector3(A.y*B.z-A.z*B.y, A.z * B.x - A.x * B.z, A.x * B.y - A.y * B.x);
-
-
//用api计算
-
Vector3 apicrossAB = Vector3.Cross(A, B);
-
#if UNITY_EDITOR
-
Debug.LogFormat(
"crossAB = {0} apicrossAB = {1}", crossAB, apicrossAB);
-
#endif
-
}
-
}

上面我们介绍了向量叉积的含义和推导过程,接下来看下两个向量叉积比较形象的示意图,如下:
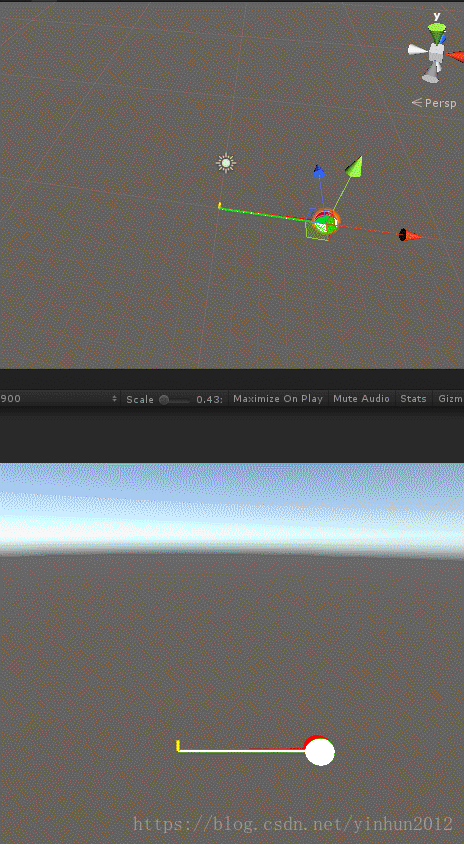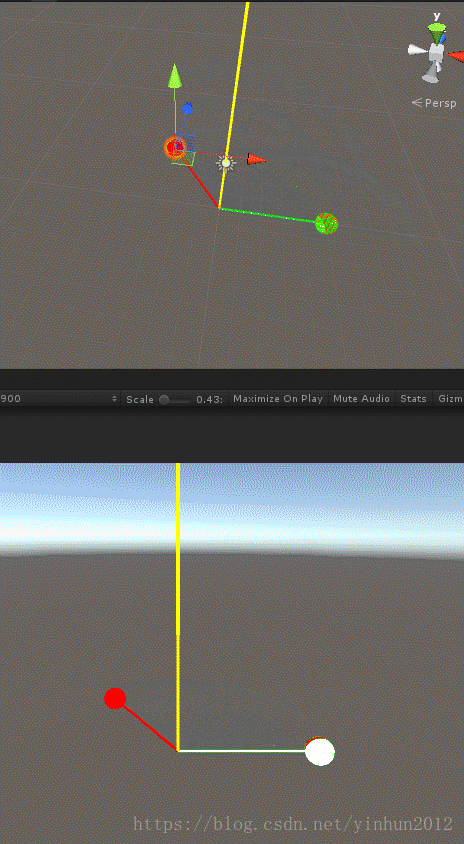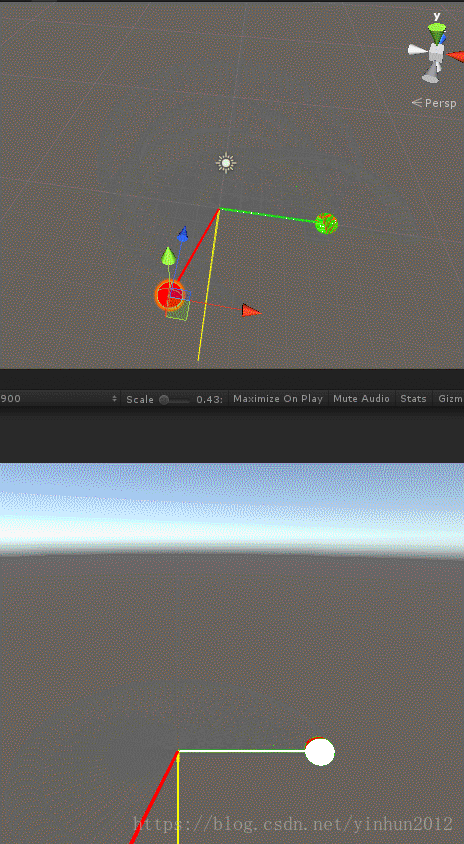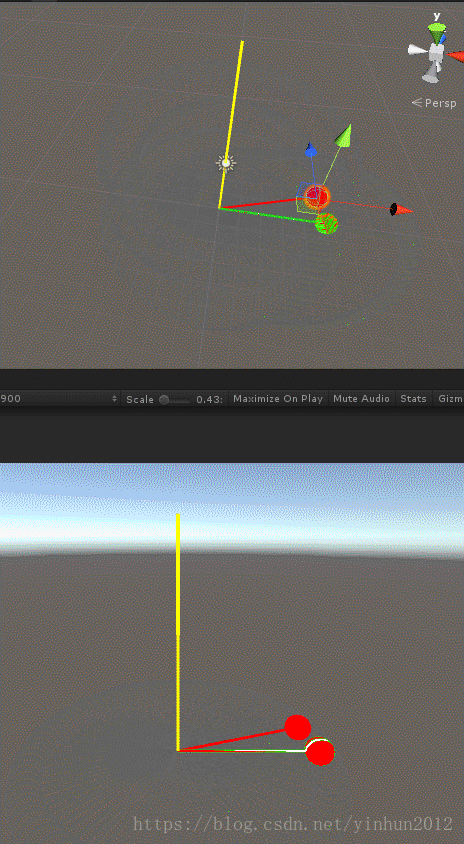
可以看出按照规定的逆时针旋转,两向量夹角在0-180°时叉积向量N“向上”,夹角在180-360°时叉积向量N“向下”。
这个所谓的“向上”和“向下”是一个相对概念,假如我们使用左手坐标系,如下图:
那么向上就是沿着Y轴正方向,向下就是负方向了。
叉积在图形学中应用主要是计算法向量,因为图形学中经常会出现光线反射的问题,叉积提供了我们计算法向量的方法,后面我们继续推导光线反射。








 本文深入探讨了物理中的力矩概念及其数学表达——向量叉积,通过实例解析了力矩的计算方法和几何意义,展示了如何利用Unity进行叉积计算,并讨论了叉积在图形学中的应用。
本文深入探讨了物理中的力矩概念及其数学表达——向量叉积,通过实例解析了力矩的计算方法和几何意义,展示了如何利用Unity进行叉积计算,并讨论了叉积在图形学中的应用。
















 1008
1008

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








