通过改进混合干式冷却塔和太阳能烟囱概念的设计在火力发电厂中利用低品位热能进行电力生产
摘要
本研究提出了一种改进的概念设计,通过结合太阳能烟囱和干式冷却塔来提高典型蒸汽发电厂朗肯循环的热效率。
风能发电的来源包括:冷凝器向进入干式冷却塔的空气排放的废热、太阳辐射以及由注入混合塔的烟道高温烟气在气流中产生的气升泵效应,这是一种新颖的改进。该研究主要针对沙希德·拉贾伊250兆瓦蒸汽发电厂,以确定涡轮机入口处生成气流的速度;采用数值有限体积法对底部直径和烟囱高度分别为250米和200米的干式冷却塔进行了模拟。通过迭代计算不同烟囱壁角度、集热器坡度和基础地面的情况,分析其对输出功率的影响。通过改变混合塔几何参数,风力涡轮机捕获的功率范围从360千瓦到超过4.4兆瓦。获得的结果显示,化石燃料发电厂的热效率最高可提高0.538%。
1. 引言
在许多发电厂中,冷凝器的温水冷却需要使用冷却塔。在水资源有限的地区,广泛使用的冷却塔类型是干式冷却塔。塔内暖空气与外部冷环境空气之间的密度差是自然通风冷却塔中气流产生的促成因素。暖空气从冷却塔排出时携带了大量未利用能量。
近年来广泛发展的最新概念之一是众所周知的太阳能烟囱。太阳能烟囱通常由几个基本部分组成:一个烟囱、一组太阳能集热器和一个风力涡轮机。太阳能烟囱的主要目标是通过加热穿过透明屋顶的空气来产生强大的气流。由于产生的温室效应,被封闭的空气获得大量能量,从而导致烟囱内外空气之间产生密度差。
因此,空气将流向位于塔体起始位置的涡轮机,当空气通过时,涡轮机将发电。
许多研究已用于分析几何结构和日照对太阳能烟囱性能的影响。
Haaf 等人表明,通过增加集热器半径,所产生的输出功率将增加,而发电厂的效率则会降低[1,2]。Pasumarthi 和 Sherif 研究了烟囱高度对空气的质量流量和速度的影响[3,4]。Lodhi 的一项详细研究评估了太阳能烟囱发电厂的预估成本与其效率及最终发电量之间的关系[5]。
Chitsomboon 通过一些研究发现烟囱高度对输出功率的影响,得出结论:功率和效率随烟囱高度的升高而线性增加[6]。此外,他声称塔直径、屋顶高度和日照水平的变化对效率没有影响[7]。在另一项研究中,戴等人展示了电厂规模与输出功率之间的非线性关系,其中电厂规模的增加对较小规模电厂的输出功率改善更为显著[8]。加拿大比尔根和雷诺提出将太阳能集热器建造成倾斜且锥形的部分。这是一个卓越且新颖的想法,因为倾角有助于为集热器提供充足且有效的面积以接收太阳辐射,并有助于提高烟囱入口处的空气速度[9]。最近,丁真表明集热器半径和塔高等几何参数对电厂效率具有显著影响[10]。曹等人从经济角度研究了结构和材料价格在太阳能烟囱成本效益中的作用,并表明更大容量的太阳能烟囱可能更具盈利性[11]。
加农和冯·巴克斯特罗姆 [12]在研究太阳能烟囱中的传热和流体流动模式以及提高相应循环的整体性能方面做出了卓越的工作。鲁普雷希特等人采用计算流体力学方法及其涡轮机设计,提出了额定容量为200兆瓦的太阳能烟囱的结果 [13]。贝尔纳德斯和温雷布通过计算机辅助分析研究,阐明了烟囱的热特性[14]。许多研究人员对引入能够预测太阳能烟囱整体性能的模型表现出兴趣,例如奇特松布恩[7],、施莱希等人 [15],、廷珍等人 [10],、周等人 [16]以及昆斯里苏克和奇特松博姆 [17]。近年来,利用计算流体力学(CFD)程序进行数值方法研究以预测太阳能烟囱发电厂性能的研究迅速增加。帕斯托尔等人对太阳能烟囱发电厂进行了二维数值模拟,并分析了集热器内的温度和流动模式 [18]。
许等人使用了类似的方法[19];这些仿真之间的唯一区别在于储能层和涡轮机模型的设置。明等人[20]对西班牙原型进行了带有三叶片涡轮机的数值模拟,并展示了带有五叶片涡轮机的兆瓦级太阳能烟囱发电厂的模拟结果。他们还通过数值分析研究了通用烟囱形状对太阳能烟囱发电功率的影响[21],,其中表明将太阳能烟囱建造为扩张型烟囱可增加输出功率和总效率,但可能不是一个成本效益项目。昆斯里苏克和奇特松博姆 [17,22],进行了数值模拟,以验证其对太阳能烟囱电站(SCPP)的量纲分析及所提出的无量纲变量。
许多关于倾斜式太阳能烟囱的研究已经开展[23–33];卡拉什等人对倾斜式太阳能烟囱进行了全面的综述研究[23]。他们还通过实验测得了倾斜式太阳能烟囱内部的温度场[25]。利用第二定律分析,昆斯里苏克表明存在一个最优集热器尺寸,可使熵产生最小化并使第二定律效率最大化。他还证明了倾斜式太阳能烟囱在热力学性能上优于传统类型 [24]。此外,李等人已表明,随着收敛型烟囱形状的应用,烟囱效率会降低,而采用扩张型则会提高效率[34]。利用CFD技术,昆斯里苏克和奇特松博姆分析了流动变化对太阳能烟囱发电厂潜力的影响。他们指出,顶部扩张型烟囱可显著增加烟囱底部的动能。倾斜集热棚顶与扩张型烟囱的合理组合所产生的电力可达传统太阳能烟囱发电厂的数百倍 [35]。然而,这些研究中均未涉及流动注入。
邹等人 [36]提出了一种新型的混合冷却塔概念。该概念在传统自然通风系统部件的基础上增加了若干太阳能集热器,用于捕获太阳能。这增强了塔的抽吸能力,与太阳能烟囱和自然通风干式冷却塔相比,显著提高了输出功率和效率。此外,该研究团队在另一项研究中还提出了一种利用太阳辐射辅助的自然通风干式冷却塔的优化方案 [37]。
在最近的研究中,赞迪安和阿什贾耶[38]提出了一种新概念,将干式冷却塔与太阳能烟囱重新组合,通过回收电厂冷凝器排出的废热,并利用该热量加热气流(传统太阳能烟囱仅依靠太阳辐射加热气流),从而产生更多的电能。结果表明,在配备底面直径为250米的干式冷却塔以及高200米、直径50米的混合塔的250兆瓦化石燃料发电机组中,热效率最高可提高0.37%。
本文进行了更多研究,以提高最近提出的混合冷却塔‐太阳能烟囱(HCTSC)概念的效率。本研究取得的显著成果是使火力发电厂效率提高了0.54%,远高于最近研究中报道的0.38% [38]。
第一步中,尝试改进混合塔的一些关键几何参数;为此,研究了混合塔壁面的收敛与扩散对风速的影响;此外,将集热器和基础地面朝中心倾斜,以观察坡度变化对混合系统热效率的影响。
最后,排气热烟气从电厂烟囱注入到混合塔的适当高度,以在通过涡轮机的空气中产生气升泵效应。Hanafi-zadeh 和 Ghorbani[39] 对不同气升泵系统及其概念进行了全面的综述研究。高温烟气在涡轮机上方10米的高度注入混合塔,这是既能获得效率最大提升又可避免对涡轮叶片造成破坏性影响的最低可能高度。使用开发的计算流体力学有限体积法程序,在相同的边界条件下对每种几何情况进行了迭代计算。
2. 案例几何结构
我们的案例几何结构基于伊朗加兹温沙希德·拉贾伊火力发电厂 250兆瓦机组典型的自然通风干式冷却塔,如[38]所示。循环水的特性和热力条件见表1。
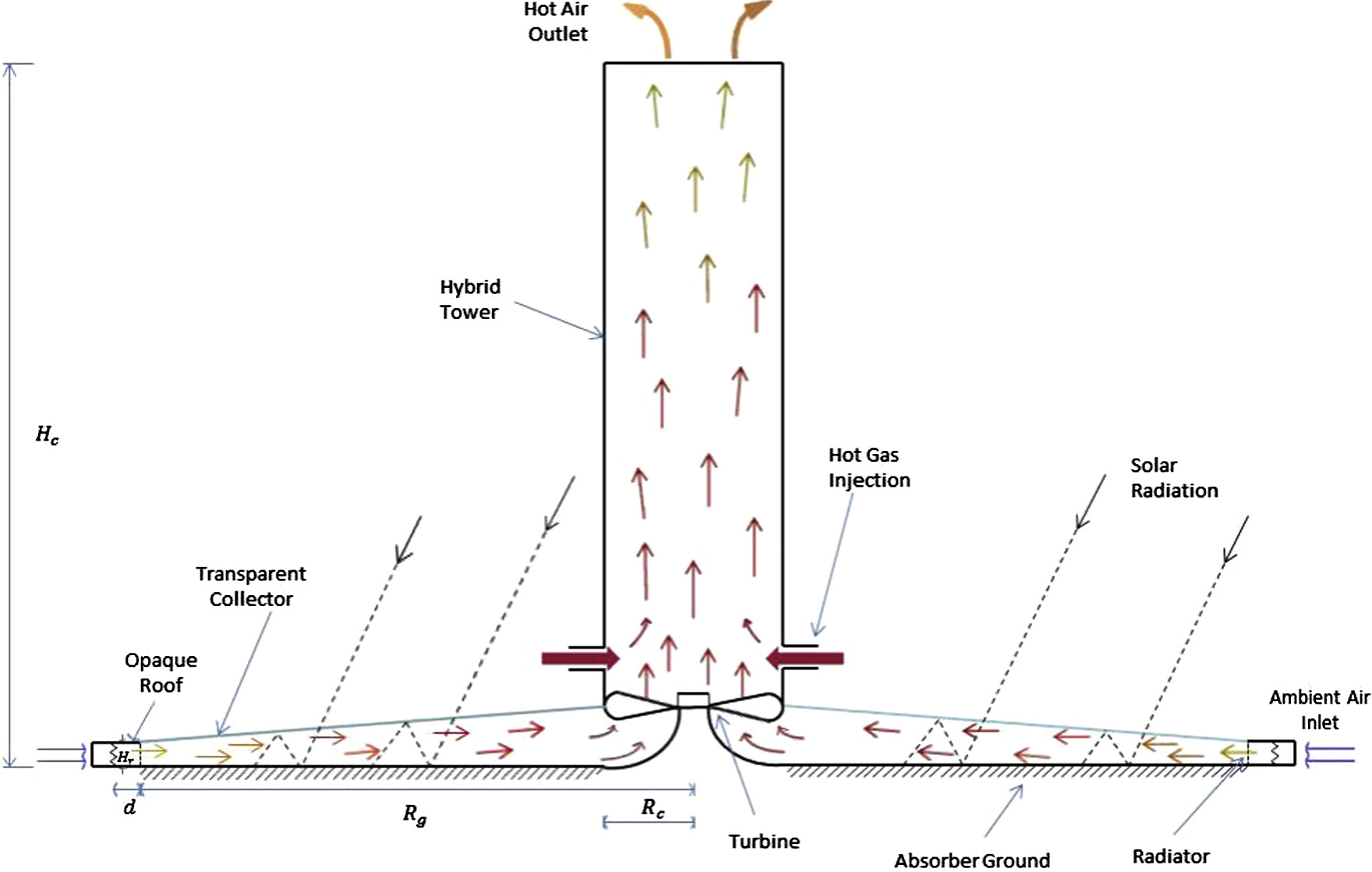
混合系统的布局示意图如 图1 所示。从图中可以看出,外部环境空气从敞开的塔底周边流经换热器(散热器)进入混合塔,冷却在散热器管内循环的冷凝水。随后,空气流经透明(集热)屋顶下方的空间,由于温室效应截留太阳辐射,使空气被加热。此外,空气在涡轮机上方与注入的高温烟气相遇并混合,导致温度和速度升高,同时在混合塔喉部产生抽吸力,从而实现更大的输出功率。
涡轮机。由于浮力效应,气流径向朝系统中心移动,并通过安装在混合塔喉部的风力涡轮机。注入的高温烟气在升高过程中温度逐渐降低,最终被排入大气。
表1 冷却系统中循环水的条件
| 参数 | 值 |
|---|---|
| 循环水流量 ðm³/sÞ | 7 |
| 系统中的水体积 ðm³Þ | 4565 |
| 冷凝器进水温度 (°C) | 60–64 |
| 冷凝器出口水温 (°C) | 48–50 |
当前混合模型相关的所有尺寸均在 表2 中给出。塔高和集热器半径假设与赞迪安和阿什贾耶提出的混合冷却塔‐太阳能烟囱的尺寸相同 [38],,以便通过比较更明显地体现发电量的提升。
为了使干式冷却塔良好运行,进入和离开凝汽器的循环水温度必须保持在适当范围内,以避免发生故障。为此,必须确定屋顶入口高度,使其保持与沙希德·拉贾伊发电厂传统冷却塔中相同的散热器表面积。为了防止地面吸收的太阳辐射对散热器产生不利影响,在屋顶和散热器之间设置了20米的距离,如图1所示。除验证部分外,所有计算均在相同的环境条件下进行迭代,即环境温度,并假设太阳辐射为平均值且恒定不变。

表2 混合系统模型使用的尺寸和部分参数列表
| 参数 | 数值(米) |
|---|---|
| 混合塔塔高 (Hc) | 200 |
| 塔底半径 (Rc) | 25 |
| 玻璃屋顶半径 (Rg) | 100 |
| 注入高度 (Hi) | 22–40 |
| 屋顶入口高度 (Hr) | 9.5 |
| 集热器与散热器之间的距离 (d) | 20 |
| 涡轮机距地面高度 | 12–30 |
3. 数值模拟方法
本研究采用有限体积CFD代码,通过网格划分将空间域离散为有限控制体积。该案例研究的自适应非结构化网格系统包含近5,500,000个网格单元。
假设地面是一个具有 ða ¼ 1Þ的完美吸收体;集热器的不透明表面 s ¼ 0:9被视作具有完全透射率。
集热器屋顶和所有不透明表面均被视为在其长度方向上无热损失的隔离体。
为了确定注入混合塔的高温烟气的流量,采用以下燃烧反应:
$$
C_xH_y + \left(x + \frac{y}{4}\right)(O_2 + 3.76N_2) \rightarrow xCO_2 + \frac{y}{2}H_2O + \left(x + \frac{y}{4}\right)3.76N_2
$$
$$
C_{p0,\text{mixture}} = \sum_{i=1}^{N} c_i C_{p0,i}
$$
其中 N = 组件数量。
$$
c_i = \frac{y_i}{\sum y_j M_j / M_j}
$$
$$
y_i = \frac{n_i}{n_{\text{total}}}
$$
Mi = 分子量 由于x和y的值、燃料质量流量及其分子量可从电厂数据库中获得,因此可以计算出高温气体摩尔流量。利用燃烧产物中各组分的分子量,估算出高温气体质量流量为80.7 千克/秒。此外,测得注入的高温烟气温度约为400 开尔文。在混合概念中,温度是最关键的参数之一,对产生上升运动起着至关重要的作用。显然,比热与温度一样也是一个重要参数,因此通过使用混合物定律计算注入的高温烟气的比热。为了在求解过程中避免两相方程的复杂性,将注入的高温烟气的其他热力学性质设置为与入口空气相似。
根据廷珍等人 [10],我们系统的瑞利数高于 10⁹的临界值,但入口区域。因此,可以假设在流场的几乎所有位置都为湍流;相应地,采用标准k—ε方程来模拟湍流效应。
让我们从连续性、动量和能量方程等基本方程开始,这些方程将被用于该系统。
连续性方程:
$$
\frac{\partial \rho}{\partial t} + \frac{\partial (\rho u)}{\partial x} + \frac{\partial (\rho v)}{\partial y} + \frac{\partial (\rho w)}{\partial z} = 0
\quad (5)
$$
动量方程:
$$
\frac{\partial (\rho u)}{\partial t} + \frac{\partial (\rho uu)}{\partial x} + \frac{\partial (\rho vu)}{\partial y} + \frac{\partial (\rho wu)}{\partial z} = -\frac{\partial p}{\partial x} + \mu \left( \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} + \frac{\partial^2 u}{\partial z^2} \right)
\quad (6)
$$
$$
\frac{\partial (\rho v)}{\partial t} + \frac{\partial (\rho uv)}{\partial x} + \frac{\partial (\rho vv)}{\partial y} + \frac{\partial (\rho wv)}{\partial z} = -\frac{\partial p}{\partial y} + \mu \left( \frac{\partial^2 v}{\partial x^2} + \frac{\partial^2 v}{\partial y^2} + \frac{\partial^2 v}{\partial z^2} \right)
\quad (7)
$$
$$
\frac{\partial (\rho w)}{\partial t} + \frac{\partial (\rho uw)}{\partial x} + \frac{\partial (\rho vw)}{\partial y} + \frac{\partial (\rho ww)}{\partial z} = \rho g \beta (T - T_1) + \mu \left( \frac{\partial^2 w}{\partial x^2} + \frac{\partial^2 w}{\partial y^2} + \frac{\partial^2 w}{\partial z^2} \right)
\quad (8)
$$
能量方程:
$$
\frac{\partial (\rho c T)}{\partial t} + \frac{\partial (\rho c u T)}{\partial x} + \frac{\partial (\rho c v T)}{\partial y} + \frac{\partial (\rho c w T)}{\partial z} = k \left( \frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} + \frac{\partial^2 T}{\partial z^2} \right)
\quad (9)
$$
在考虑将热烟气注入烟囱的影响时,方程(8)中的项 $\rho g \beta (T - T_1)$ 以及方程(15)均起着重要作用。如前所述,已采用k—ε模型来计算湍流的影响。该模型的相关方程可写为如下形式。
$$
\frac{\partial}{\partial t}(\rho k) + \frac{\partial}{\partial x_i}(\rho k u_i) = \frac{\partial}{\partial x_j} \left( \left( \mu + \frac{\mu_t}{\sigma_k} \right) \frac{\partial k}{\partial x_j} \right) + G_k + G_b - \rho \varepsilon + S_k;
\quad (10)
$$
$$
\frac{\partial}{\partial t}(\rho \varepsilon) + \frac{\partial}{\partial x_i}(\rho \varepsilon u_i) = \frac{\partial}{\partial x_j} \left( \left( \mu + \frac{\mu_t}{\sigma_\varepsilon} \right) \frac{\partial \varepsilon}{\partial x_j} \right) + C_{1\varepsilon} \frac{\varepsilon}{k} (G_k + C_{3\varepsilon} G_b) - C_{2\varepsilon} \rho \frac{\varepsilon^2}{k} + S_e
\quad (11)
$$
其中 $ \mu_t $ 在公式(10)中表示湍流黏度,可通过公式(12)计算;
$$
\mu_t = \rho C_\mu \frac{k^2}{\varepsilon}
\quad (12)
$$
在方程(10)和(11)中,$ G_k $ 是由平均速度梯度引起的湍流动能生成,而 $ G_b $ 是由浮力引起的湍流动能生成;这些变量由以下方程获得;
$$
G_k = \mu_t \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right) \frac{\partial u_i}{\partial x_j};
\quad (13)
$$
$$
G_b = g_i \beta \frac{\partial T}{\partial x_i}
\quad (14)
$$
标准 k—ε模型包含多个在表3中给出的经验常数。
最后,当前研究中采用的布辛涅斯克近似模型的热膨胀系数β定义如下;
$$
\beta = -\frac{1}{\rho} \left( \frac{\partial \rho}{\partial T} \right)_p
\quad (15)
$$
需要注意的是,壁面对湍流[40],具有显著影响,且求解变量梯度在壁面附近值较高。因此,在求解控制方程时,采用壁面附近处理至关重要。在壁面附近生成了约30层棱柱层,以确保边界层内至少包含20个节点,从而实现可接受的精度。根据劳nder 和 斯伯丁[41],的建议,本研究采用了赞迪安和阿什贾耶[38]所使用的相同壁面附近处理方法。值得注意的是,改变集热器屋顶坡度、地面坡度或烟囱形状并不会影响所采用的公式;实际上,这些仅会改变网格单元的数量以及求解方程所需的时间。
4. 边界条件
为了计算传递给流经散热器的气流的传热速率,可以使用简单的传热方程,该方程需要散热器管内循环水的物性及其出口和入口温度,如表4所示。此外,传热表面积可通过沙希德·拉贾伊冷却塔的几何尺寸获得[38]。因此,散热器区域的热流密度可通过以下方程获得;
$$
\dot{Q} = \dot{m} C_p (T_{\text{out}} - T_{\text{in}})
\quad (16)
$$
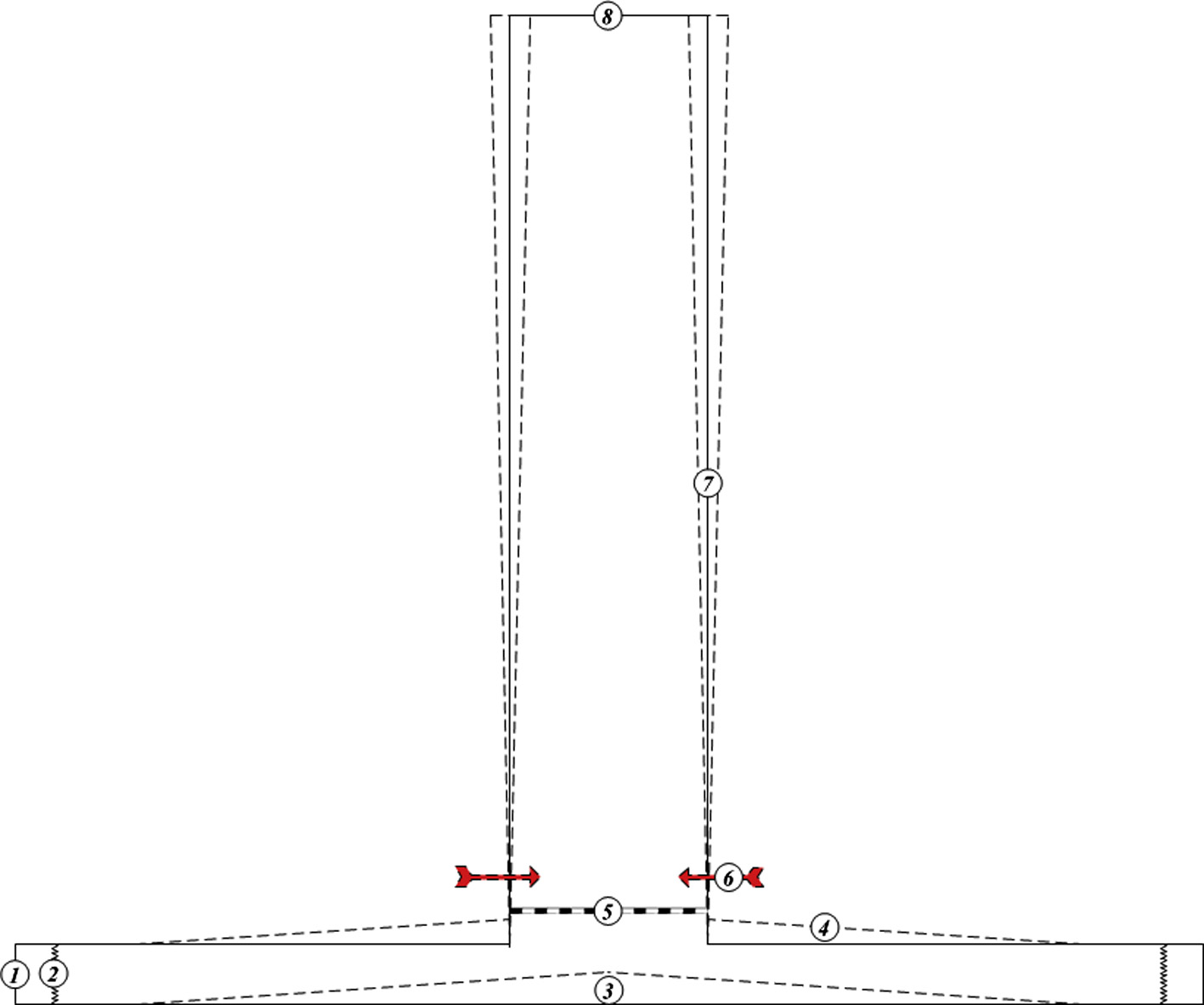
边界条件在表5中给出。此外,边界及其对应的编号在图2中进行了说明。虚线表示变化的边界,以便更清楚地理解几何参数的变化。注意,本仿真中太阳能辐照度设定为600W/m²。同时,仿真在恒定环境温度下进行。根据Gue等人的研究,这一假设是完全可以接受的[42]。此外,进出口压力根据先前的研究设定为0帕[18,19,43–45]。
压降模型已用于对系统中的涡轮机进行建模,将涡轮机视为一个压力显著下降的极薄层。该压降可通过不同方式确定:可将其视为与流速无关,或作为流速的函数。已应用仅含一项的三次多项式来确定通过涡轮机的压降及输出功率。
这种涡轮机的输出功率P_out 由以下方程确定,该方程由Schlaich推荐[46],
表3 标准k‐ε模型经验常数。
| 常数 | 值 |
|---|---|
| C₁ε | 1.44 |
| C₂ε | 1.92 |
| C₃ε | 1.00 |
| Cμ | 0.09 |
| σt | 0.90 |
| σk | 1.00 |
| σε | 1.30 |
表4 冷却水和入口空气特性。
| 参数 | 水 | Air |
|---|---|---|
| 密度 (ρ) | 998.2 千克/立方米 | 1.225 千克/立方米 |
| 比热(Cp) | 4182 焦耳/千克·开尔文 | 1006.43 焦耳/千克·开尔文 |
| 热导率(k) | 0.6 瓦特/米·开尔文 | 0.0242 瓦特/米·开尔文 |
| 黏度 (μ) | – | 1.789 × 10⁻⁵千克/毫秒 |
| 热膨胀系数(β) | – | 0.0033 1/开尔文 |
表5 边界条件
| 边界编号 | 参数 | 值 |
|---|---|---|
| 1 | 环境入口温度 (Tamb) | 295 开尔文 |
| 1 | 入口压力 (pin) | 0 Pa |
| 2 | 散热器热流密度(H) | 51.67 千瓦/平方米² |
| 3 | 地面热流密度 | 0 瓦/平方米² |
| 4 | 集热器热损失系数 (h) | 10 W/m²K |
| 4 | 太阳辐照度 (G) | 600 W/m² |
| 5 | 涡轮压力跃变 | 见公式 (17) |
| 6 | 高温烟气温度 (Tinj) | 400 开尔文 |
| 6 | 热气体质量流量 (ṁ) | 80.7 千克/秒 |
| 7 | 烟囱壁面热流 | 0 瓦/平方米² |
| 8 | 出口压力 (pout) | 0 Pa |

5. 结果与讨论
5.1. 混合塔壁面收敛或发散角的影响
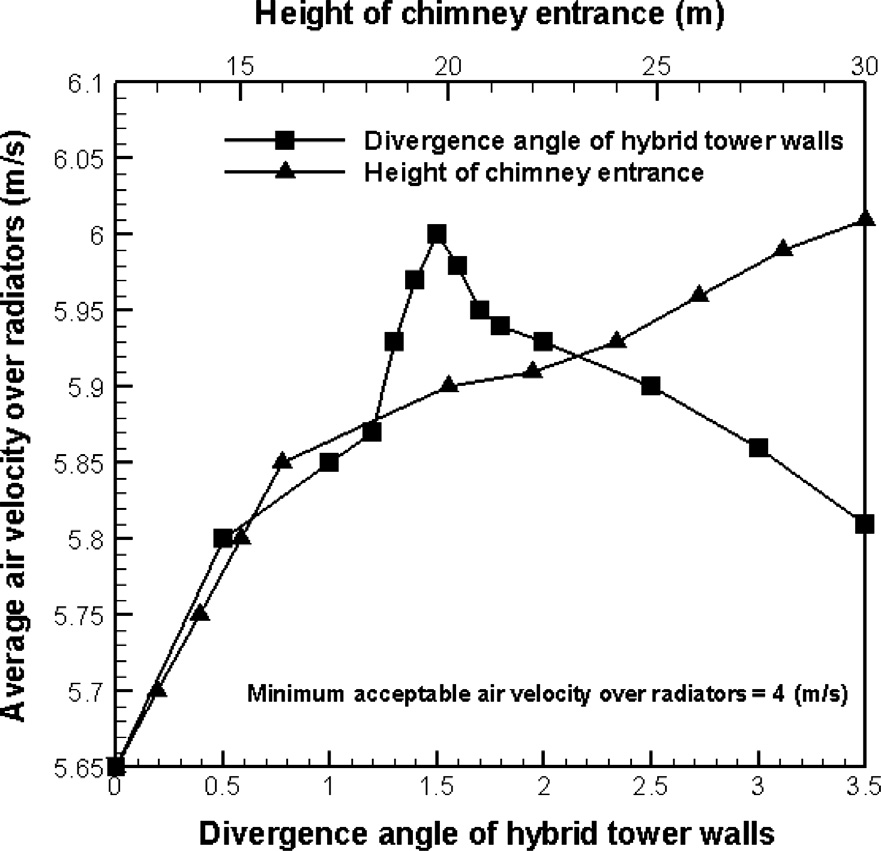
本部分重点研究混合冷却塔‐太阳能烟囱系统的几何参数对涡轮叶片上气流速度的影响;特别是通过改变混合塔壁角度来分析速度和输出功率的变化。为此,塔壁角度从0°变化至3.5°。以下提供表6和表7以展示每种模式下获得的结果。
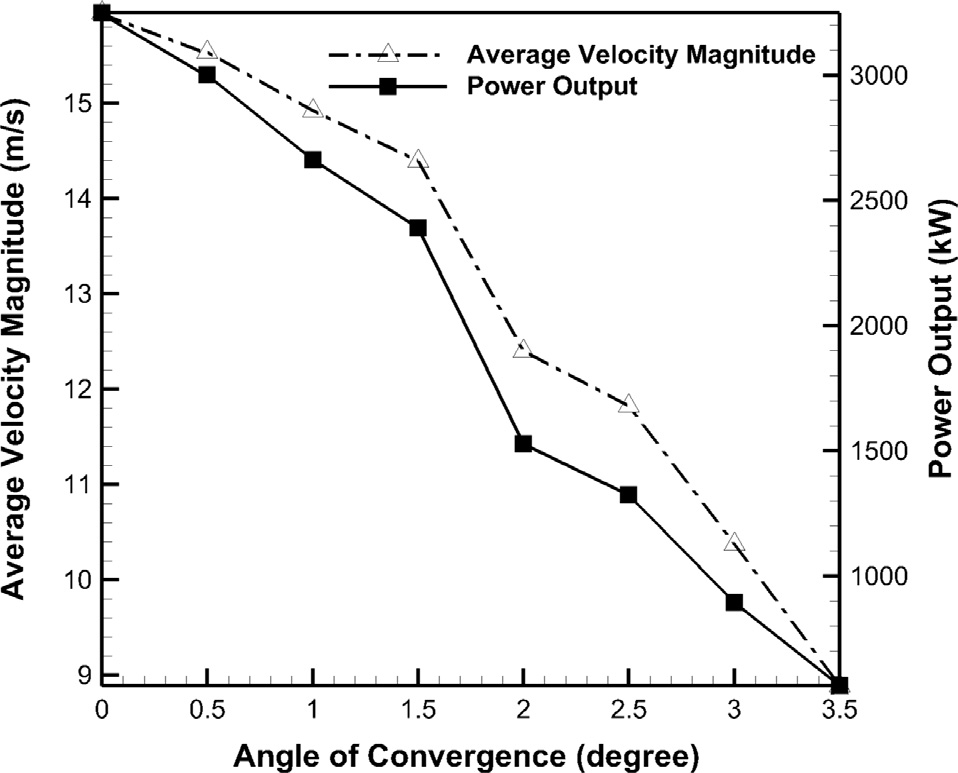
通过观察 图3和图4可以明显看出,当混合塔设计为收敛模式,即混合塔的出口直径小于入口直径时,随着收敛角的增大,涡轮机内平均气流速度迅速降低。这一现象完全符合流体力学理论;由于混合塔直径减小,气流在混合塔出口处的压力会降低,从而导致混合塔内部及涡轮叶片上的气流速度减慢。
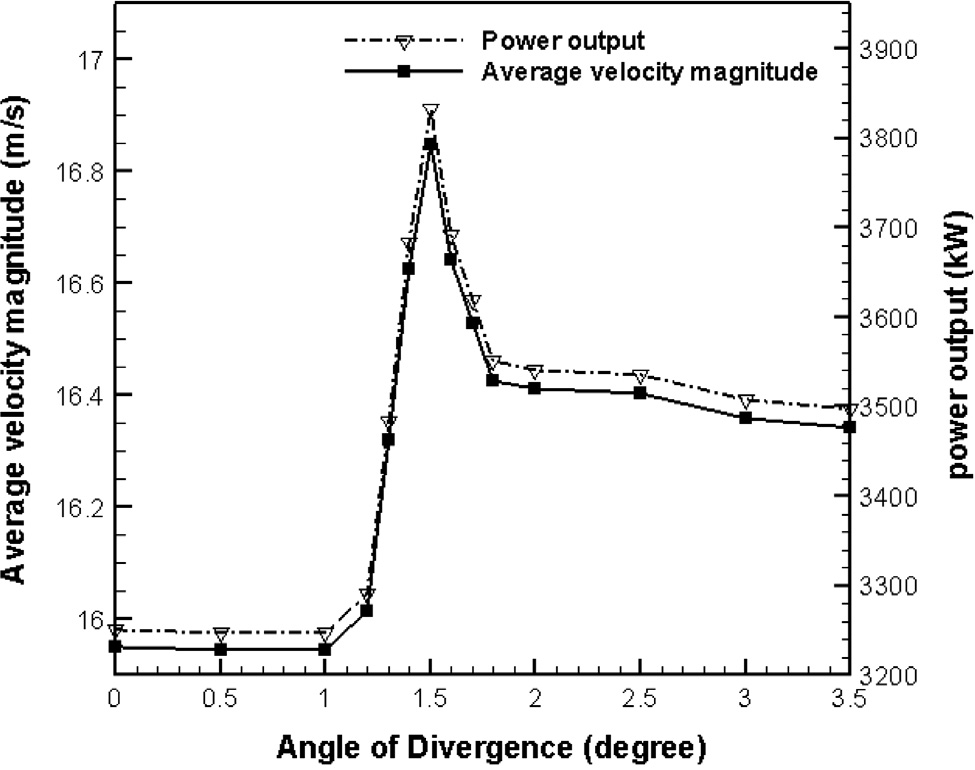
另一方面,混合塔的横截面面积越宽,压力上升越快,从而导致混合塔内部流体运动更剧烈。因此,当混合塔设计为扩散形状时,预期气体流动的平均速度和涡轮机的输出功率都将增加。从表中可以明显看出,当混合塔的扩散程度从0.5°增大到1.5°时,涡轮叶片上的平均流速增加,之后该数值逐渐下降。这种下降源于出口变宽时产生的尾流影响。
表6 混合塔壁发散角对输出功率的影响
| 混合型扩散角 塔壁 (°) | 平均速度在涡轮机 (m/s) | 输出功率 (kW) |
|---|---|---|
| 0.0 | 15.950 | 3250.663 |
| 0.5 | 15.945 | 3247.606 |
| 1.0 | 15.944 | 3246.995 |
| 1.2 | 16.015 | 3290.566 |
| 1.3 | 16.321 | 3482.813 |
| 1.4 | 16.627 | 3682.405 |
| 1.5 | 16.849 | 3831.883 |
| 1.6 | 16.642 | 3692.380 |
| 1.7 | 16.530 | 3618.332 |
| 1.8 | 16.426 | 3550.465 |
| 2.0 | 16.412 | 3541.395 |
| 2.5 | 16.403 | 3535.572 |
| 3.0 | 16.360 | 3507.840 |
| 3.5 | 16.343 | 3496.916 |
表7 混合塔壁收敛角对输出功率的影响。
| 混合塔的收敛角 塔壁 (°) | 涡轮机上的平均速度 (m/s) | 输出功率 (kW) |
|---|---|---|
| 0.0 | 15.950 | 3250.663 |
| 0.5 | 15.533 | 3002.312 |
| 1.0 | 14.921 | 2661.237 |
| 1.5 | 14.394 | 2389.100 |
| 2.0 | 12.402 | 1528.147 |
| 2.5 | 11.824 | 1324.290 |
| 3.0 | 10.371 | 893.6176 |
| 3.5 | 8.8910 | 563.0431 |

5.2. 集热器屋顶坡度对混合冷却塔太阳能烟囱发电量的影响
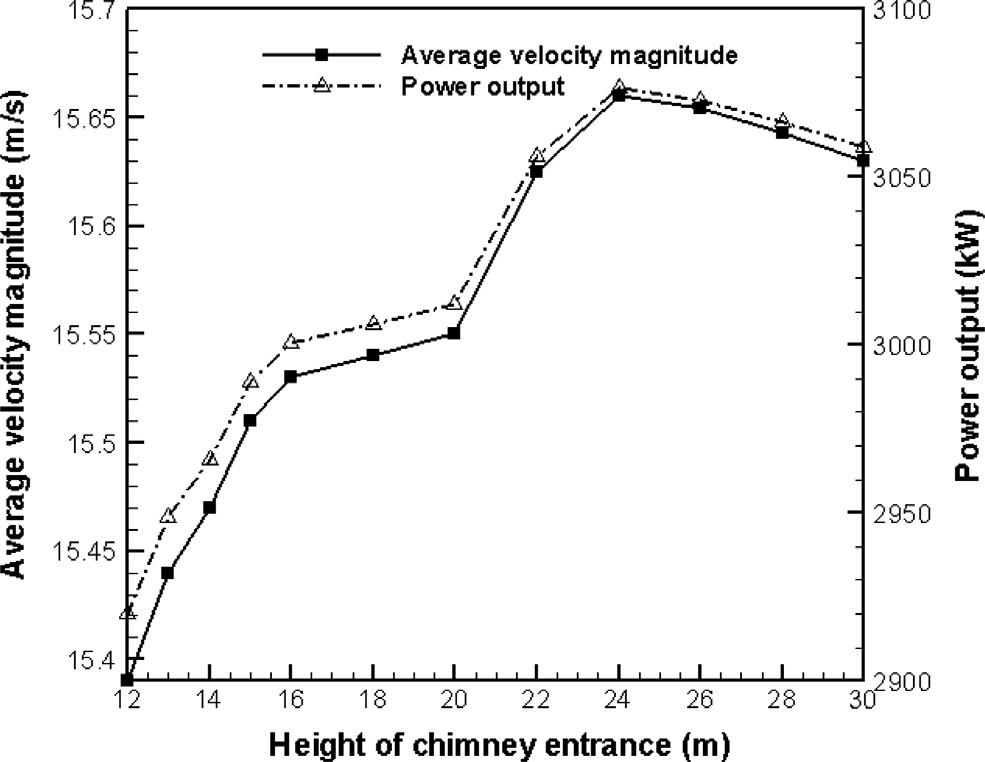
图5 显示了不同集热器屋顶坡度对涡轮叶片上的平均流速及相应输出的影响电力。所有情况均基于平底地面和平稳的环境条件与太阳辐射,具体如下:环境温度, 22 °C;太阳辐照度,600 W/m²。
从结果中可以明显看出,随着屋顶坡度变陡,速度增加,因为空气更容易从集热器流入混合塔。这一现象类似于管道系统中的弯头。流体流动被重定向得越平滑,损失就越小。在HCTSC概念中,随着屋顶坡度的增加,这些损失减少,因此涡轮叶片上的平均流速也增加。此外,集热器屋顶坡度的任何变化都会导致太阳能集热器面积的变化。因此,在具有倾斜集热器的系统中,流体被加热得更多,这一事实增加了流体的能量和速度。正如之前所描述的,在混合塔直径保持不变的情况下,输出功率与空气通过涡轮机的速度成正比。
如图5所示,发电量的这种改善将不再出现,并且在烟囱入口高度为24至26米之间时,可以观察到速度和发电量下降。这一现象可以通过两种方式解释。首先,随着集热器屋顶坡度的增加,在集热器出口区域附近可能会形成尾流;因此,大尺度涡旋可能导致较大的损失。这一问题在发散角超过14°的缩放喷嘴中也存在。其次,通过计算集热器出口和烟囱入口的流动截面积,显然在本研究涉及的各种情况下,前者的值大于后者。因此,当烟囱入口高度增加时,气流会经历突然收缩,这可能会导致较大的损失,而在烟囱入口高度较高时,这些损失将变得显著。
通过将屋顶坡度增加到10.91°,可获得近3077千瓦的电力(相比1°时的2900千瓦提高了约5%)。根据图4,塔入口的最佳高度为24米。因此,在考虑涡轮机与喷射喷嘴之间必需的最小距离(以防止注入的高温气流对涡轮叶片造成破坏性损害)后,如前所述,注入高度设定为34米,即位于涡轮机上方10米处。
5.3. 地面基础坡度对混合冷却塔太阳能烟囱发电量的影响
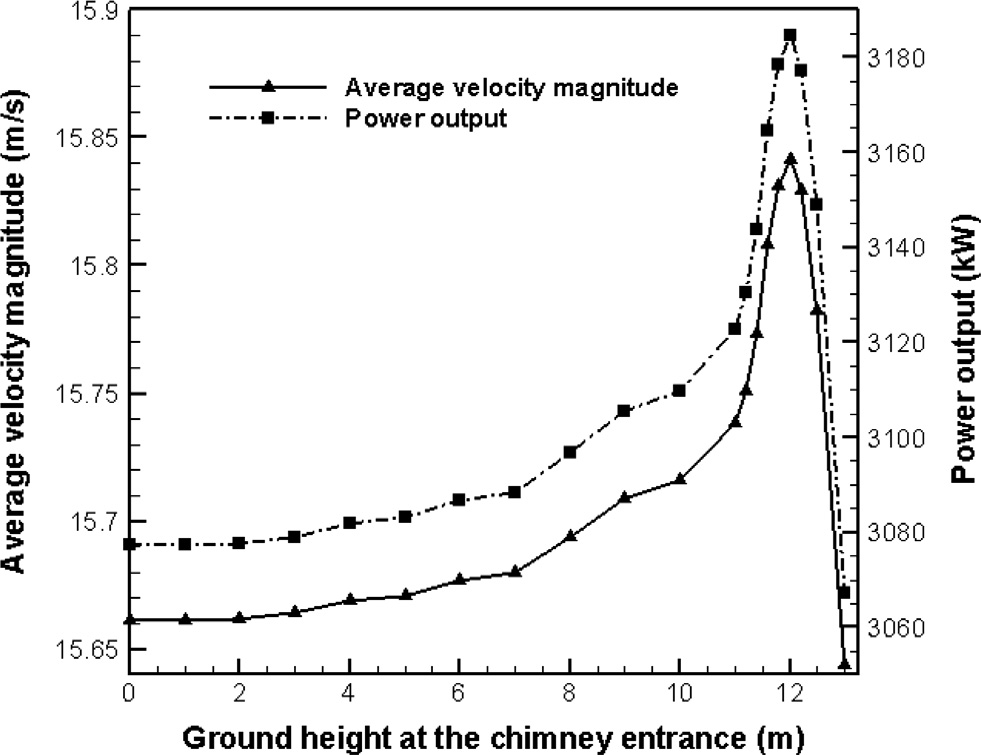
鉴于集热器屋顶坡度对最大可获得输出功率的改善效果,此处针对不同的基础地面坡度(范围从 0°到12.2°)进行了模拟。图6 显示了在烟囱入口处不同基础地面高度下,涡轮机上的平均速度大小及其相关输出功率的变化。边界条件假设与第5.2节相同。与之前关于屋顶坡度的部分类似,图6显示,从开始到倾斜角为8.34°时,速度和发电量仅有轻微提升。然而,在此之后,当倾斜角介于8.34°和9.1°之间时,平均速度和电力输出显著上升;随后,当地面坡度从9.1°变化到9.83°时,出现突然下降的趋势。这主要是由于压力损失突然增加,导致基础中心区域前方的上游流动动量减少,即比值
烟囱入口截面积与散热器截面积之比降低到压力下降超过流动动量的程度。
因此,可以得出结论,9.1°的倾斜角是获得最大可能输出功率 3184千瓦(相比平底地面3077千瓦的输出功率约提升了3.5%)的最佳几何条件。如图6所示,该倾斜角在烟囱入口处对应的地面高度为12米。需要指出的是,注入高度和烟囱入口高度仍分别为34米和24米,因为基础地面显然与此无关。
5.4. 热烟气注入
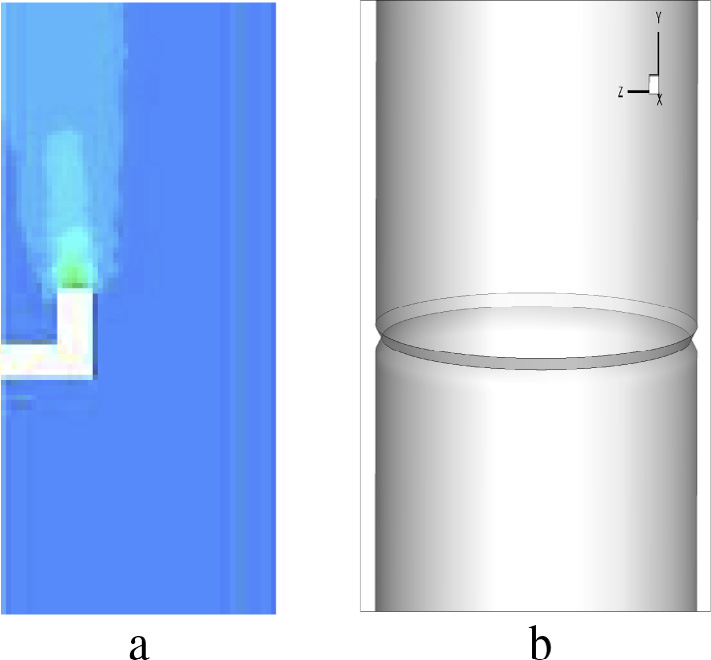
通常,将高温烟气注入烟囱主要有两种方式:使用单射流或采用周边注入;这些结构在图7中进行了示意图表示。使用单射流几乎不会增加涡轮机处的速度。这可能是由于使用单射流时混合过程效率较低所致。因此,本研究采用了周边注入方式。
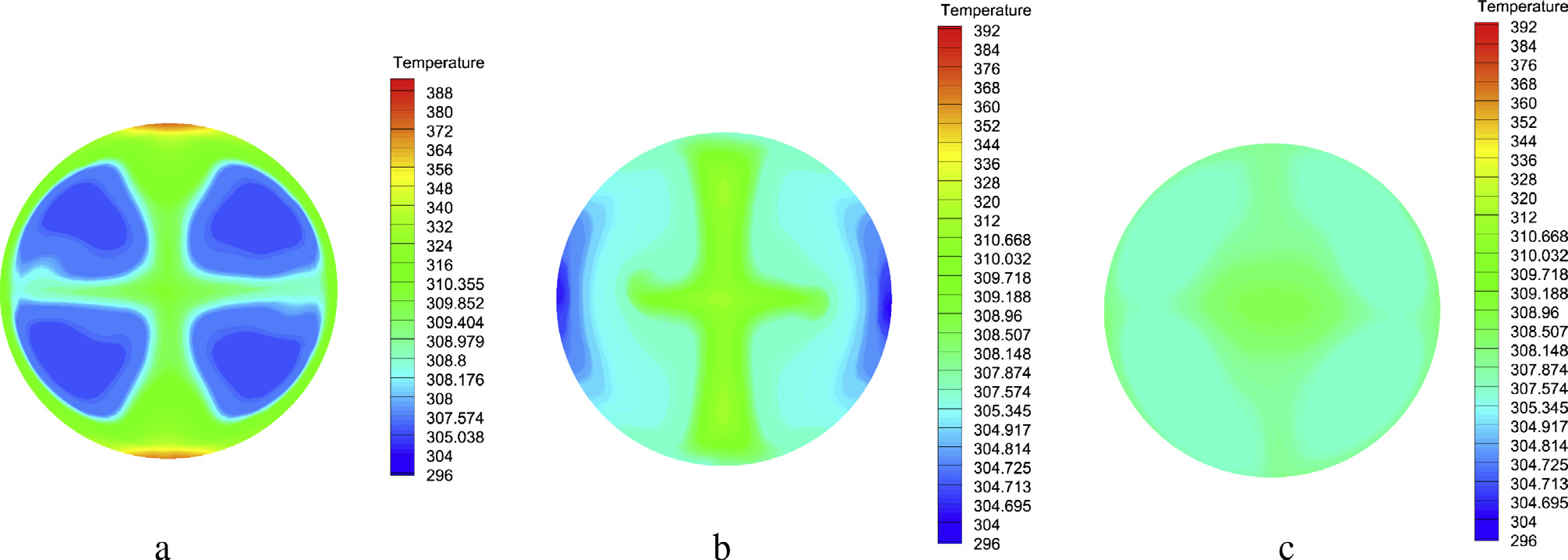
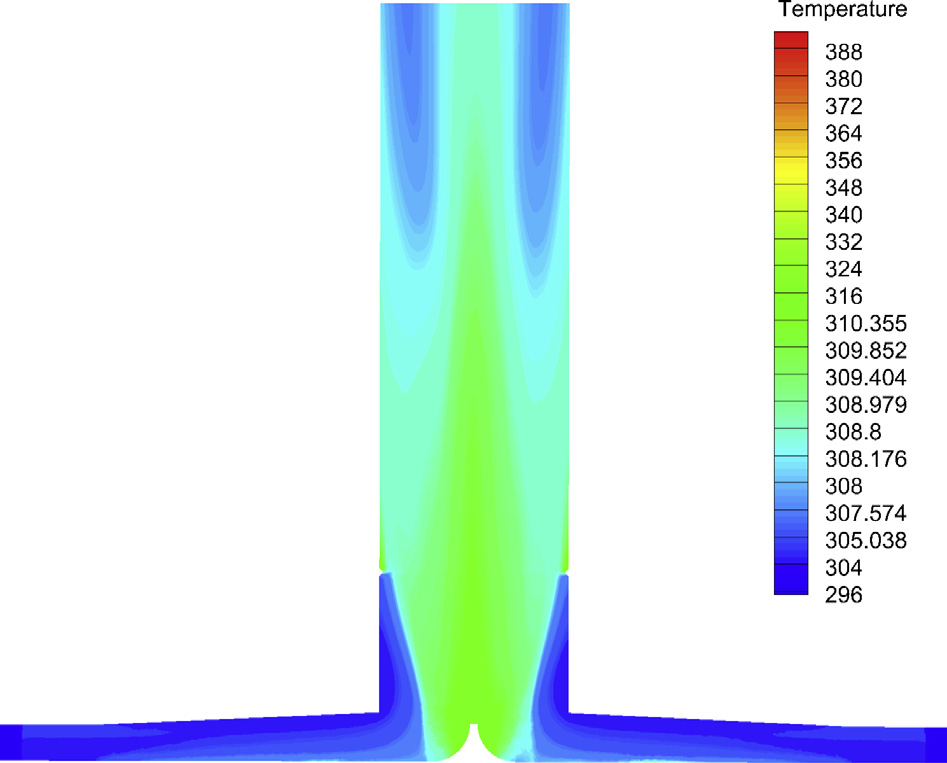
图8 显示了出口附近的流动在热烟气注入前和注入后的温度等值线。从这些图中可以明显看出,热气体的注入在一定距离内改变了烟囱内的流动模式。在注入区域之前,温度似乎几乎是均匀的。然而,注入的影响在一定程度上仍可观察到。通过比较图8a和b,可以清楚地看出,热空气流从烟囱入口开始就已塑造了整体的流动模式。由于气体是从塔的周边注入的,因此靠近塔壁处的温度较高。热气体比冷气体具有更大的浮力,更容易上升。如果没有气体注入,沿烟囱的温度将保持均匀,如 图8c所示。
热烟气注入的影响也可以在 图9和图10中看到。根据 图9,从集热器来的较冷空气仅到达注入点,在此区域之后温度上升,导致气流以更高速度运动。这种热气体带动周围的较冷空气,并由于对称性以及烟囱壁面附近的剪切应力,气流沿塔中心上升,使温度等值线呈现如 图8a 所示的形态。然而,在经过一定距离后,由于高温烟气与较冷空气的混合,烟囱横截面上的温度梯度逐渐减小。
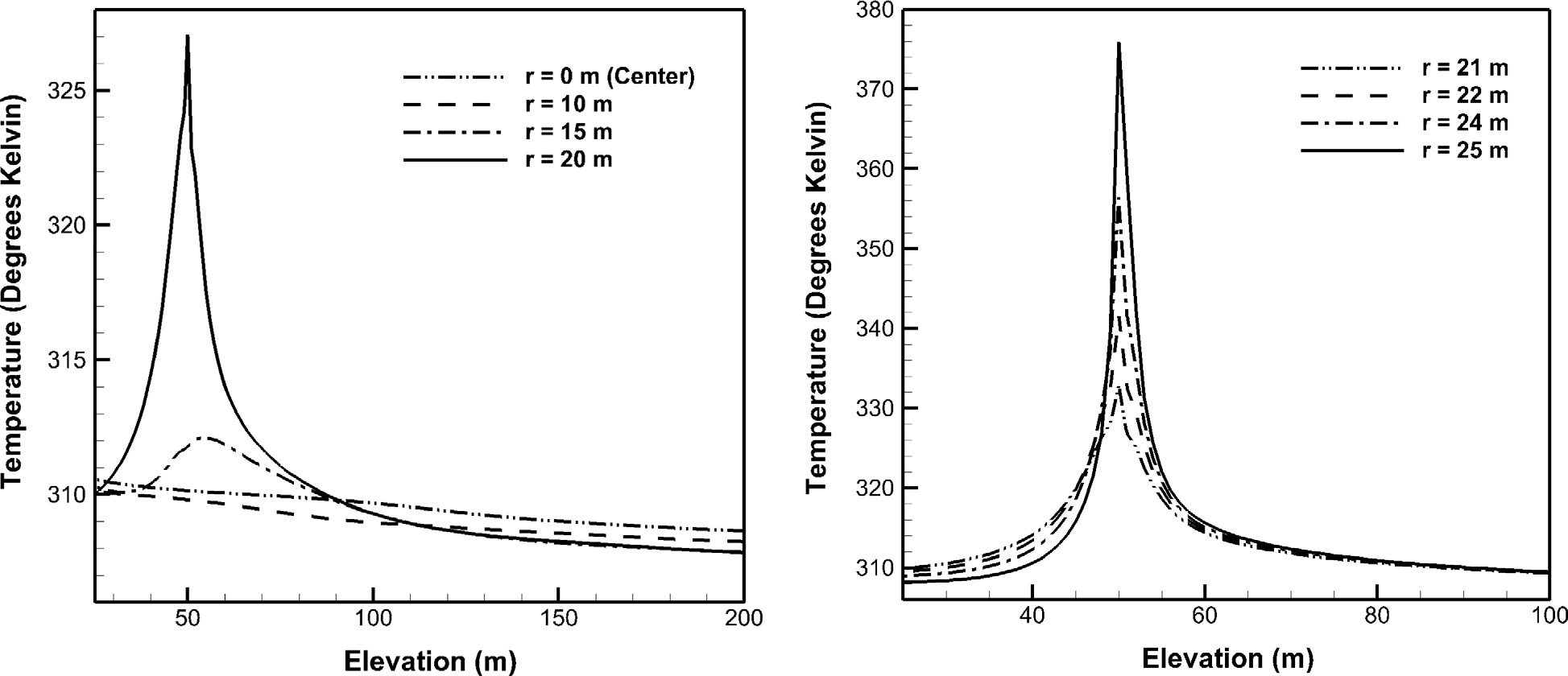
图10 显示了沿烟囱不同径向位置处气流的温度变化。通过分析该图可以得出,热烟气注入首先提高了靠近烟囱壁面各点的温度;随着向烟囱出口方向移动,温度梯度逐渐降低,直至出口区域几乎达到均匀温度。需要注意的是,本案例中特别将注入高度设定为50m,以便仅展示注入的影响,因为涡轮机的存在可能会轻微改变流动模式和温度分布。
 单射流和 ( b ) 均匀周边。)
单射流和 ( b ) 均匀周边。)
5.5. 冷却系统运行限制
值得注意的是,混合冷却塔、太阳能烟囱和烟囱系统各自独立完成其任务也具有重要意义。干式冷却塔的主要任务是降低从发电厂冷凝器进入散热器的入口温水的温度。因此,应考虑相关参数,以防止出现影响冷却塔高效运行的任何可能违规情况。例如,散热器从循环水中吸收的热量不应减少。
最重要的是,混合装置中的任何几何变化都会改变通过散热器的平均空气速度。考虑到散热器上的平均空气速度应保持在朗肯循环规定的限值以上,性能冷却要求,对设计者而言,显然有必要检查此条件是否满足。
根据沙希德·拉贾伊冷却塔内气流平均速度的变化,沙希德·拉贾伊冷却塔散热器部分的流速略高于4米/秒。因此,这种新型混合系统必须提供接近该限值或适当更高的入口速度。
图11 显示了新系统中散热器上空气速度值的变化。如该图所示,散热器上的平均空气流速足够大,可确保冷却系统的正常运行。
6. 改进设计条件
在本节中,总结了各部分中产生最高效结果的参数值。所述参数如 表8所示。
发电厂的热效率定义为:
$$
\eta = \frac{\text{electrical output power}}{\text{input energy}} = \frac{\text{fossil fuel power output} + \text{hybrid power output}}{\text{gross fossil fuel input power}}
\quad (18)
$$
请注意,本例中总化石燃料输入功率大约是输入太阳能的二十倍。因此,为了便于与先前的研究进行比较,在计算发电厂热效率时未考虑输入太阳能。然而,当发电厂的容量与输入太阳能相当的时候,这可能成为一个重要的因素。本文以沙希德·拉贾伊250兆瓦、30%效率(无混合冷却塔、太阳能烟囱和烟道系统)的典型机组为例。根据每种情况下计算出的输出功率,将额外产生的电力加到热电厂的额定输出功率( 250兆瓦)上,然后计算混合系统的新型效率。显然,采用这种创新的混合系统后,发电厂的热效率得到了显著提高。输出功率为4489.4千瓦,这是一个非常出色的成果,可使250兆瓦热电厂的效率提高达0.538%。与赞迪安和阿什贾耶[38],所获得的效率相比,提升了0.168%,这是一项巨大的成就。
表8 来自前几节的最有效值。
| 混合塔壁角度(°) | 注入高度(米) | 塔入口高度(米) | 混合塔直径(米) | 基础地面坡度(°) | 输出功率 ( kW ) |
|---|---|---|---|---|---|
| 1.5(发散) | 34 | 24 | 50 | 9.1 | 4400 |
7. 数值结果验证
7.1. 数值结果验证与实验结果的对比
首先,对西班牙原型的几何结构和边界条件 [2]进行了建模并采用数值方法求解,以验证本研究中采用的方法。根据该实验工作的结果,当太阳辐照度为1000 W/m²,时,烟囱入口处的迎风风速必须为15米/秒,集热器内的温升为20开尔文。桑吉等人也对该原型进行了重新建模,以验证其解法 [45]。本研究的结果、他们的数值工作以及实验结果均示于 表9。
我们的数值方法与文献之间似乎有较好的一致性。然而,仅展示两个参数不足以验证本研究的有效性,因为与传统类型相比,本研究增加了倾斜集热器、屋顶、烟囱壁面以及热烟气注入等多个改进。因此,以下部分将被考虑以确保本研究的有效性。
表9 本研究与关于西班牙原型的其他数值和实验研究的比较
| 研究 | 温度升高 (K) | 迎风风速 (米/秒) |
|---|---|---|
| 实验研究 | 20 | 15 |
| 桑吉等人进行的数值研究 | 20.25 | 15.05 |
| 当前研究 | 20.22 | 15.06 |
7.2. 沿烟囱的相对静压变化
图12 显示了烟囱内相对静压的变化情况;注意,某一点的相对压力定义为该点压力与环境压力之间的差值。沿涡轮机的压力降可以很容易地识别出来。然而,由于热烟气注入,压力分布并未出现任何突变。这表明,与涡轮机的存在相比,热烟气的注入对系统压力没有产生显著影响。相反,温度在注入点附近发生了显著变化,而涡轮机对温度未引起明显改变。
廷珍等人[10]得出的结果完全支持并证实了图12中所示的结果。他们计算了不同条件下沿烟囱相对静压的变化集热器半径的值。关于集热器半径为120m的一个案例,也获得了相同趋势,该结果由[10]得出,并且结果之间具有良好的一致性。此外,廷珍等人[10]已通过解析方法证明,相对静压沿烟囱呈负值分布,并且与高度呈线性关系。这种线性关系在图12中也可以清楚地看到。
7.3. 烟囱沿线的温度变化
烟囱长度方向上烟囱中心处的图13显示了 的变化。根据该图, 沿烟囱高度逐渐降低;Patel 等人[44]的研究也发现了相同的趋势。根据他们的报告,周等人[47]也获得了相同的结果。
7.4. 塔面积变化的影响
昆斯里苏克和奇特松博姆研究了塔流道截面积随高度变化的影响 [35]。他们得出结论:扩张型塔能够提高速度和动能,可用于增加系统的输出功率。然而,他们并未对收缩型烟囱得出相同的结论。本研究也获得了与此相同的结论。
此外,Patel 等人研究了几何参数对太阳能烟囱电站(SCPP)[44]性能的影响。他们得出结论,扩张型烟囱塔确实可用于提高输出功率。他们还表明,该系统存在一个最佳扩张角,这与当前研究的结论一致。然而,他们提出的该参数值为 2° ,与本研究获得的1.5°略有不同。这可能是由于两个案例研究中几何参数存在微小差异所致。
7.5. 环境温度的影响
最后,图14 展示了环境温度对西班牙原型系统性能的影响。Guo 等人也获得了相同的结果。[42]。每种情况下的输出功率值仅有微小差异,这可能是由于本研究在涡轮机建模时所做的假设所致。他们在研究中对涡轮机压降使用了常数值,而本研究则采用多项式函数来描述压降与空气速度之间的依赖关系。然而,环境温度对混合系统的性能影响可以忽略不计。这可能是因为大量能量被添加到系统中,这些能量来自塔内散热器和注入的高温烟气。相比之下,赞迪安和阿什贾耶之前的研究并未显示出随着环境温度升高而输出功率下降的现象。
8. 结论
本文提出了一种新设计,将太阳能烟囱、热蒸汽电厂干式冷却塔和烟道(HCTSC)融合为一种新型电厂概念。该模型基于赞迪安和阿什贾耶的典型尺寸和条件进行设计[38],实际上是沙希德·拉贾伊250兆瓦蒸汽发电厂和曼萨纳雷斯太阳能烟囱的重新设计。随后,建立了包含太阳能集热器、热气体流注入、冷却塔散热器和风力涡轮机在内的混合系统的数值模拟。通过研究不同混合塔壁角度以及集热器屋顶和基础地面坡度对输出功率的影响,观察到了发电能力的提升。最后,研究了在烟道注入高温烟气的情况下,这些参数对混合系统(HCTSC)输出功率及整个化石燃料发电厂效率的影响。
结果表明,在相同环境条件下,与Zan-dian和Ashjaee提出的混合系统相比,新型混合系统的输出功率显著提高。研究结果表明, HCTSC系统最大可实现4.489兆瓦的输出功率,使沙希德·拉贾伊250兆瓦化石燃料发电厂的热效率提高了0.538%。
因此,该设计证明了能够回收烟道中高温烟气以及散热器散发到大气中而未得到有效利用的热量,并防止过量温室气体的产生。最后,在未来的研究中考虑涡轮机效率变化的影响可能是一项良好的改进,且具有一定的意义。此外,预测结果表明,系统的几何参数存在一个最佳条件。因此,强烈建议在未来的研究中同时研究集热器、地面和烟囱壁面倾斜的影响,并对此案例应用适当的优化方法。
 混合冷却塔提升火电效率
混合冷却塔提升火电效率




















 1402
1402

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








