poj1681Painter's Problem 增广矩阵消元法错误水过版

最新推荐文章于 2024-11-27 10:15:23 发布

原创最新推荐文章于 2024-11-27 10:15:23 发布 · 700 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#acm #消元法 #poj

acm 同时被 2 个专栏收录

33 篇文章

订阅专栏

消元法

2 篇文章

订阅专栏

本文探讨了一个关于改变开关状态的问题，通过使用消元法求解最少的操作次数，使所有开关达到一致状态。虽然提供的代码存在局限性，但适用于特定的数据集。

Painter's Problem

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 5519		Accepted: 2660

Description

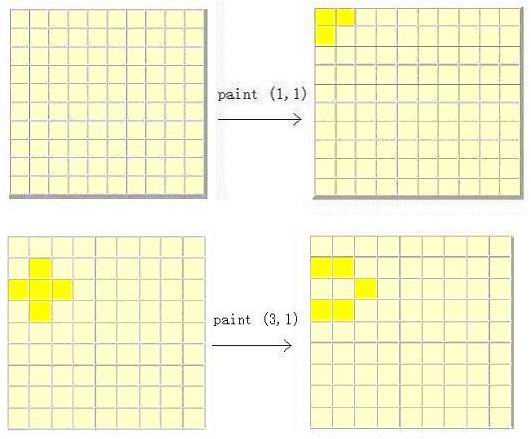
There is a square wall which is made of n*n small square bricks. Some bricks are white while some bricks are yellow. Bob is a painter and he wants to paint all the bricks yellow. But there is something wrong with Bob's brush. Once he uses this brush to paint brick (i, j), the bricks at (i, j), (i-1, j), (i+1, j), (i, j-1) and (i, j+1) all change their color. Your task is to find the minimum number of bricks Bob should paint in order to make all the bricks yellow.

Input

The first line contains a single integer t (1 <= t <= 20) that indicates the number of test cases. Then follow the t cases. Each test case begins with a line contains an integer n (1 <= n <= 15), representing the size of wall. The next n lines represent the original wall. Each line contains n characters. The j-th character of the i-th line figures out the color of brick at position (i, j). We use a 'w' to express a white brick while a 'y' to express a yellow brick.

Output

For each case, output a line contains the minimum number of bricks Bob should paint. If Bob can't paint all the bricks yellow, print 'inf'.

Sample Input

2
3
yyy
yyy
yyy
5
wwwww
wwwww
wwwww
wwwww
wwwww

Sample Output

0
15

题意：poj1222开关问题的一般化情况，改变某一个开关的状态会影响周围四个开关的状态，让你求最少的改变次数，使得所有的开关都为y

思路：跟poj1222一样的消元法，但是……

上次的poj1222的系数矩阵是固定的，消元后正好是一个满秩矩阵，所以不用考虑无解的情况，也不用考虑回带答案，而这个题目很有可能会无解，很有可能要回带答案……

上次完全没有考虑到这些情况……竟然就这么水过去了……

代码

#include <stdio.h>  
#include <string.h>  
#include <algorithm>  
using namespace std;  
int a[35],x[230],map[20][20],b[230][230];  //b:系数矩阵的增广矩阵  
    int i,j,k,m,n,t;  
  
int gauss(int n)  
{  n=n*n;
 int flag,c,i,j,k;  
 for(k=1,c=1;k<=n,c<=n;c++,k++)   //k枚举行，c枚举列  
   {flag=0;
    for(i=k;i<=n;i++)  
      if(b[i][c]==1){flag=1;break;}  
    if(flag==0){k--;continue;}  
	if(i!=k)  
      for(j=1;j<=n+1;j++)swap(b[i][j],b[k][j]); 
	
    for(i=1;i<=n;i++)  
     if(i!=k && b[i][k]==1)  
      for(j=1;j<=n+1;j++)b[i][j]=b[i][j]^b[k][j];      
   }
   for(i=k+1;i<=n;i++)
    if(b[i][c]!=0)return 0;
   for(i=n;i>=1;i--)          //讲道理这个地方是错误的，不一定自由未知量全是零的时候正好是最优解，但是题目数据弱也就这么水过去了…… 
	{
		x[i]=b[i][n+1];
		for(j=i+1;j<=n;j++)
		  x[i]^=(b[i][j]&&x[j]);
	  }  
  return 1;   
}  
  
  
int main(int argc, char const *argv[])  
{     
    char ch;  
    scanf("%d",&t);  
    for(int t1=1;t1<=t;t1++)  
    { memset(a,0,sizeof(a));  
      memset(x,0,sizeof(x));  
      memset(b,0,sizeof(b));
	  scanf("%d",&n); 
      for(i=1;i<=n;i++)       //构建矩阵  
      {getchar();
        for(j=1;j<=n;j++)  
            {scanf("%c",&ch);
			 if(ch=='y')map[i][j]=0;
			   else map[i][j]=1;  
             b[n*i-n+j][n*n+1]=map[i][j];  
             b[n*i-n+j][n*i-n+j]=1;  
             if(i>1)b[n*i-n+j][n*i-2*n+j]=1;  
             if(i<=n-1)b[n*i-n+j][n*i+j]=1;  
             if(j>1)b[n*i-n+j][n*i-n+j-1]=1;  
             if(j<=n-1)b[n*i-n+j][n*i-n+j+1]=1;   
              }  
       }
	  int cnt=0;
      int f=gauss(n);
	  if(f==0)printf("inf\n");
	  else
	   {for(i=1;i<=n*n;i++)  
        if(x[i]==1)cnt++;  
        printf("%d\n",cnt);  
	  }
	  
      
  
    }  
    return 0;  
}

但是这个解法还是错的，这个代码里自由未知量假设的全是零，但是事实上不一定自由未知量全为0的时候1的个数最小，还需要枚举自由未知量的状态来求最优解……

但是题目数据太弱也就这么水过去了……

下次补上正确解法