轴平移越障轮机构设计与分析

通过轴平移的越障轮机构的力与操作分析

摘要

坡道、台阶和不规则地面等障碍在家庭、办公室及其他公共场所中普遍存在，这些障碍常常限制了使用移动辅助设备人群的日常活动。为了扩大他们的活动范围，提出了一种通过减小水平爬升力来实现爬台阶的轮式机构，并将其应用于电动轮椅中。该机构可提高使用者的自主性，从而减轻护理人员和医务人员的身心负担。具体而言，所提出的电动轮椅爬台阶机构依赖于通过偏移轮子的旋转轴来实现爬台阶功能。本文详细介绍了该偏移机构及其力分析。

关键词 ：辅助机器人 ⋅ 轴平移 ⋅ 爬台阶 ⋅ 轮椅

1 引言

在日常生活中，我们经常遇到门槛、不平整表面和坡道。依赖轮式辅助设备（如轮椅[1]和助行器[2]）的人们常常受到这些障碍的阻碍，导致其日常活动受限。已有许多研究致力于解决这些问题。例如，已设计出各种辅助装置，可附加到现有的轮椅上[3]。其他研究则开发了具有增强的爬楼能力的替换部件。其中一些替换轮子将多个较小的轮子组合成一个较大的轮子装配[4]。在替换部件方面，已考虑更换后轮和前轮，并研究了使用履带替代轮子的方案[5]。此外，一些设备从设计之初就针对爬台阶功能进行了专门设计[6]。这些研究中的设备存在多种缺点，例如高成本、庞大体积、重量大和高复杂度。通常很难将这些设备集成到现有的低成本辅助设备中。

本文提出并实现了一种可集成到现有辅助设备中的轮式机构。具体而言，该轮式机构的设计思想是通过将轮子的旋转轴从轮心垂直偏移来增大其滚动半径。如图1所示，该偏移过程产生了伪轮直径。因此，该轮式机构能够实现两种运动：第一种是正常滚动，第二种是专用于爬台阶的独立运动。爬台阶动作旨在减小爬台阶所需的水平力。本文分析了所提出的机构的实际方面，例如水平力和操作。本工作的主要贡献是（1）实现了爬台阶单元；（2）该单元能够实现可靠的爬台阶运动。由于该轮式机构易于集成且结构紧凑，预计可应用于多种移动辅助设备。

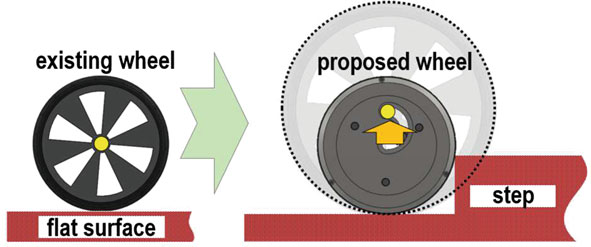
旋转轴用双轮机构

所提出的爬台阶解决方案的关键思想是通过垂直偏移轮子的旋转轴来增加其滚动半径（见图1）。我们预计，这种轴线偏移将降低爬台阶所需的水平力，从而减少用户 effort。此外，由于轮式装置在移动辅助设备中十分常见，本研究的结果可惠及包括老年人和残疾人在内的广泛人群。

助行器、手推车和轮椅等轮式运输装置在日常生活中被广泛使用。这些装置通常在平坦表面上运行，会受到台阶、门槛和凹陷等不平整处的不利影响。轮式装置越过此类不平整处的能力取决于其轮子尺寸相对于不平整处的大小。与在平面上移动相比，攀爬台阶可能需要较大的力。

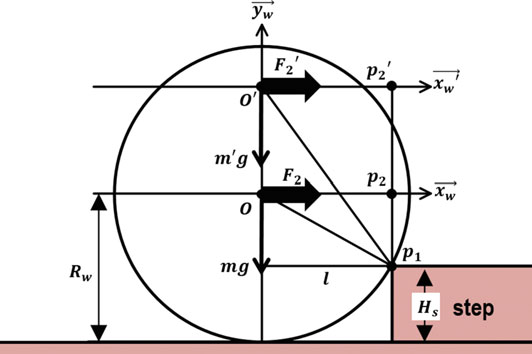
本文考虑了轮子在平面滚动和爬台阶所需的力。假设台阶高度小于车轮半径。如图2所示，轮子的滚动方向定义为 xw，其原点位于O点，绕O点逆时针旋转 90◦得到的轴为 yw，轮子与台阶的接触点记为p1，其在 xw上的法向投影点记为p2。此外，车轮半径定义为Rw，车轮质量为m，重力加速度为 g，滚动摩擦系数为μ。首先，记在平面上移动所需的力为F1。其次，我们计算爬台阶所需的力。爬台阶通过施加在O点的外力与接触点p1处的接触点反作用力形成的力偶产生的顺时针力矩M2（=||p1p2|| ⋅F2）实现。其中，p1到 p2的距离记为||p1p2||。p1与O点之间的水平距离记为l，如图2所示。台阶的高度为 Hs，以便求得 l 为 l= √ 根据勾股定理，R²w −||p1p2||²。为了使轮子能够爬上台阶，外力产生的顺时针力矩必须大于轮子重力产生的逆时针力矩，因此有||p1p2|| ⋅F2 ≥ l ⋅mg。基于此条件表达式，可推导出F2的条件：

$$
||p1p2|| ⋅F2 ≥ \sqrt{R^2_w - ||p1p2||^2} ⋅mg
\implies F2 ≥ \frac{mg}{||p1p2|| \sqrt{R^2_w - ||p1p2||^2}}
\tag{1}
$$

假设轮径和质量分别为100毫米和5千克。根据(1)，对于10、20、30和 40毫米的台阶高度，所需力分别为36.8、65.3、112.3和240.0牛顿。通过这些计算，确认了所需力F2随台阶高度增加而增加。接下来，出于设计目的，比较了100毫米和200毫米轮径在爬台阶时所需的水平力。假设台阶高度为 10毫米，并使用(1)，F2分别求得为36.75和18.85牛顿。

3 轴平移的机构与分析

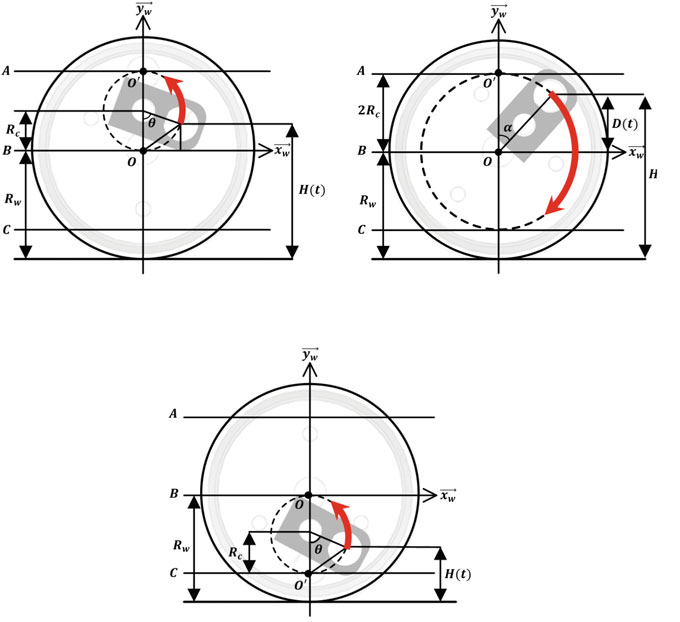
本节介绍了越障台阶所需的旋转轴平移和水平力。图3描述了越障台阶的过程。

依次地，轮子的旋转轴垂直平移，跨越台阶，然后轮子的旋转轴返回其原始位置。图3a和图3c分别显示了轮子旋转轴偏移和恢复的机构。为了便于说明，将运动分为三个独立的运动阶段，对应不同的时间阶段 (k₀ ≤ t < k₁)、(k₁ ≤ t ≤ k₂) 和 (k₂ < t ≤ k₃)。定义曲柄旋转半径为 Rc，在每个时刻 t 轴相对于轮子底部的高度为 H(t)。此处，H(t) 随曲柄和轮子的旋转而变化。特别地，将轴相对于轮子底部处于最高位置处定义为 A，将轴位于轮心位置处定义为 B，将轴相对于轮子底部处于最低位置处定义为 C。

首先，在台阶正前方，轴从轮子的主孔中脱离，曲柄旋转使得轴的末端与辅助孔对齐。随后轴连接到辅助孔上。在此过程中，轮子的旋转轴从O垂直平移至O′，如图3a所示。对于(k₀ ≤ t < k₁)，H(t)作为曲柄转角 θ(t)的函数得出：

$$
H(t) = R_w + R_c - R_c \cos\theta(t)
\tag{2}
$$

其中，H(t)在t = k₀时取最小值B；类似地，在t = k₁时取得最大值A。

其次，我们讨论轮子在爬台阶时的滚动情况。为了越过台阶，轮子分别围绕主孔和辅助孔的中心这两个不同轴旋转。在爬升阶段，我们考虑轮子围绕辅助孔中心的轴旋转的情况。当(k₁ ≤ t ≤ k₂)时，D(t)由D(t) = 2Rc cosα(t)给出，该式是利用图3b中轮子中心与轮子旋转轴之间的连线与 yw所成的角度 α(t)求得的。轴离地面的高度为H(t) = Rw + D(t)。将D(t)代入后可得到以下方程：

$$
H(t) = R_w + 2R_c \cos\alpha(t)
\tag{3}
$$

其中，H(t)在A处且t = k₁时达到最大值。一旦H(t)被移动到A，即执行爬升。爬升完成后，H(t)在高度为C且t = k₂时达到最小值。

第三，我们讨论爬升阶段结束后曲柄对轮子旋转轴的垂直平移。在爬升阶段刚完成时，轴从轮子的辅助孔中脱离，曲柄旋转使轴的一端与主孔对齐，随后轴连接到主孔上。在此过程中，轮子的旋转轴通过垂直平移从O′返回至 O，如图3c所示。由于此时轴已位于轮心位置，可在平面上恢复前进运动。当图(k₂ < t ≤ k₃)3c中时，可推导出H(t)：

$$
H(t) = R_w - R_c - R_c \cos\theta(t)
\tag{4}
$$

4 结果与讨论

在本节中，我们研究了在各种情况下施加到轴上的所需爬楼力。在第2节中，分析了爬台阶所需的水平力。该水平力从轴中心施加到轮子上。实际上，所需的水平力由施加到轮椅后轮的扭矩产生，并通过轮椅车架传递到前轴。通过逐步增加施加的扭矩直至前轮越过台阶，确定了所需的扭矩。此外，针对台阶高度每增加10毫米增量，确定了爬台阶所需的扭矩。图4展示了根据 (1) 和实验测量结果计算出的三种不同情况下的所需力。相同情况的结果也在图4中绘制出来以进行比较。理论分析与实验结果之间具有良好的相关性，这有效验证了所推导方程的正确性。

• 案例 #1 ：160毫米轮径，轴心离地高度为80毫米
• 案例 #2 ：160毫米轮径，轴心离地高度为130毫米
• 案例 #3 ：260毫米轮径，轴心离地高度为130毫米

通过对比案例#1和#3，案例#3的越障爬阶力更小。此外，由于轴高度的原因，案例#3中的轮子能够攀爬更高的台阶。通过比较案例#1和#2，案例#2的越障爬阶力更小。案例#2中的轮子因其轴高度而能够攀爬更高的台阶。此外，对比案例#2和#3表明，案例#2的越障爬阶力更小。在所有台阶高度下，案例#2获得了最小的越障爬阶力。此外，这三个案例的比较还表明，随着台阶高度的增加，各案例之间所需力的差异也随之增大。结果有效地表明，无需使用大轮径即可实现较小的越障爬阶力。

该轮式机构通过改变轴的位置来改变滚动半径。所提出的轴心平移运动根据(1)可使所需爬楼力较小。因此，当轴位于轮心时，轮子可攀爬高度约为其直径31%的台阶。然而，当执行轴心平移运动时，轮子可攀爬高度达其直径约81%的台阶。在当前数学模型下，轮子理论上最高可攀爬至2Rw。但由于所研制的原型受制于可制造性约束，因此实际可攀爬的最大台阶高度受限。

通过使用所提出的机构，能够实现高于Rw的台阶攀爬，这是传统车轮无法做到的。此外，采用小车轮和所提出的机构所需的爬升力远低于相对较大的传统车轮。因此，确认了所提出的机构能够提升轮子攀爬台阶的能力。

该轮式机构设计用于轮椅和手推车。原型已集成到一款商用自走式轮椅中。由于篇幅限制，本文省略了硬件配置和机构的实现细节。有关实际实现的详细信息可参见[7]。实际上，该原型重量约为5千克。通过选用合适的材料和现成部件，有可能设计出更轻便、更紧凑的系统。当前轮式机构仅能从前方向直接攀爬台阶。未来可设计支持从不同方向攀爬台阶的机构。本文使用轮椅进行了实验。在该轮椅上，前方轮子的直径与后轮不同，因此需要考虑后轮爬楼动作。未来还需要考虑使用轮式机构的安全方面。

5 结论

本文提出了一种用于爬台阶的轮式机构。所提出的机构通过垂直偏移轮子的旋转轴来增大其滚动半径，从而增加爬台阶时的伪轮直径。为了验证该轮式机构的有效性和实用性，进行了三种不同情况下的爬楼梯实验。结果表明，在所需越障爬阶力方面，该系统优于直径更大的传统车轮。因此，该机构能够提供更紧凑的系统，并减少用户 effort。未来的研究方向包括减重、安全性的考虑以及使用范围扩展。