奇异值分解（SVD）的应用——图像压缩

SVD方法：模型降阶与图像压缩的应用详解
原创 已于 2024-02-12 11:55:46 修改 · 1.4k 阅读 · 17 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#算法 #矩阵 #模型降阶

于 2024-02-10 20:41:04 首次发布
本文介绍了SVD（奇异值分解）在模型降阶中的应用，包括POD和BT方法，以及如何通过SVD进行图像压缩，如将RGB图像压缩到不同秩，展示了代码示例和图像压缩效果。

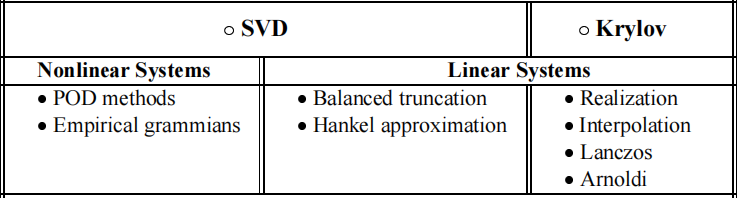
SVD方法是模型降阶的一类重要方法，本征正交分解（POD）和平衡截断（BT）都属于SVD类方法。

要想深入了解模型降阶技术，我们可以先从SVD的应用入手，做一个直观的了解。

1. SVD的定义和分类

我们想寻找一个A的逼近：Ak，使得rank(Ak) = k < n，且|A - Ak|最小。

下面的定理（也称为Schmidt-Mirsky, Eckart-Young定理）说明矩阵A的低秩逼近可以用SVD实现：

最低0.47元/天 解锁文章
【人工智能数学基础篇】——深入详解矩阵分解：奇异值分解（SVD）与主成分分析（PCA）在数据降维与特征提取中的应用
编程技术探索者，分享C/C++、C#、Java、数据库等开发经验，聚焦实战技巧与AI兴趣，助力编程爱好者成长。
12-17 6611
深入详解矩阵分解：奇异值分解（SVD）与主成分分析（PCA）在数据降维与特征提取中的应用
【数学和算法】奇异值分解在【图像压缩】中的应用
u011754972的博客
09-13 2289
图片压缩 比如说，有下面这么一副512x512的图片（方阵才有特征值，所以找了张正方形的图）： 这个图片可以放到一个矩阵里面去，就是把每个像素的颜色值填入到一个512x512的A矩阵中。 根据之前描述的有： 其中， /\是对角阵，对角线上是从大到小排列的特征值。 我们在 /\中
SVD（奇异值分解）应用的python实现（一：图片压缩）
moyao_miao的博客
04-10 2701
当k取奇异值总和的前90%时，可以得到一张与原图几乎一模一样、仅在物体边界处有少量噪点的图片，压缩率为4.97%；注意原始图片为.bmp格式，压缩后的图片为.jpg格式，该图片单纯由.bmp转为.jpg的压缩率为5.07%。当k取奇异值总和的前99%时，可以得到一张与原图一模一样、肉眼无法看出差别的图片，压缩率为5.06%。当k取奇异值总和的前60%时，可以得到一张清晰但有大量噪点的图片，压缩率为4.17%；当k取奇异值总和的前50%时，可以得到一张勉强能够辨认的图片，压缩率为3.41%；
svd图像压缩
09-20
matlab，利用svd算法进行图像压缩。代码主要是利用matlab提供的函数，通过简单的算法实现图像的压缩。压缩率高，同时失真率低，可以很好的实现压缩
《机器学习》—— SVD奇异值分解方法对图像进行压缩
weixin_73504499的博客
09-06 1983
SVD（奇异值分解）是一种在信号处理、统计学、线性代数、机器学习等多个领域广泛应用的矩阵分解方法。它将任何 m×n 矩阵 A 分解为三个特定矩阵的乘积
奇异值分解（SVD）在图像压缩中的应用
最新发布
zbt898241895的博客
12-18 1243
奇异值分解是将一个矩阵分解为三个矩阵的乘积：其中：AA 是一个 m×nm×n 的矩阵。UU 是一个 m×mm×m 的正交矩阵（左奇异向量）。ΣΣ 是一个 m×nm×n 的对角矩阵，对角线上的元素称为奇异值。VTVT 是一个 n×nn×n 的正交矩阵（右奇异向量）。奇异值的大小通常是递减的，较大的奇异值对应矩阵的主要特征，而较小的奇异值则对应噪声或不重要的信息。因此，通过保留较大的奇异值，可以实现数据的降维和压缩。奇异值分解是一种强大的数学工具，能够有效地应用于图像压缩和数据降维。
使用奇异值分解（SVD）压缩图片（python实现）
weixin_62891989的博客
10-22 4135
对3个图层分别进行奇异值分解，可以选取前k个奇异值进行近似表达（每个矩阵的奇异值是唯一的，矩阵大小跟奇异值数量有关），最后合并3个图层就可以以较少的数据表示原图片（也就是使用多于原图片奇异值数量的奇异值可能会使图片更大）。上面的代码显示的图片就是SVD对图片压缩的影响，我们可以看到低奇异值压缩得到的图片会有一些花斑，这些花斑是因为图片的像素亮度差较大造成的，如果我们对图像像素的亮度进行归一化，我们就会得到不错的显示效果。下面是加入归一化的代码。亮的地方变暗，暗的地方变亮。
SVD奇异值分解——矩阵压缩
WL的博客
07-20 867
图片矩阵压缩SVD
奇异值分解SVD及其在矩阵压缩中的应用
在本课程“数学建模13-01 奇异值分解SVD的理论以及对矩阵的压缩”中，重点讲解了SVD的基本理论推导过程，并深入探讨其在矩阵压缩与数据降维中的实际应用价值。 首先，从数学理论上来看，对于任意一个大小为 $ m \...
使用svd分解将图片压缩
m0_56404038的博客
05-15 780
奇异值分解 k=108; I=imread(‘C:\Users\1\Desktop\要做的作业\任务1\Part1\image.jpg’); h=size(I,1); w=size(I,2); R=I(:,:,1); G=I(:,:,2); B=I(:,:,3); Rd=im2double®; Gd=im2double(G); Bb=im2double(B);%转换为双精度 [Ur,Sr,Vr]=svd(Rd);%svd分解 [Ug,Sg,Vg]=svd(Gd); [Ub,Sb,Vb]=svd(Bb); R
SVD图像压缩
10-19
利用SVD分解师实现图像压缩，Python实现。奇异值数目暂定60，可更改
机器学习实战：用SVD压缩图像
04-17 5053
前文我们了解了奇异值分解（SVD）的原理，今天就实战一下，用矩阵的奇异值分解对图片进行压缩. Learn by doing 我做了一个在线的图像压缩应用，大家可以感受一下。 https://huggingface.co/spaces/beihai/Image-Compression-with-SVD 功能很简单，上传需要压缩的图片，选择压缩比，提交即可。 下面咱们就一起看看实现过程 用SVD压缩图像 原理很简单： 将图片分解为RGB三颜色矩阵，将每个颜色矩阵进行奇异值分解，然后
图像压缩之奇异值分解（SVD）
AIGC Studio：分享AIGC前沿知识和好玩应用，公众号同名。
07-31 6889
最近有点时间把之前研究的图像压缩相关内容做以下记录和总结，包括一些经典方法代码实现以及原理介绍。 首先直接上Lena女神原图照片。 对于SVD分解来说，选取不同的奇异值数量压缩倍数也不一样，简单理解就是选取的奇异值数量越多压缩倍数越小，反之越大，SVD的缺点就是以牺牲图像细节信息来达到图像压缩的目的。这也是为什么奇异值分解的图像压缩方法没有像DCT，小波变换一样成为JPEG压缩的标准吧。下面针对以下数据做一定实验，通过选取奇异值数量k为10,20,30,40来分别看一下图像压缩效果,如何能在尽量少舍
利用SVD进行图像压缩
weixin_36600799的博客
04-25 2048
利用SVD进行图像压缩 前边一篇文章中，总结了SVD相关的理论支持，老是一味的搞理论没有实践毕竟也是不行的，所以本文会简单的实现一个基于Python的图像压缩示例程序，来使用SVD进行简单图片的压缩以及还原实验。 首先来看代码，完整的代码如下： # -*- coding: utf-8 -*- import argparse import os import cv2 import numpy a...
奇异值分解在图像压缩中的应用（有MATLAB仿真程序）
MaoChuangAn的博客
06-16 4053
这篇文章其实也是矩阵分析的一个作业，当时也是矩阵奇异值分解挺有意思的，所以就在网上查找奇异值分解的相关应用。自己对图像处理也很感兴趣，因此就选择了图像压缩这个应用。写博客是个很好的学习方法，坚持写博客也是一个好习惯。下面就直接把论文贴上来。附录1：奇异值分解几何意义程序t=[0:0.01:2*pi]; x=cos(t);y=sin(t);%变换矩阵A = [1 -2;1 2];A = double...
SVD在图像压缩中的应用
weixin_44345862的博客
11-30 557
奇异值可以看作是一个矩阵的代表值，奇异值越多越大时，代表信息越多，奇异值排列后，可以取前面若干大的的奇异值可以基本还原数据本身。可以看到，当我们取到前面120个奇异值来重构图片时，基本上已经看不出与原图片有多大的差别。奇异值下降很快，取前面几个大的奇异值，可以基本还原矩阵信息。下面的代码运行环境为。
【图像压缩】基于奇异值分解SVD实现图像压缩附Matlab代码
m0_60703264的博客
03-05 1330
图像压缩是图像处理中一项重要的技术，它可以减少图像文件的大小，便于存储和传输。目前，图像压缩算法主要分为有损压缩和无损压缩两大类。有损压缩算法可以获得更高的压缩比，但会损失部分图像信息；而无损压缩算法则可以保证图像信息不丢失，但压缩比相对较低。本文将介绍一种基于奇异值分解（SVD）的图像有损压缩算法。SVD是一种矩阵分解技术，可以将一个矩阵分解为三个矩阵的乘积，即 U、Σ 和 V。
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值