leetcode44 ---通配符匹配----DP

超时解法：：：疯狂重复计算 

bool isMatch(string s, string p) {
	if (p.empty())
		return s.empty();
	if (s.empty()) {
		for (int i = 0; i < p.length(); i++)
			if (p[i] != '*')
				return false;
		return true;
	}
	if (s[0] != p[0] && p[0] != '?'&&p[0] != '*')
		return false;
	if (s[0] == p[0]||p[0]=='?')
		return isMatch(s.substr(1), p.substr(1));
	if (p[0] == '*')
		return isMatch(s, p.substr(1)) || isMatch(s.substr(1), p); //超时
}

众所周知，DP最难的地方在于找出有递推式的模型。。。

我们这么来思考这个问题，假设我们知道匹配字符串s="abcde"与字符串p是否匹配;

那么我们如果在p后面再加一个字母会怎么样呢？

这时我们要很自然的想到-----根据加入的字符分类

1---加入字符为‘*’，那么这个‘*’可以匹配0个或者多个字符，

如果匹配0个，那么就等价于s与p是否匹配了；如果匹配1个，那么就等价于s="abcd" 与p是否匹配了；那么你会问了，如果匹配2个，3个呢？这个问题可以划归为   将匹配大于等于1次，那么就等价于 s="abcd"与（p+‘*‘’）是否匹配了。-------这里很精妙

其实很多问题都是这样，分为 0,1,2,3,4这种，我们往往可以划归成0,1问题；想想一颗二叉树。

我们就可以把问题简化了。。这种思想很重要，常常用到，好好体会吧。
如果用dp[x][y]表示s前x个字符和p的前y个字符匹配的结果。。
那么我们上述分析的结果用数学表达式表示就是
when p[y-1]='*';
dp[x][y]=dp[x][y-1]||dp[x-1][y];

2---如果加入字符为'?'呢？
when p[y-1]='?'
dp[x][y]=dp[x-1][y-1];

3---最后一种情况如果都不是呢？(这里s[-1]表示最后一个字符)
when p[y-1]!='?'&&p[y-1]!='*'
dp[x][y]=s[-1]==p[-1]?dp[x-1][y-1]:false;

我们这里就完成了动态规划的建模部分。


BUT  动态规划中还有一个非常重要的东西-----what do you know at first???也就是边界问题。。

就像递归，我们首先得知道一些初始值吧，不然递归到最后谁买单啊？？

红色部分就是边界，我们往往要单独处理。而这些部分也是非常简单的。

     

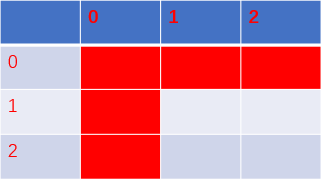
当x=0时，当且仅当p全为*才为true;

当y为0时，那还匹配个毛线，全为false,(最开始赋初值时候就已经全为false了，所以这个不用单独处理)

最后还有dp[0][0]=true;

 

分析这么多了，剩下的自由发挥吧-----可以看看https://leetcode-cn.com/problems/wildcard-matching/comments/85993；

我觉得写得很不错，回溯法解决的那个答案我得再看看。。。